2022年新教材高中数学第一章集合与常用逻辑用语1.2集合的基本关系课件新人教B版必修第一册 课件(共19张PPT)
文档属性
| 名称 | 2022年新教材高中数学第一章集合与常用逻辑用语1.2集合的基本关系课件新人教B版必修第一册 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 412.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:18:30 | ||
图片预览




文档简介
(共19张PPT)
1.1.2 集合的基本关系
1.能识别给定集合的子集,理解子集、真子集的概念.
2.理解集合相等的含义,会用子集的观点来解释两个集合相等.
3.在具体情境中了解空集的含义,并理解空集是任何集合的子集.
4.初步认识维恩图,并会用维恩图来表示两个集合的关系,能借助集合间的关系与
特征来研究有关集合的问题.
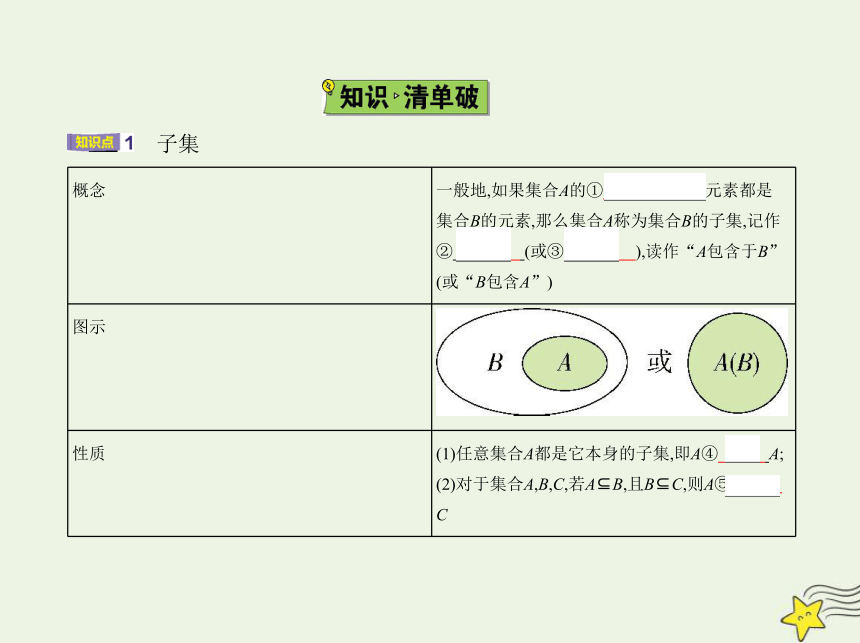
概念 一般地,如果集合A的① 任意一个 元素都是
集合B的元素,那么集合A称为集合B的子集,记作
② A B (或③ B A ),读作“A包含于B”
(或“B包含A”)
图示
性质 (1)任意集合A都是它本身的子集,即A④ A;
(2)对于集合A,B,C,若A B,且B C,则A⑤
C
子集
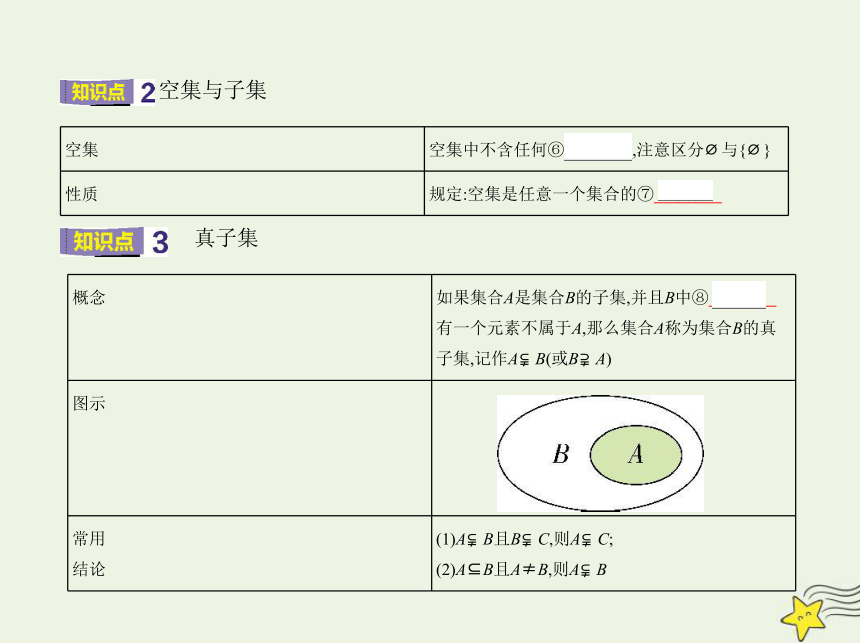
空集与子集
空集 空集中不含任何⑥ 元素 ,注意区分 与{ }
性质 规定:空集是任意一个集合的⑦ 子集
真子集
概念 如果集合A是集合B的子集,并且B中⑧ 至少
有一个元素不属于A,那么集合A称为集合B的真
子集,记作A B(或B A)
图示
常用 结论 (1)A B且B C,则A C;
(2)A B且A≠B,则A B
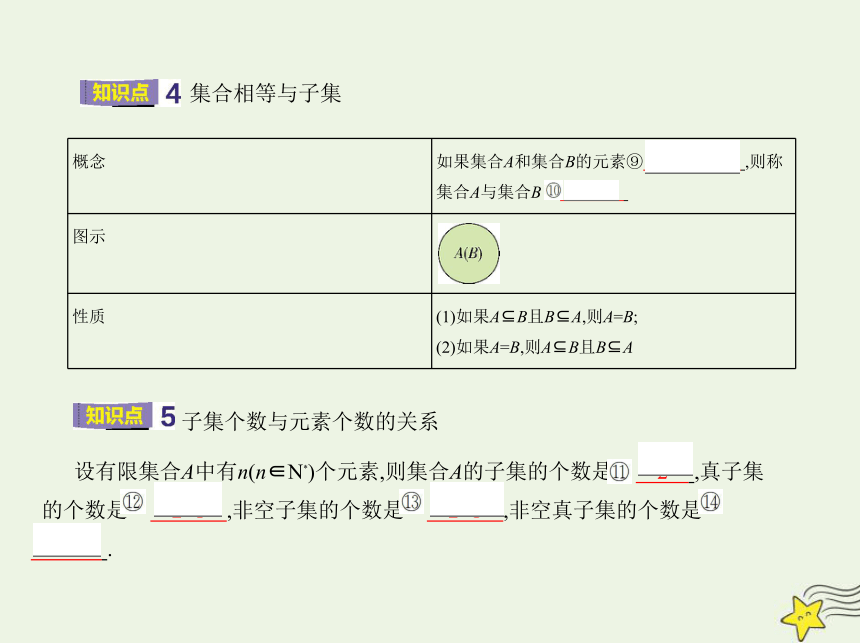
集合相等与子集
子集个数与元素个数的关系
设有限集合A中有n(n∈N*)个元素,则集合A的子集的个数是 2n ,真子集
的个数是 2n-1 ,非空子集的个数是 2n-1 ,非空真子集的个数是
2n-2 .
概念 如果集合A和集合B的元素⑨ 完全相同 ,则称
集合A与集合B 相等
图示
性质 (1)如果A B且B A,则A=B;
(2)如果A=B,则A B且B A
判断正误,正确的画“√”,错误的画“ ”.
1.育才中学高一(3)班所有学生组成集合A,所有女生组成集合B,参加秋季运动会
的运动员组成集合C,则B A且C B. ( )
2.任何一个集合都有子集和真子集. ( )
3.{0,1,2} {0,1,2,3}. ( √ )
4.集合M={x|x≤ },a= ,则a M.( )
5.已知集合B A,若a A,则a B. ( √ )
6.集合A={x|x2-x=0},B={0,1},则A=B. ( √ )
已知集合A={x|x=1},B={x|x2-3x+2=0}.
问题
1.判断集合A与集合B间的关系.
提示:易得B={1,2},由于集合A中的元素都在集合B中,但集合B中的元素2不在集
合A中,因此A B.
2.若集合A={x|x>1},B={x|x2-3x+2>0},如何判断集合A与B的关系
提示:解不等式,利用数轴判断.
集合间关系的判断
判断集合间关系的方法
1.列举法:对于能列举的集合,用列举法将两个集合表示出来,再通过比较两集合
中的元素来判断.
2.元素特征法:弄清集合中元素的共同特征,再利用各集中元素的共同特征之间的
关系来判断集合间的关系.即:若集合A中的任一元素都满足集合B中元素的共同
特征,则A是B的子集,否则A不是B的子集;同理可判断B是不是A的子集.
3.图示法:利用数轴或维恩图表示集合,可直观地判断两集合之间的关系.
拔高问题
3.集合M= ,N= ,请阐述判断M,N之间关系的方法.
提示:利用列举法或元素特征法判断.
破疑典例
1.( )已知A={x|y= ,y≥0},B={y|y= ,x≥0},有下列说法:
①A B;②A=B;③A B.其中,正确说法的个数是 ( )
A.1 B.2 C.3 D.0
思路点拨:
确定集合A中元素x的取值范围 确定集合B中元素y的取值范围 确定
集合A与B之间的关系,得出结论.
B 由已知得,集合A中x≥0,集合B中y≥0,所以A=B,A B,①②正确,③不正确.故
选B.
2.( )已知集合M= x x=m+ ,m∈Z ,N= x x= - ,n∈Z ,P= x x= + ,
k∈Z .试确定集合M、N、P之间的关系.
思路点拨:
分析集合M、N、P中元素的性质特征 判断M、N、P之间的关系.
解析 解法一:
∵M= ,
N=
= x x= - 或x= - ,p∈Z
= x x=p- 或x=p+ ,p∈Z ,
P=
= x x= + 或x= + ,t∈Z
= ,
∴M N=P.
解法二:
∵M=
=
= ,
N=
=
= ,
P=
= ,
∴M N=P.
已知集合A={3,1},B={m,1},若两集合A、B相等,则可由集合间的关系得到集合的
元素之间的关系,进而可以求相关参数的值或取值范围,当集合中的元素已知时,
可用列举法解决问题.
问题
1.已知集合A={2,-1},B={m2-m,-1},若A=B,如何求实数m的值
提示:由A=B得m2-m=2,
即m2-m-2=0,
解得m=2或m=-1.
已知集合间关系求参数的值(取值范围)
2.已知集合A={x|1≤x≤2},集合B={x|1≤x≤a,a≥1},若A B,如何求a的取值范围
提示:若A B,画出数轴:
由数轴可知a>2.
3.在问题2中,将“A B”改为“B A”,又如何求a的取值范围
提示:若B A,画出数轴:
由图可知1≤a≤2.
由集合间的关系求参数问题的注意点及常用方法
1.注意点:
(1)不能忽视集合为 的情形;
(2)当集合中含有参数时,一般需要分类讨论.
2.常用方法:对于用不等式描述的集合,已知集合的包含关系求相关参数的值(取
值范围)时,常采用数形结合的思想,借助数轴来解答.
拔高问题
4.已知集合A={x|-3≤x≤4},B={x|2m-1围
提示:当B= 时,m+1≤2m-1,
解得m≥2;
当B≠ 时,有
解得-1≤m<2.
综上,m≥-1.
破疑典例
1.( )已知集合A={x|1思路点拨:
分别求出当a>0,a=0,a<0时的集合A,再根据集合A、B之间的关系,利用数轴
求出实数a的取值范围.
解析 ①当a=0时,A= ,满足A B.
②当a>0时,A= ,
由B={x|-1可画出数轴:
∴ ∴a≥2.
③当a<0时,A= ,
由B={x|-1可画出数轴:
∴ ∴a≤-2.
综上所述,a的取值范围是{a|a=0或a≥2或a≤-2}.
陷阱分析 解题时注意空集是任何集合的子集这一特殊情况,防止漏解(如本题中a=0满足题意).
2.( )设集合A={x|x2+x-6=0},B={x|mx+1=0},若B A,求实数m的值所组成的集
合.
思路点拨:
用列举法表示集合A,由B A,对B进行分类讨论,计算得m的值.
解析 A={x|x2+x-6=0}={-3,2}.由B A,且B中最多只有一个元素,得B= 或B={-3}
或B={2}.
当m=0时,mx+1=0无解,故B= ,满足条件;
当B={-3}时,-3m+1=0,解得m= ;
当B={2}时,2m+1=0,解得m=- .
故满足条件的实数m所组成的集合为 .
1.1.2 集合的基本关系
1.能识别给定集合的子集,理解子集、真子集的概念.
2.理解集合相等的含义,会用子集的观点来解释两个集合相等.
3.在具体情境中了解空集的含义,并理解空集是任何集合的子集.
4.初步认识维恩图,并会用维恩图来表示两个集合的关系,能借助集合间的关系与
特征来研究有关集合的问题.
概念 一般地,如果集合A的① 任意一个 元素都是
集合B的元素,那么集合A称为集合B的子集,记作
② A B (或③ B A ),读作“A包含于B”
(或“B包含A”)
图示
性质 (1)任意集合A都是它本身的子集,即A④ A;
(2)对于集合A,B,C,若A B,且B C,则A⑤
C
子集
空集与子集
空集 空集中不含任何⑥ 元素 ,注意区分 与{ }
性质 规定:空集是任意一个集合的⑦ 子集
真子集
概念 如果集合A是集合B的子集,并且B中⑧ 至少
有一个元素不属于A,那么集合A称为集合B的真
子集,记作A B(或B A)
图示
常用 结论 (1)A B且B C,则A C;
(2)A B且A≠B,则A B
集合相等与子集
子集个数与元素个数的关系
设有限集合A中有n(n∈N*)个元素,则集合A的子集的个数是 2n ,真子集
的个数是 2n-1 ,非空子集的个数是 2n-1 ,非空真子集的个数是
2n-2 .
概念 如果集合A和集合B的元素⑨ 完全相同 ,则称
集合A与集合B 相等
图示
性质 (1)如果A B且B A,则A=B;
(2)如果A=B,则A B且B A
判断正误,正确的画“√”,错误的画“ ”.
1.育才中学高一(3)班所有学生组成集合A,所有女生组成集合B,参加秋季运动会
的运动员组成集合C,则B A且C B. ( )
2.任何一个集合都有子集和真子集. ( )
3.{0,1,2} {0,1,2,3}. ( √ )
4.集合M={x|x≤ },a= ,则a M.( )
5.已知集合B A,若a A,则a B. ( √ )
6.集合A={x|x2-x=0},B={0,1},则A=B. ( √ )
已知集合A={x|x=1},B={x|x2-3x+2=0}.
问题
1.判断集合A与集合B间的关系.
提示:易得B={1,2},由于集合A中的元素都在集合B中,但集合B中的元素2不在集
合A中,因此A B.
2.若集合A={x|x>1},B={x|x2-3x+2>0},如何判断集合A与B的关系
提示:解不等式,利用数轴判断.
集合间关系的判断
判断集合间关系的方法
1.列举法:对于能列举的集合,用列举法将两个集合表示出来,再通过比较两集合
中的元素来判断.
2.元素特征法:弄清集合中元素的共同特征,再利用各集中元素的共同特征之间的
关系来判断集合间的关系.即:若集合A中的任一元素都满足集合B中元素的共同
特征,则A是B的子集,否则A不是B的子集;同理可判断B是不是A的子集.
3.图示法:利用数轴或维恩图表示集合,可直观地判断两集合之间的关系.
拔高问题
3.集合M= ,N= ,请阐述判断M,N之间关系的方法.
提示:利用列举法或元素特征法判断.
破疑典例
1.( )已知A={x|y= ,y≥0},B={y|y= ,x≥0},有下列说法:
①A B;②A=B;③A B.其中,正确说法的个数是 ( )
A.1 B.2 C.3 D.0
思路点拨:
确定集合A中元素x的取值范围 确定集合B中元素y的取值范围 确定
集合A与B之间的关系,得出结论.
B 由已知得,集合A中x≥0,集合B中y≥0,所以A=B,A B,①②正确,③不正确.故
选B.
2.( )已知集合M= x x=m+ ,m∈Z ,N= x x= - ,n∈Z ,P= x x= + ,
k∈Z .试确定集合M、N、P之间的关系.
思路点拨:
分析集合M、N、P中元素的性质特征 判断M、N、P之间的关系.
解析 解法一:
∵M= ,
N=
= x x= - 或x= - ,p∈Z
= x x=p- 或x=p+ ,p∈Z ,
P=
= x x= + 或x= + ,t∈Z
= ,
∴M N=P.
解法二:
∵M=
=
= ,
N=
=
= ,
P=
= ,
∴M N=P.
已知集合A={3,1},B={m,1},若两集合A、B相等,则可由集合间的关系得到集合的
元素之间的关系,进而可以求相关参数的值或取值范围,当集合中的元素已知时,
可用列举法解决问题.
问题
1.已知集合A={2,-1},B={m2-m,-1},若A=B,如何求实数m的值
提示:由A=B得m2-m=2,
即m2-m-2=0,
解得m=2或m=-1.
已知集合间关系求参数的值(取值范围)
2.已知集合A={x|1≤x≤2},集合B={x|1≤x≤a,a≥1},若A B,如何求a的取值范围
提示:若A B,画出数轴:
由数轴可知a>2.
3.在问题2中,将“A B”改为“B A”,又如何求a的取值范围
提示:若B A,画出数轴:
由图可知1≤a≤2.
由集合间的关系求参数问题的注意点及常用方法
1.注意点:
(1)不能忽视集合为 的情形;
(2)当集合中含有参数时,一般需要分类讨论.
2.常用方法:对于用不等式描述的集合,已知集合的包含关系求相关参数的值(取
值范围)时,常采用数形结合的思想,借助数轴来解答.
拔高问题
4.已知集合A={x|-3≤x≤4},B={x|2m-1
提示:当B= 时,m+1≤2m-1,
解得m≥2;
当B≠ 时,有
解得-1≤m<2.
综上,m≥-1.
破疑典例
1.( )已知集合A={x|1
分别求出当a>0,a=0,a<0时的集合A,再根据集合A、B之间的关系,利用数轴
求出实数a的取值范围.
解析 ①当a=0时,A= ,满足A B.
②当a>0时,A= ,
由B={x|-1
∴ ∴a≥2.
③当a<0时,A= ,
由B={x|-1
∴ ∴a≤-2.
综上所述,a的取值范围是{a|a=0或a≥2或a≤-2}.
陷阱分析 解题时注意空集是任何集合的子集这一特殊情况,防止漏解(如本题中a=0满足题意).
2.( )设集合A={x|x2+x-6=0},B={x|mx+1=0},若B A,求实数m的值所组成的集
合.
思路点拨:
用列举法表示集合A,由B A,对B进行分类讨论,计算得m的值.
解析 A={x|x2+x-6=0}={-3,2}.由B A,且B中最多只有一个元素,得B= 或B={-3}
或B={2}.
当m=0时,mx+1=0无解,故B= ,满足条件;
当B={-3}时,-3m+1=0,解得m= ;
当B={2}时,2m+1=0,解得m=- .
故满足条件的实数m所组成的集合为 .
