2021-2022学年湘教版九年级数学下册2.4 过不共线三点作圆 同步练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册2.4 过不共线三点作圆 同步练习 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 10:51:59 | ||
图片预览




文档简介
2.4 过不共线三点作圆
一、选择题
1.可以作圆且只可作一个圆的条件是( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过直线上两点和该直线外一点
2.小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在如图1所示的玻璃镜残片的边缘描出了点A,B,C,得到三角形ABC,则这块玻璃镜的圆心是( )
图1
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
3.三角形的外心是( )
A.三角形三条角平分线的交点
B.三角形三条边的垂直平分线的交点
C.三角形三条高的交点
D.三角形三条中线的交点
4.已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
A.40° B.60° C.80° D.100°
5 如图3,☉O是△ABC的外接圆,半径为2 cm,若BC=2 cm,则∠A的度数为
( )
图3
A.30° B.25° C.15° D.10°
6 如图4,在△ABC中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则△ABC外接圆的面积为( )
图4
A.3π B.4π C.6π D.9π
7 有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A的度数.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图7,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑得不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
图7
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A的值就是65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
8.如图8,AB=OA=OB=OC,则∠ACB的大小是( )
图8
A.40° B.30° C.20° D.35°
9.[2020·陕西] 如图9,△ABC内接于☉O,∠A=50°.E是边BC的中点,连接OE并延长,交☉O于点D,连接BD,则∠D的大小为( )
图9
A.55° B.65° C.60° D.75°
填空题
10 如图5,AD是△ABC的外接圆☉O的直径,若∠BCA=50°,则∠ADB= °.
图5
11如图10,方格纸上每个小正方形的边长均为1个单位,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
图10
12 如图11,已知锐角三角形ABC内接于半径为2的☉O,OD⊥BC于点D,∠BAC=60°,则OD= .
图11
解答题
13.小明家的房前有一块空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明在图2中把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
图2
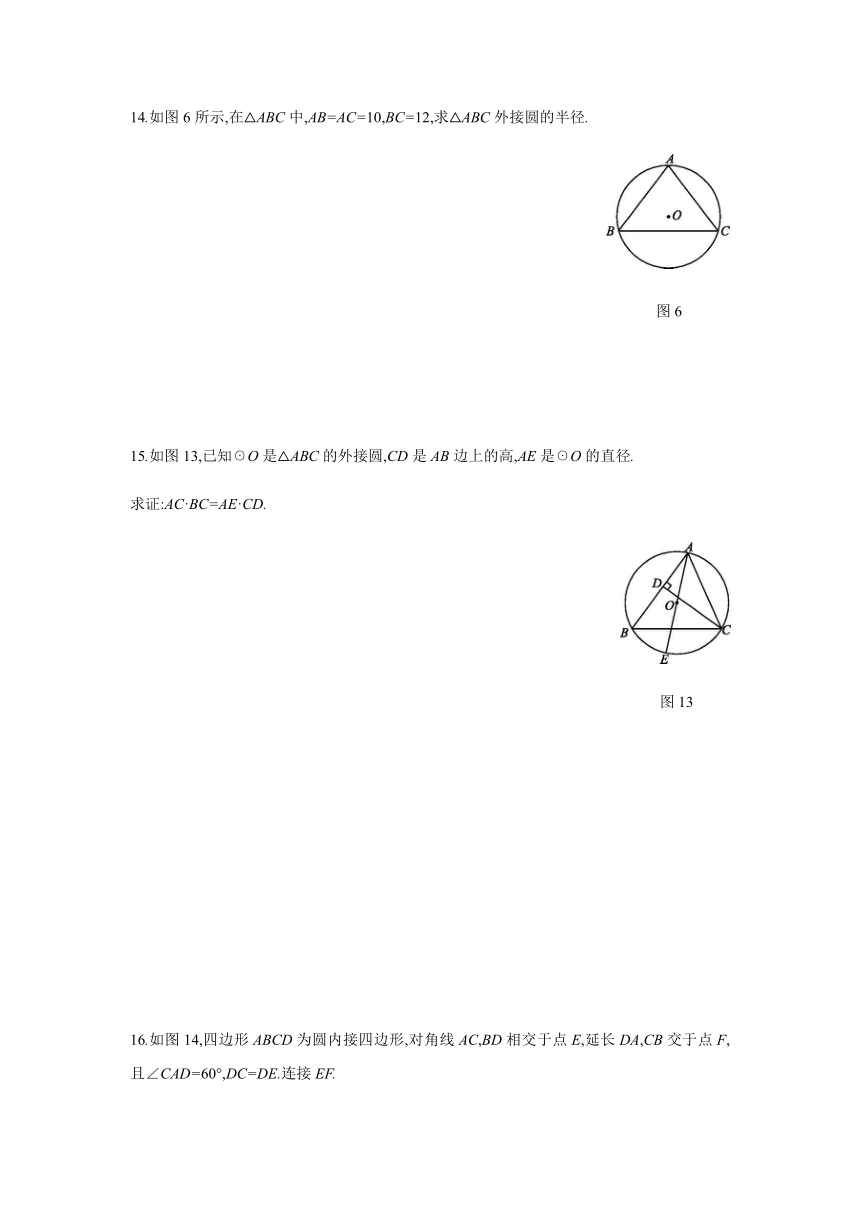
14.如图6所示,在△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
图6
15.如图13,已知☉O是△ABC的外接圆,CD是AB边上的高,AE是☉O的直径.
求证:AC·BC=AE·CD.
图13
16.如图14,四边形ABCD为圆内接四边形,对角线AC,BD相交于点E,延长DA,CB交于点F,且∠CAD=60°,DC=DE.连接EF.
求证:(1)AB=AF;
(2)A为△BEF的外心(即△BEF外接圆的圆心).
图14
2.4 过不共线三点作圆
1.D
2.B
3.B
4.C
5.A
6.D
7.A
8.B
9.B
10.50
11(-1,-2)
12.1
13.解:如图,过点A作AD⊥BC于点D,连接OB.
∵AB=AC,
∴AD垂直平分线段BC,且外心O在AD上,
∴BD=BC=6.
在Rt△ABD中,AD==8.
设OA=OB=r,
在Rt△OBD中,OB2=OD2+BD2,
即r2=(8-r)2+62,解得r=.
即△ABC外接圆的半径为.
14.解:(1)如图,☉O即为所求.
(2)如图,连接OB,设线段BC的垂直平分线交BC于点E.
由题意,得OE=4,BE=EC=BC=3.
在Rt△OBE中,OB==5,
∴S☉O=π×52=25π.
故答案为25π.
15.证明:如图,连接EC,
∵∠B,∠E都是所对的圆周角,
∴∠B=∠E.
∵AE是☉O的直径,∴∠ACE=90°.
∵CD是AB边上的高,
∴∠CDB=90°.
在△AEC和△CBD中,
∵∠E=∠B,∠ACE=∠CDB,
∴△AEC∽△CBD,
∴=.
即AC·BC=AE·CD.
16.证明:(1)∵DC=DE,∴∠ACD=∠DEC.
∵∠CAD=60°,∴∠ABF=∠ADC=120°-∠ACD=120°-∠DEC=120°-(60°+∠ADE)=60°-∠ADE,
而∠F=∠CAD-∠ACF=60°-∠ACF,∠ACF=∠ADE,
∴∠ABF=∠F,∴AB=AF.
(2)∵四边形ABCD内接于圆,
∴∠ABD=∠ACD.
又DC=DE,
∴∠DCE=∠DEC=∠AEB,
∴∠ABD=∠AEB,
∴AB=AE.
∴AB=AF=AE,
即A为△BEF的外心.
一、选择题
1.可以作圆且只可作一个圆的条件是( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过直线上两点和该直线外一点
2.小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在如图1所示的玻璃镜残片的边缘描出了点A,B,C,得到三角形ABC,则这块玻璃镜的圆心是( )
图1
A.AB,AC边上的中线的交点
B.AB,AC边的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
3.三角形的外心是( )
A.三角形三条角平分线的交点
B.三角形三条边的垂直平分线的交点
C.三角形三条高的交点
D.三角形三条中线的交点
4.已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
A.40° B.60° C.80° D.100°
5 如图3,☉O是△ABC的外接圆,半径为2 cm,若BC=2 cm,则∠A的度数为
( )
图3
A.30° B.25° C.15° D.10°
6 如图4,在△ABC中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则△ABC外接圆的面积为( )
图4
A.3π B.4π C.6π D.9π
7 有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A的度数.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图7,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑得不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
图7
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A的值就是65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
8.如图8,AB=OA=OB=OC,则∠ACB的大小是( )
图8
A.40° B.30° C.20° D.35°
9.[2020·陕西] 如图9,△ABC内接于☉O,∠A=50°.E是边BC的中点,连接OE并延长,交☉O于点D,连接BD,则∠D的大小为( )
图9
A.55° B.65° C.60° D.75°
填空题
10 如图5,AD是△ABC的外接圆☉O的直径,若∠BCA=50°,则∠ADB= °.
图5
11如图10,方格纸上每个小正方形的边长均为1个单位,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
图10
12 如图11,已知锐角三角形ABC内接于半径为2的☉O,OD⊥BC于点D,∠BAC=60°,则OD= .
图11
解答题
13.小明家的房前有一块空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明在图2中把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
图2
14.如图6所示,在△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
图6
15.如图13,已知☉O是△ABC的外接圆,CD是AB边上的高,AE是☉O的直径.
求证:AC·BC=AE·CD.
图13
16.如图14,四边形ABCD为圆内接四边形,对角线AC,BD相交于点E,延长DA,CB交于点F,且∠CAD=60°,DC=DE.连接EF.
求证:(1)AB=AF;
(2)A为△BEF的外心(即△BEF外接圆的圆心).
图14
2.4 过不共线三点作圆
1.D
2.B
3.B
4.C
5.A
6.D
7.A
8.B
9.B
10.50
11(-1,-2)
12.1
13.解:如图,过点A作AD⊥BC于点D,连接OB.
∵AB=AC,
∴AD垂直平分线段BC,且外心O在AD上,
∴BD=BC=6.
在Rt△ABD中,AD==8.
设OA=OB=r,
在Rt△OBD中,OB2=OD2+BD2,
即r2=(8-r)2+62,解得r=.
即△ABC外接圆的半径为.
14.解:(1)如图,☉O即为所求.
(2)如图,连接OB,设线段BC的垂直平分线交BC于点E.
由题意,得OE=4,BE=EC=BC=3.
在Rt△OBE中,OB==5,
∴S☉O=π×52=25π.
故答案为25π.
15.证明:如图,连接EC,
∵∠B,∠E都是所对的圆周角,
∴∠B=∠E.
∵AE是☉O的直径,∴∠ACE=90°.
∵CD是AB边上的高,
∴∠CDB=90°.
在△AEC和△CBD中,
∵∠E=∠B,∠ACE=∠CDB,
∴△AEC∽△CBD,
∴=.
即AC·BC=AE·CD.
16.证明:(1)∵DC=DE,∴∠ACD=∠DEC.
∵∠CAD=60°,∴∠ABF=∠ADC=120°-∠ACD=120°-∠DEC=120°-(60°+∠ADE)=60°-∠ADE,
而∠F=∠CAD-∠ACF=60°-∠ACF,∠ACF=∠ADE,
∴∠ABF=∠F,∴AB=AF.
(2)∵四边形ABCD内接于圆,
∴∠ABD=∠ACD.
又DC=DE,
∴∠DCE=∠DEC=∠AEB,
∴∠ABD=∠AEB,
∴AB=AE.
∴AB=AF=AE,
即A为△BEF的外心.
