第三章圆单元检测题2021-2022学年北师大版九年级下册数学(word版含答案)
文档属性
| 名称 | 第三章圆单元检测题2021-2022学年北师大版九年级下册数学(word版含答案) | 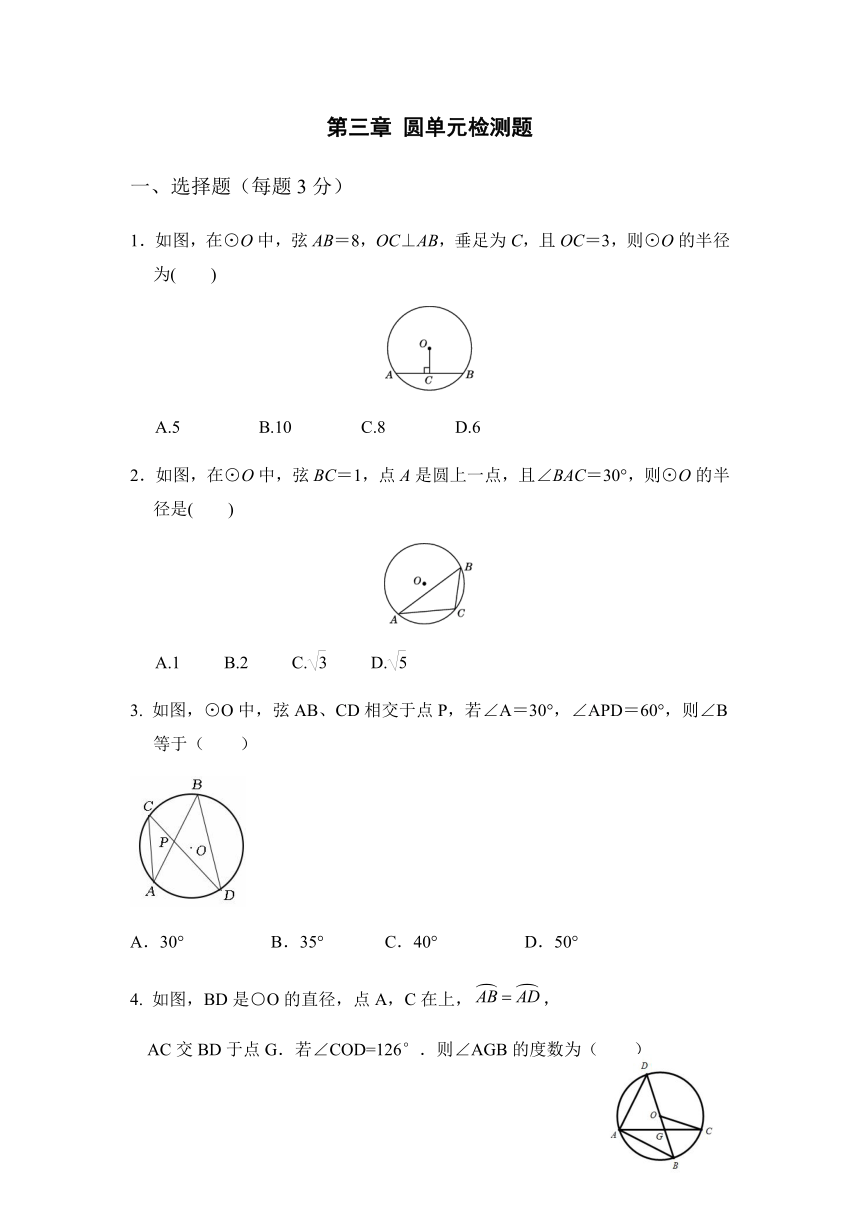 | |
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 10:56:37 | ||
图片预览


文档简介
第三章 圆单元检测题
一、选择题(每题3分)
1.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5 B.10 C.8 D.6
2.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )
A.1 B.2 C. D.
如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=60°,则∠B等于( )
A.30° B.35° C.40° D.50°
如图,BD是○O的直径,点A,C在上,,
AC交BD于点G.若∠COD=126°.则∠AGB的度数为( )
99° B.108°
110° D.117°
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
π B.2π C.3π D.4π
6. 如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.22 B.3 C.4 D.2
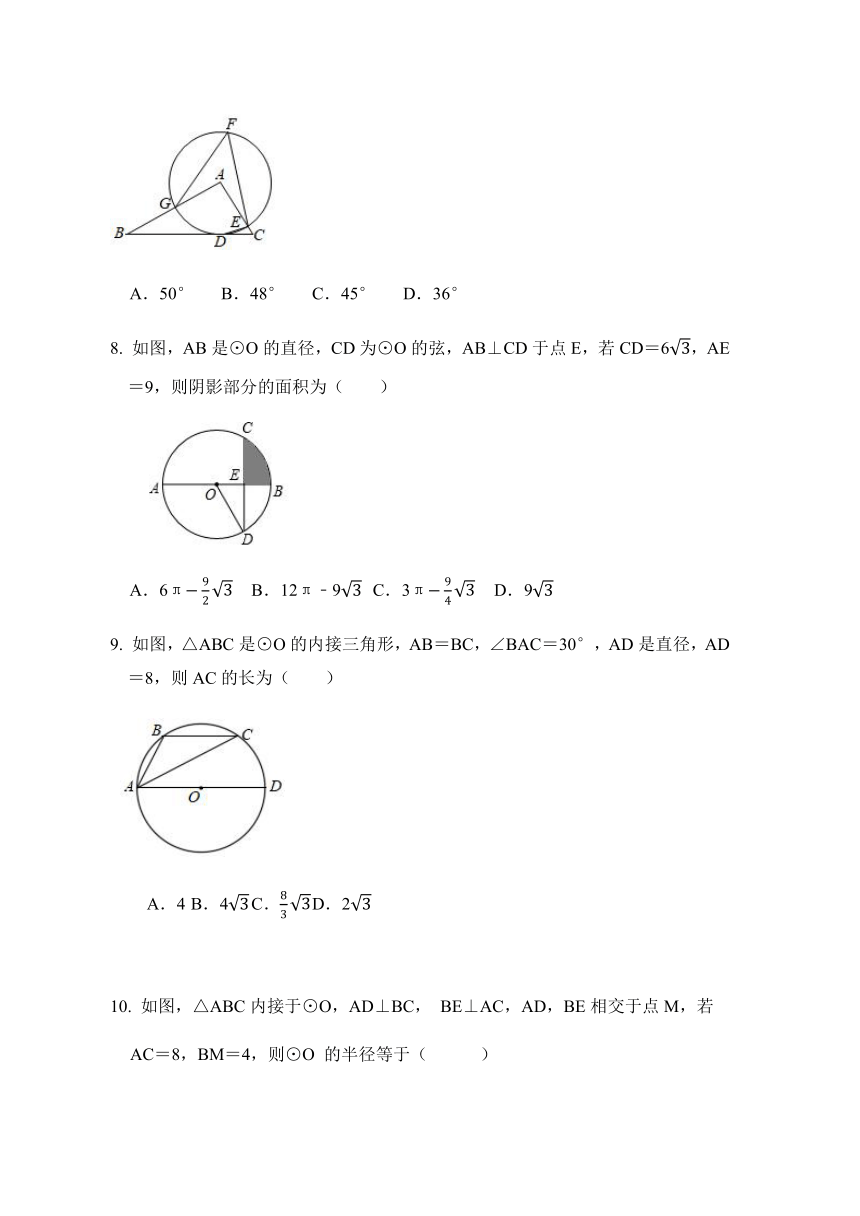
7.如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
如图,AB是⊙O的直径,CD为⊙O的弦,AB⊥CD于点E,若CD=6,AE=9,则阴影部分的面积为( )
A.6π B.12π﹣9 C.3π D.9
如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
如图,△ABC内接于⊙O,AD⊥BC, BE⊥AC,AD,BE相交于点M,若
AC=8,BM=4,则⊙O 的半径等于( )
A. B. C. D.6
二、填空题(每题4分)
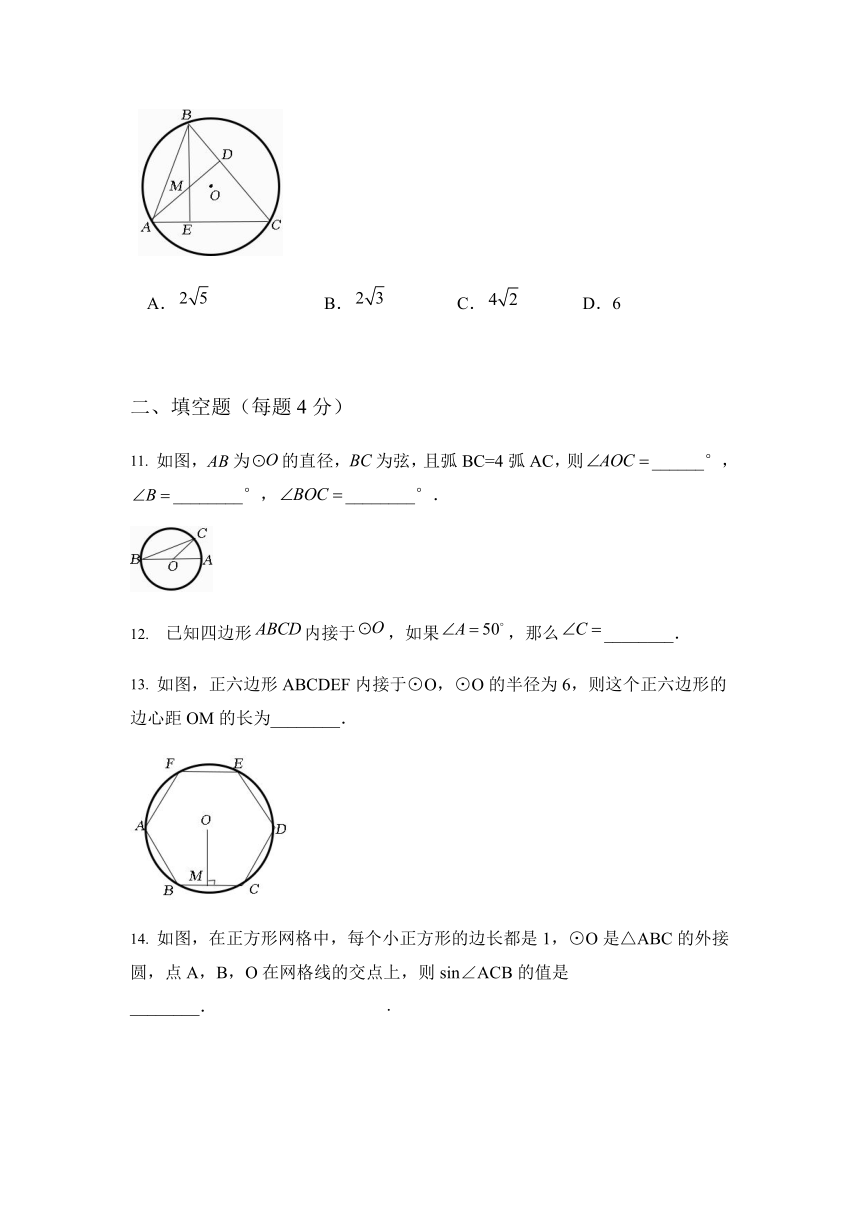
11. 如图,为的直径,为弦,且弧BC=4弧AC,则______°,________°,________°.
12. 已知四边形内接于,如果,那么________.
13. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
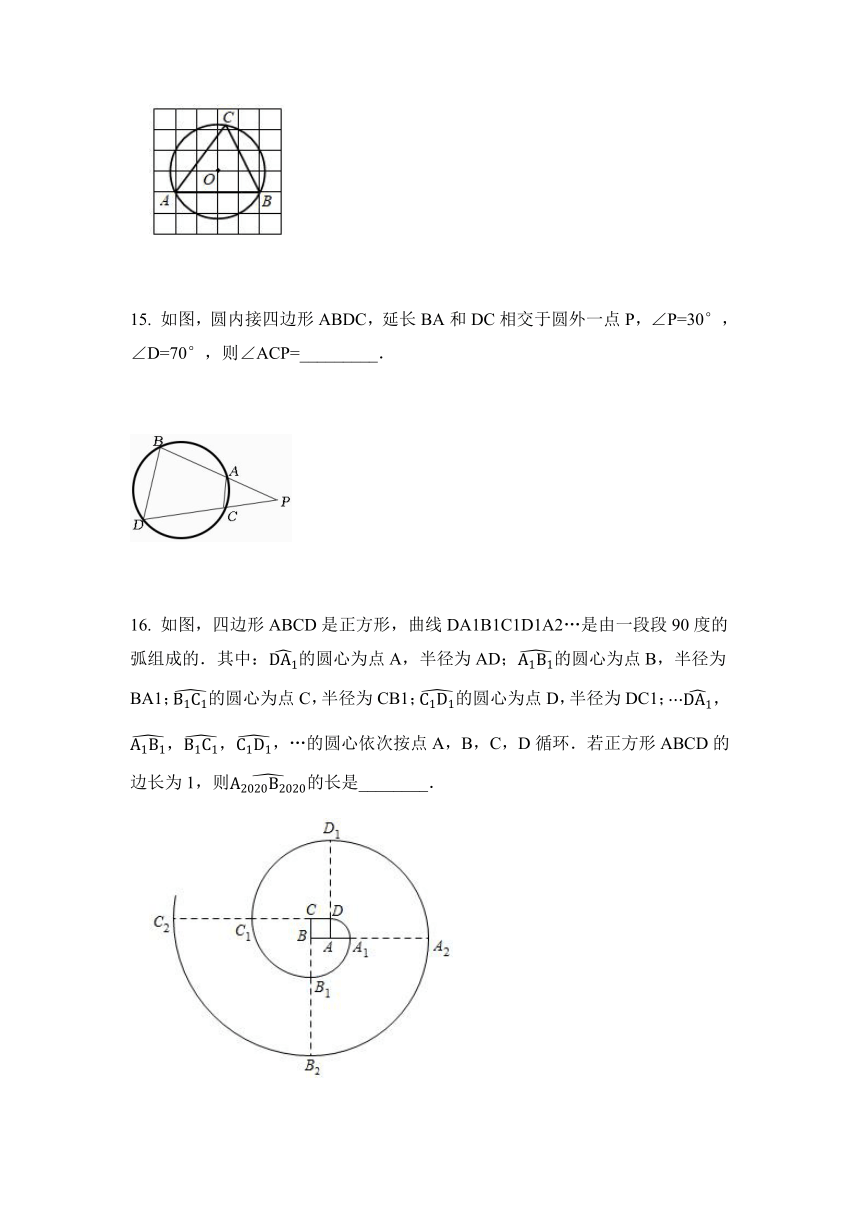
如图,在正方形网格中,每个小正方形的边长都是1,⊙O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是________. .
如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°, ∠D=70°,则∠ACP=_________.
如图,四边形ABCD是正方形,曲线DA1B1C1D1A2…是由一段段90度的弧组成的.其中:的圆心为点A,半径为AD;的圆心为点B,半径为BA1;的圆心为点C,半径为CB1;的圆心为点D,半径为DC1;,…的圆心依次按点A,B,C,D循环.若正方形ABCD的边长为1,则的长是________.
三.解答题(17题8分,18题10分,19题12分,20题16分)
17. ⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5cm,问:A、B、C三点与⊙O的位置关系各是怎样?
18.如图,以等边三角形ABC的BC边为直径画圆,交AC于点D,DF⊥AB于点F,连接OF,且AF=1.
(1)求证:DF是的切线;
(2)求线段OF的长度.
如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
如图1,O为半圆的圆心,C、D为半圆上的两点,且.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
答案
1-5 AACBB 6-10 CBABA
11. 36°,18°,144°
12. 130°
13. 3
14.
15. 80°
16. 4039π
17. 点A在圆内,点B在圆上,点C在圆外
18.(1)证明:连接OD,
∵△ABC是等边三角形,
∴∠C=∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠CDO=∠A=60°,
∴OD∥AB,
∵DF⊥AB,
∴∠FDO=∠AFD=90°,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:∵OD∥AB,OC=OB,
∴OD是△ABC的中位线,
∵∠AFD=90°,∠A=60°,
∴∠ADF=30°,
∵AF=1
∴CD=OD=AD=2AF=2,
由勾股定理得:DF2=3,
在Rt△ODF中,OF,
∴线段OF的长为.
19. 分析:(1)根据圆周角定理得到∠ACB=∠ACD=90°,根据直角三角形的性质得到
CF=EF=DF,求得∠AEO=∠FEC=∠FCE,根据等腰三角形的性质得到∠OCA=∠OAC,于是得到结论,
(2)根据三角形的内角和得到∠OAE=∠CDE=22.5°,根据等腰三角形的性质得到∠CAD=∠ADC=45°,于是得到结论.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
∵点F是ED的中点,
∴CF=EF=DF,
∴∠AEO=∠FEC=∠FCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OD⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠FCE=90°,即OC⊥FC,
∴CF与⊙O相切,
(2)解:∵OD⊥AB,AC⊥BD,
∴∠AOE=∠ACD=90°,
∵∠AEO=∠DEC,
∴∠OAE=∠CDE=22.5°,
∵AO=BO,
∴AD=BD,
∴∠ADO=∠BDO=22.5°,
∴∠ADB=45°,
∴∠CAD=∠ADC=45°,
∴AC=CD.
20.(1)证明:如图1中,连接BC.
∵,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴CD=ED.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴,
∴,
∴CF AF=OF AH.
②解:如图3中,连接OD交BC于G.设OG=x,则DG=2﹣x.
∵,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x,即OG,
∵OA=OB,
∴OG是△ABC的中位线,
∴OGAC,
∴AC.
一、选择题(每题3分)
1.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5 B.10 C.8 D.6
2.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )
A.1 B.2 C. D.
如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=60°,则∠B等于( )
A.30° B.35° C.40° D.50°
如图,BD是○O的直径,点A,C在上,,
AC交BD于点G.若∠COD=126°.则∠AGB的度数为( )
99° B.108°
110° D.117°
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
π B.2π C.3π D.4π
6. 如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.22 B.3 C.4 D.2
7.如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
如图,AB是⊙O的直径,CD为⊙O的弦,AB⊥CD于点E,若CD=6,AE=9,则阴影部分的面积为( )
A.6π B.12π﹣9 C.3π D.9
如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
如图,△ABC内接于⊙O,AD⊥BC, BE⊥AC,AD,BE相交于点M,若
AC=8,BM=4,则⊙O 的半径等于( )
A. B. C. D.6
二、填空题(每题4分)
11. 如图,为的直径,为弦,且弧BC=4弧AC,则______°,________°,________°.
12. 已知四边形内接于,如果,那么________.
13. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
如图,在正方形网格中,每个小正方形的边长都是1,⊙O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是________. .
如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°, ∠D=70°,则∠ACP=_________.
如图,四边形ABCD是正方形,曲线DA1B1C1D1A2…是由一段段90度的弧组成的.其中:的圆心为点A,半径为AD;的圆心为点B,半径为BA1;的圆心为点C,半径为CB1;的圆心为点D,半径为DC1;,…的圆心依次按点A,B,C,D循环.若正方形ABCD的边长为1,则的长是________.
三.解答题(17题8分,18题10分,19题12分,20题16分)
17. ⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5cm,问:A、B、C三点与⊙O的位置关系各是怎样?
18.如图,以等边三角形ABC的BC边为直径画圆,交AC于点D,DF⊥AB于点F,连接OF,且AF=1.
(1)求证:DF是的切线;
(2)求线段OF的长度.
如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
如图1,O为半圆的圆心,C、D为半圆上的两点,且.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
答案
1-5 AACBB 6-10 CBABA
11. 36°,18°,144°
12. 130°
13. 3
14.
15. 80°
16. 4039π
17. 点A在圆内,点B在圆上,点C在圆外
18.(1)证明:连接OD,
∵△ABC是等边三角形,
∴∠C=∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠CDO=∠A=60°,
∴OD∥AB,
∵DF⊥AB,
∴∠FDO=∠AFD=90°,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:∵OD∥AB,OC=OB,
∴OD是△ABC的中位线,
∵∠AFD=90°,∠A=60°,
∴∠ADF=30°,
∵AF=1
∴CD=OD=AD=2AF=2,
由勾股定理得:DF2=3,
在Rt△ODF中,OF,
∴线段OF的长为.
19. 分析:(1)根据圆周角定理得到∠ACB=∠ACD=90°,根据直角三角形的性质得到
CF=EF=DF,求得∠AEO=∠FEC=∠FCE,根据等腰三角形的性质得到∠OCA=∠OAC,于是得到结论,
(2)根据三角形的内角和得到∠OAE=∠CDE=22.5°,根据等腰三角形的性质得到∠CAD=∠ADC=45°,于是得到结论.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
∵点F是ED的中点,
∴CF=EF=DF,
∴∠AEO=∠FEC=∠FCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OD⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠FCE=90°,即OC⊥FC,
∴CF与⊙O相切,
(2)解:∵OD⊥AB,AC⊥BD,
∴∠AOE=∠ACD=90°,
∵∠AEO=∠DEC,
∴∠OAE=∠CDE=22.5°,
∵AO=BO,
∴AD=BD,
∴∠ADO=∠BDO=22.5°,
∴∠ADB=45°,
∴∠CAD=∠ADC=45°,
∴AC=CD.
20.(1)证明:如图1中,连接BC.
∵,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴CD=ED.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴,
∴,
∴CF AF=OF AH.
②解:如图3中,连接OD交BC于G.设OG=x,则DG=2﹣x.
∵,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x,即OG,
∵OA=OB,
∴OG是△ABC的中位线,
∴OGAC,
∴AC.
