2022年新教材高中数学第五章统计与概率1.4用样本估计总体课件新人教B版必修第二册 课件(共17张PPT)
文档属性
| 名称 | 2022年新教材高中数学第五章统计与概率1.4用样本估计总体课件新人教B版必修第二册 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:34:50 | ||
图片预览






文档简介
(共17张PPT)
5.1.4 用样本估计总体
1.理解用样本的数字特征估计总体的数字特征的方法.
2.能用样本的分布估计总体的分布.
3.会应用相关知识解决实际统计问题.
1 |用样本的数字特征估计总体的数字特征
利用随机抽样得到样本,从样本数据得到的平均数和标准差(通常也称为样
本均值和样本标准差)并不是总体真正的平均数和标准差,而只是对总体的一个
① 估计 ,但这种估计是合理的,特别是当样本容量很大时,它们确实反映了总
体的信息.
2 |用样本的分布估计总体的分布
当样本容量不断增大时,样本中落在每个区间内的样本数的频率会越来越稳
定于总体在相应区间内取值的概率.也就是说,一般地,样本容量② 越大 ,用样
本的频率分布去估计总体的分布就越准确.
1.在容许一定误差存在的前提下,可以用样本的数字特征去估计总体的数字特征,
这样就能节省人力和物力等. ( √ )
判断正误,正确的画“ √” ,错误的画“ ” 。
2.有时候总体的数字特征不可能获得,此时只能用样本的数字特征去估计总体的
数字特征.( √ )
3.一般来说,在估计总体的数字特征时,只需直接算出样本对应的数字特征即可.
( √ )
4.同数字特征的估计一样,分布的估计一般也有误差. ( √ )
5.在记录两个人射击环数的两组数据中,方差大的表示射击水平高. ( )
1 |用样本的数字特征估计总体的数字特征
1.一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够
反映总体的特征.在允许一定误差存在的前提下,可以用样本的数字特征去估计
总体的数字特征.
2.用样本估计总体是研究统计问题的一个基本思想方法,即用样本平均数估计总
体平均数,用样本方差估计总体方差(方差和标准差是描述一个样本或总体的波
动大小的特征数,方差或标准差越小,表示这个样本或总体的波动越小,即越稳定).
一般地,样本容量越大,这种估计就越准确.
3.利用样本估计总体的目的是通过对样本平均数和方差的比较,能对总体进行全
面的分析、比较,进而提出合理的建议和指导意见,对实际应用问题做出正确的
反馈.
1.平均数、中位数、众数与频率分布直方图的关系:
(1)众数在样本数据的频率分布直方图中,就是最高的小长方形中某个(些)点的横
坐标.
(2)由于在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中
位数,因此在频率分布直方图中,中位数左侧和右侧的小长方形的面积和应该相
等,据此可以估计中位数的值.
(3)平均数是频率分布直方图的“重心”,是直方图的平衡点.用频率分布直方图
估计平均数时,平均数的估计值等于频率分布直方图中每个小长方形的面积与小
长方形底边中点的横坐标(组中值)之积的和.
2.利用直方图求得的众数、中位数和平均数均为近似值,往往与由实际数据得出
的不一致,但它们能粗略估计众数、中位数和平均数.
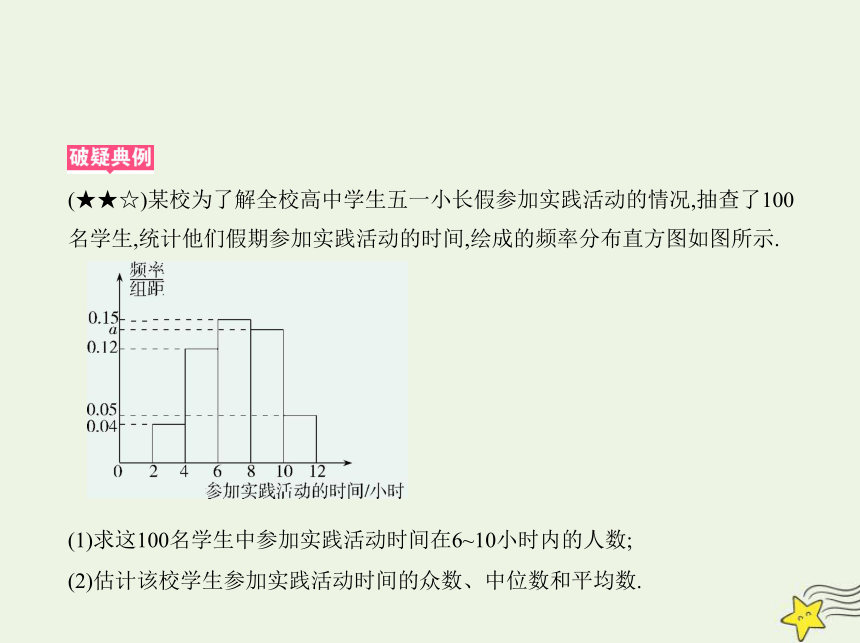
(★★☆)某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100
名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计该校学生参加实践活动时间的众数、中位数和平均数.
思路点拨:
(1)先求数据不在6~10小时内的频率,进而求出数据在6~10小时内的频率,由频数=
样本容量×频率计算.(2)在频率分布直方图中,众数是最高矩形底边中点的横坐
标;中位数左边和右边的小矩形的面积和相等;平均数等于组中值与对应频率之
积的和.
解析 (1)100×[1-(0.04+0.12+0.05)×2]=58,
即这100名学生中参加实践活动时间在6~10小时内的人数为58.
(2)由频率分布直方图可以看出最高矩形底边中点的横坐标为7,故该校学生参加
实践活动时间的众数的估计值为7小时;
(0.04+0.12)×2=0.32,(0.04+0.12+0.15)×2=0.62,
∵0.32<0.5<0.62,
∴中位数t满足6由0.32+(t-6)×0.15=0.5,得t=7.2,
即该校学生参加实践活动时间的中位数的估计值为7.2小时;
由(0.04+0.12+0.15+a+0.05)×2=1,
解得a=0.14,
该校学生参加实践活动时间的平均数的估计值为0.04×2×3+0.12×2×5+0.15×2×7
+0.14×2×9+0.05×2×11=7.16(小时).
2|用样本的分布估计总体的分布
为了了解中学生的身高情况,对某校同龄的50名男同学的身高进行了测量(单位:
cm),结果如下:
175 168 170 176 167 181 162 173 171 177
171 171 174 173 174 175 177 166 163 160
166 166 163 169 174 165 175 165 170 158
174 172 166 172 167 172 175 161 173 167
170 172 165 157 172 173 166 177 169 181
问题
1.以上数据可采用什么方法进行统计
提示:列样本的频率分布表,画频率分布直方图.
2.以上数据的极差是多少 如果要对数据分组,怎么分组较合理
提示:极差=181-157=24;分成七组或八组较合理,分组如表:
分组 频数 频率
156.5~160.5 3 0.06
160.5~164.5 4 0.08
164.5~168.5 12 0.24
168.5~172.5 13 0.26
172.5~176.5 13 0.26
176.5~180.5 3 0.06
180.5~184.5 2 0.04
合计 50 1.00
3.如何在已有的频率分布直方图上画出频率分布折线图
提示:在频率分布直方图上顺次连接各个小矩形上面一边的中点得频率分布折线
图.
4.根据已有的样本数据及统计分析估计该校同龄男同学的身高状况.
提示:估计该校同龄男同学的身高多数集中在164 cm到177 cm之间.
1.如果样本容量恰当,抽样方法又合理,在允许有一定误差的前提下,可以用样本
的分布去估计总体的分布.
频率分布是指一个样本数据在各个小范围内所占比例的大小.一般利用频率分布
表和频率分布直方图来直观体现.
2.如何用样本分布估计总体分布
一般是利用样本在某一范围内的频率近似地估计总体在该范围内的频率.所以,
首先样本抽取要合理科学,其次要正确绘制频率分布表(或直方图),或者要准确找
出题目所给频率分布表(或直方图)中的相关信息,最后由样本分布估计出总体分
布情况.
(★★☆)为了了解学生的身体发育情况,某校对年满16周岁的60名男生的身高进
行测量,其结果如下:
身高/m 1.57 1.59 1.60 1.62 1.63 1.64 1.65 1.66 1.68
人数 2 1 3 2 3 4 2 7 6
身高/m 1.69 1.70 1.71 1.72 1.73 1.74 1.75 1.76 1.77
人数 8 7 4 3 2 1 2 1 2
(1)根据上表,估计在这所学校年满16周岁的男生中,身高不低于1.65 m且不高于1.
71 m的男生所占的比例,及身高不低于1.63 m的男生所占的比例;
(2)将测量数据分为5组,画出样本频率分布直方图和频率分布折线图;
(3)根据(2)中的统计图说明该校年满16周岁的男生的身高在哪一范围内的人数所
占的比例最大.如果年满16周岁的男生有1 200人,那么估计在这个身高范围内的
男生有多少人.
思路点拨:
(1)由表中数据直接计算所求问题;(2)根据极差确定组距,然后分组并计算每组的
频数和频率,画出频率分布直方图和频率分布折线图;(3)根据统计图可知身高在
[1.69,1.73)范围内的男生所占比例最大,用此范围的频率乘总数即可求得结果.
解析 (1)由题中表格可知,身高不低于1.65 m且不高于1.71 m的人数为2+7+6+8+
7+4=34,在样本中所占比例为 ×100%≈56.7%;身高不低于1.63 m的人数为60-2-
1-3-2=52,在样本中所占比例为 ×100%≈86.7%.
因此可估计这所学校年满16周岁的男生中,身高不低于1.65 m且不高于1.71 m的
男生所占的比例为56.7%,身高不低于1.63 m的男生所占的比例为86.7%.
(2)数据的极差为1.77-1.57=0.20,由此确定组距为0.04,频率分布表如下:
分组 频数 频率
[1.57,1.61) 6 0.1
[1.61,1.65) 9 0.15
[1.65,1.69) 15 0.25
[1.69,1.73) 22 0.366 7
[1.73,1.77] 8 0.133 3
合计 60 1
频率分布直方图与频率分布折线图如下:
(3)根据频率分布直方图可知,身高在[1.69,1.73)范围内的男生所占的比例最大,由
全校年满16周岁的男生人数为1 200,可估计在该身高范围内的男生有1 200×0.36
6 7≈440(人).
5.1.4 用样本估计总体
1.理解用样本的数字特征估计总体的数字特征的方法.
2.能用样本的分布估计总体的分布.
3.会应用相关知识解决实际统计问题.
1 |用样本的数字特征估计总体的数字特征
利用随机抽样得到样本,从样本数据得到的平均数和标准差(通常也称为样
本均值和样本标准差)并不是总体真正的平均数和标准差,而只是对总体的一个
① 估计 ,但这种估计是合理的,特别是当样本容量很大时,它们确实反映了总
体的信息.
2 |用样本的分布估计总体的分布
当样本容量不断增大时,样本中落在每个区间内的样本数的频率会越来越稳
定于总体在相应区间内取值的概率.也就是说,一般地,样本容量② 越大 ,用样
本的频率分布去估计总体的分布就越准确.
1.在容许一定误差存在的前提下,可以用样本的数字特征去估计总体的数字特征,
这样就能节省人力和物力等. ( √ )
判断正误,正确的画“ √” ,错误的画“ ” 。
2.有时候总体的数字特征不可能获得,此时只能用样本的数字特征去估计总体的
数字特征.( √ )
3.一般来说,在估计总体的数字特征时,只需直接算出样本对应的数字特征即可.
( √ )
4.同数字特征的估计一样,分布的估计一般也有误差. ( √ )
5.在记录两个人射击环数的两组数据中,方差大的表示射击水平高. ( )
1 |用样本的数字特征估计总体的数字特征
1.一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够
反映总体的特征.在允许一定误差存在的前提下,可以用样本的数字特征去估计
总体的数字特征.
2.用样本估计总体是研究统计问题的一个基本思想方法,即用样本平均数估计总
体平均数,用样本方差估计总体方差(方差和标准差是描述一个样本或总体的波
动大小的特征数,方差或标准差越小,表示这个样本或总体的波动越小,即越稳定).
一般地,样本容量越大,这种估计就越准确.
3.利用样本估计总体的目的是通过对样本平均数和方差的比较,能对总体进行全
面的分析、比较,进而提出合理的建议和指导意见,对实际应用问题做出正确的
反馈.
1.平均数、中位数、众数与频率分布直方图的关系:
(1)众数在样本数据的频率分布直方图中,就是最高的小长方形中某个(些)点的横
坐标.
(2)由于在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中
位数,因此在频率分布直方图中,中位数左侧和右侧的小长方形的面积和应该相
等,据此可以估计中位数的值.
(3)平均数是频率分布直方图的“重心”,是直方图的平衡点.用频率分布直方图
估计平均数时,平均数的估计值等于频率分布直方图中每个小长方形的面积与小
长方形底边中点的横坐标(组中值)之积的和.
2.利用直方图求得的众数、中位数和平均数均为近似值,往往与由实际数据得出
的不一致,但它们能粗略估计众数、中位数和平均数.
(★★☆)某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100
名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计该校学生参加实践活动时间的众数、中位数和平均数.
思路点拨:
(1)先求数据不在6~10小时内的频率,进而求出数据在6~10小时内的频率,由频数=
样本容量×频率计算.(2)在频率分布直方图中,众数是最高矩形底边中点的横坐
标;中位数左边和右边的小矩形的面积和相等;平均数等于组中值与对应频率之
积的和.
解析 (1)100×[1-(0.04+0.12+0.05)×2]=58,
即这100名学生中参加实践活动时间在6~10小时内的人数为58.
(2)由频率分布直方图可以看出最高矩形底边中点的横坐标为7,故该校学生参加
实践活动时间的众数的估计值为7小时;
(0.04+0.12)×2=0.32,(0.04+0.12+0.15)×2=0.62,
∵0.32<0.5<0.62,
∴中位数t满足6
即该校学生参加实践活动时间的中位数的估计值为7.2小时;
由(0.04+0.12+0.15+a+0.05)×2=1,
解得a=0.14,
该校学生参加实践活动时间的平均数的估计值为0.04×2×3+0.12×2×5+0.15×2×7
+0.14×2×9+0.05×2×11=7.16(小时).
2|用样本的分布估计总体的分布
为了了解中学生的身高情况,对某校同龄的50名男同学的身高进行了测量(单位:
cm),结果如下:
175 168 170 176 167 181 162 173 171 177
171 171 174 173 174 175 177 166 163 160
166 166 163 169 174 165 175 165 170 158
174 172 166 172 167 172 175 161 173 167
170 172 165 157 172 173 166 177 169 181
问题
1.以上数据可采用什么方法进行统计
提示:列样本的频率分布表,画频率分布直方图.
2.以上数据的极差是多少 如果要对数据分组,怎么分组较合理
提示:极差=181-157=24;分成七组或八组较合理,分组如表:
分组 频数 频率
156.5~160.5 3 0.06
160.5~164.5 4 0.08
164.5~168.5 12 0.24
168.5~172.5 13 0.26
172.5~176.5 13 0.26
176.5~180.5 3 0.06
180.5~184.5 2 0.04
合计 50 1.00
3.如何在已有的频率分布直方图上画出频率分布折线图
提示:在频率分布直方图上顺次连接各个小矩形上面一边的中点得频率分布折线
图.
4.根据已有的样本数据及统计分析估计该校同龄男同学的身高状况.
提示:估计该校同龄男同学的身高多数集中在164 cm到177 cm之间.
1.如果样本容量恰当,抽样方法又合理,在允许有一定误差的前提下,可以用样本
的分布去估计总体的分布.
频率分布是指一个样本数据在各个小范围内所占比例的大小.一般利用频率分布
表和频率分布直方图来直观体现.
2.如何用样本分布估计总体分布
一般是利用样本在某一范围内的频率近似地估计总体在该范围内的频率.所以,
首先样本抽取要合理科学,其次要正确绘制频率分布表(或直方图),或者要准确找
出题目所给频率分布表(或直方图)中的相关信息,最后由样本分布估计出总体分
布情况.
(★★☆)为了了解学生的身体发育情况,某校对年满16周岁的60名男生的身高进
行测量,其结果如下:
身高/m 1.57 1.59 1.60 1.62 1.63 1.64 1.65 1.66 1.68
人数 2 1 3 2 3 4 2 7 6
身高/m 1.69 1.70 1.71 1.72 1.73 1.74 1.75 1.76 1.77
人数 8 7 4 3 2 1 2 1 2
(1)根据上表,估计在这所学校年满16周岁的男生中,身高不低于1.65 m且不高于1.
71 m的男生所占的比例,及身高不低于1.63 m的男生所占的比例;
(2)将测量数据分为5组,画出样本频率分布直方图和频率分布折线图;
(3)根据(2)中的统计图说明该校年满16周岁的男生的身高在哪一范围内的人数所
占的比例最大.如果年满16周岁的男生有1 200人,那么估计在这个身高范围内的
男生有多少人.
思路点拨:
(1)由表中数据直接计算所求问题;(2)根据极差确定组距,然后分组并计算每组的
频数和频率,画出频率分布直方图和频率分布折线图;(3)根据统计图可知身高在
[1.69,1.73)范围内的男生所占比例最大,用此范围的频率乘总数即可求得结果.
解析 (1)由题中表格可知,身高不低于1.65 m且不高于1.71 m的人数为2+7+6+8+
7+4=34,在样本中所占比例为 ×100%≈56.7%;身高不低于1.63 m的人数为60-2-
1-3-2=52,在样本中所占比例为 ×100%≈86.7%.
因此可估计这所学校年满16周岁的男生中,身高不低于1.65 m且不高于1.71 m的
男生所占的比例为56.7%,身高不低于1.63 m的男生所占的比例为86.7%.
(2)数据的极差为1.77-1.57=0.20,由此确定组距为0.04,频率分布表如下:
分组 频数 频率
[1.57,1.61) 6 0.1
[1.61,1.65) 9 0.15
[1.65,1.69) 15 0.25
[1.69,1.73) 22 0.366 7
[1.73,1.77] 8 0.133 3
合计 60 1
频率分布直方图与频率分布折线图如下:
(3)根据频率分布直方图可知,身高在[1.69,1.73)范围内的男生所占的比例最大,由
全校年满16周岁的男生人数为1 200,可估计在该身高范围内的男生有1 200×0.36
6 7≈440(人).
