2022年新教材高中数学第四章指数函数对数函数与幂函数6_7数学建模活动生长规律的描述课件新人教B版必修第二册(共18张PPT)
文档属性
| 名称 | 2022年新教材高中数学第四章指数函数对数函数与幂函数6_7数学建模活动生长规律的描述课件新人教B版必修第二册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:39:07 | ||
图片预览






文档简介
(共18张PPT)
4.6 函数的应用(二)
4.7 数学建模活动:生长规律的描述
1.理解函数模型是描述客观世界中变量关系和规律的重要的数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律.
3.收集一些现实生活、生产实际或者经济领域中的数学模型,体会人们是如何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
1 |常见函数模型
一次函数模型 y=kx+b(k,b为常数,k≠0)
二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
指数型函数 模型 y=bax+c(a,b,c为常数,b≠0,a>0
且a≠1)
对数型函数 模型 y=mlogax+n(m,a,n为常数,m≠
0,a>0且a≠1)
幂函数型模型 y=axn+b(a,b,n为常数,a≠0)
2 |建立函数模型解决问题的基本过程
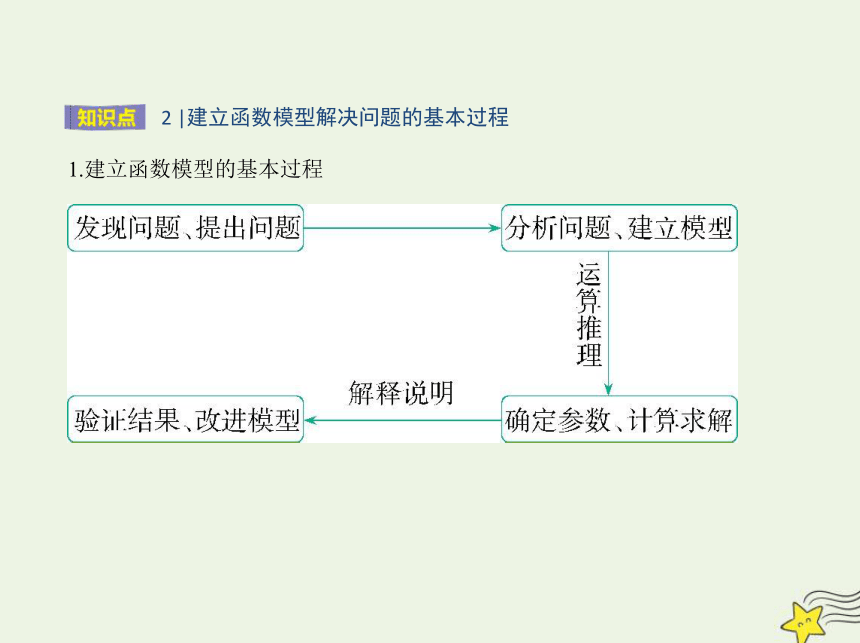
1.建立函数模型的基本过程
2.建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学
知识建立相应的函数模型;
(3)求模——推理求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
判断正误,正确的画“ √” ,错误的画“ ” 。
1.解决某一实际问题的函数模型是唯一的.( )
2.对于一个实际问题,收集到的数据越多,建立的函数模型的模拟效果越好. ( √ )
3.根据收集到的数据作出散点图,结合已知的函数选择适当的函数模型,这样得到
的函数模型的模拟效果较好. ( √ )
4.函数模型中,要求定义域只需使函数式有意义. ( )
提示:在函数模型中,除了要使函数式有意义,还要使实际问题有意义.
5.用函数模型预测的结果和实际结果必须相等,否则函数模型就没有存在的意义
了. ( )
1 |构建函数模型解决实际问题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销量,增
加盈利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每
降价1元,商场平均每天可多售出2件.于是商场经理决定每件衬衫降价15元.
问题
1.请问经理的决定正确吗
提示:判断是否正确,这需要把实际问题转化为数学问题,用函数模型来解决.
2.解决函数应用问题的基本步骤是什么
提示:用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:①审题;
②建模;③求模;④还原.
1.构建函数模型时的四个关键:
(1)求什么,就是弄清楚要解决什么问题或完成什么任务.
(2)设什么,就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自
变量.
(3)列什么,就是把问题的已知条件用所设变量表示出来,可以是方程、函数、不
等式等.
(4)限制什么,主要是指自变量应满足的限制条件,在实际问题中,除了要使函数式
有意义外,还要考虑变量的实际含义,如生产的零件不能是半个等.
2.建立函数模型时,求解函数解析式的方法:
(1)待定系数法.已知条件中给出了含参数的函数解析式或根据已知条件可确定
函数模型时,应用待定系数法求出函数解析式中的相关参数(未知系数)的值,就可
以确定函数的解析式.
(2)归纳法.先让自变量x取一些特殊值,计算出相对应的函数值,从中发现规律,再
推广到一般情形,从而得到函数的解析式.
(3)方程法.用x表示自变量或其他相关的量.根据问题的实际意义,运用已掌握的数
学、物理等方面的知识,列出函数的解析式,此种方法形式上和列方程解应用题
相仿,故称为方程法.
(★★☆)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:
“活水围网”养鱼时,某种鱼在一定条件下,每尾鱼的平均生长速度v(单位:千克/
年)是关于养殖密度x(单位:尾/立方米)的函数.当养殖密度x不超过4尾/立方米时,v
为2千克/年;当4时,因缺氧等原因,v为0千克/年.
(1)当0(2)当养殖密度x为多大时,该种鱼的年生长量f(x)(单位:千克/立方米)可以达到最
大 最大为多少 (年生长量=每尾鱼的平均生长速度×养殖密度)
解析 (1)由题意得,当0当4由已知得 解得 所以v=- x+ .
故v=
(2)依题意及(1)可得f(x)=
当0故f(x)max=f(4)=4×2=8;
当4所以f(x)max=f(10)= =12.5.
因为8<12.5,所以当0所以当养殖密度x为10尾/立方米时,该种鱼的年生长量f(x)可以达到最大,最大为1
2.5千克/立方米.
2|建立拟合函数模型解决实际问题
李明家种植蔬菜,他研究了黄瓜的种植成本与上市时间的关系.黄瓜从1月1日开
始上市,通过市场调查,得到该黄瓜的种植成本Q(单位:元/10 kg)与上市时间t(单
位:10天)的数据如下表:
时间t(10天) 5 6 11 25
种植成本Q(元/10
kg) 15 14.03 10.8 15
问题
1.根据表中数据,如何选取一个合适的函数模型描述该蔬菜种植成本Q(单位:元/
10 kg)与上市时间t(单位:10天)的变化关系
提示:画散点图,根据图形确定拟合函数.
2.根据散点图如何确定函数模型
提示:根据散点分布特征对比基本函数图像确定模型类型.
函数拟合与预测的一般步骤:
(1)根据原始数据、表格,绘出散点图;
(2)通过散点图,画出拟合直线或拟合曲线;
(3)求出拟合直线或拟合曲线的函数关系式;
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依
据.
拔高问题
3.用得到的函数进行拟合,是否一定符合实际问题
提示:不一定.用得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要
对所得函数模型进行检验,切忌盲目下结论.
(★★☆)某人对西红柿市场做了一次调查,通过调查,得到西红柿种植成本Q(单
位:元/102 kg)与上市时间t(单位:天)的数据如下表:
上市时间t(天) 50 110 250
种植成本Q(元/102 kg) 150 108 150
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间
t的变化关系.
Q=at+b,Q=at2+bt+c,
Q=a·bt,Q=a·logbt.
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
思路点拨:
作图筛选出较好的方案,再通过计算进行确认,从而选出合适的函数模型.
解析 (1)作出散点图,如图,根据散点图,应选取二次函数Q=at2+bt+c进行描述.
由题意知
解得a= ,b=- ,c= .
∴Q= t2- t+ .
(2)由(1)知,Q= (t-150)2+100,
∴当t=150时,西红柿的种植成本最低,为100元/102 kg.
4.6 函数的应用(二)
4.7 数学建模活动:生长规律的描述
1.理解函数模型是描述客观世界中变量关系和规律的重要的数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律.
3.收集一些现实生活、生产实际或者经济领域中的数学模型,体会人们是如何借助函数刻画实际问题的,感悟数学模型中参数的现实意义.
1 |常见函数模型
一次函数模型 y=kx+b(k,b为常数,k≠0)
二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
指数型函数 模型 y=bax+c(a,b,c为常数,b≠0,a>0
且a≠1)
对数型函数 模型 y=mlogax+n(m,a,n为常数,m≠
0,a>0且a≠1)
幂函数型模型 y=axn+b(a,b,n为常数,a≠0)
2 |建立函数模型解决问题的基本过程
1.建立函数模型的基本过程
2.建立函数模型解决实际问题的步骤
(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择函数模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学
知识建立相应的函数模型;
(3)求模——推理求解函数模型;
(4)还原——用得到的函数模型描述实际问题的变化规律.
判断正误,正确的画“ √” ,错误的画“ ” 。
1.解决某一实际问题的函数模型是唯一的.( )
2.对于一个实际问题,收集到的数据越多,建立的函数模型的模拟效果越好. ( √ )
3.根据收集到的数据作出散点图,结合已知的函数选择适当的函数模型,这样得到
的函数模型的模拟效果较好. ( √ )
4.函数模型中,要求定义域只需使函数式有意义. ( )
提示:在函数模型中,除了要使函数式有意义,还要使实际问题有意义.
5.用函数模型预测的结果和实际结果必须相等,否则函数模型就没有存在的意义
了. ( )
1 |构建函数模型解决实际问题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销量,增
加盈利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每
降价1元,商场平均每天可多售出2件.于是商场经理决定每件衬衫降价15元.
问题
1.请问经理的决定正确吗
提示:判断是否正确,这需要把实际问题转化为数学问题,用函数模型来解决.
2.解决函数应用问题的基本步骤是什么
提示:用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:①审题;
②建模;③求模;④还原.
1.构建函数模型时的四个关键:
(1)求什么,就是弄清楚要解决什么问题或完成什么任务.
(2)设什么,就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自
变量.
(3)列什么,就是把问题的已知条件用所设变量表示出来,可以是方程、函数、不
等式等.
(4)限制什么,主要是指自变量应满足的限制条件,在实际问题中,除了要使函数式
有意义外,还要考虑变量的实际含义,如生产的零件不能是半个等.
2.建立函数模型时,求解函数解析式的方法:
(1)待定系数法.已知条件中给出了含参数的函数解析式或根据已知条件可确定
函数模型时,应用待定系数法求出函数解析式中的相关参数(未知系数)的值,就可
以确定函数的解析式.
(2)归纳法.先让自变量x取一些特殊值,计算出相对应的函数值,从中发现规律,再
推广到一般情形,从而得到函数的解析式.
(3)方程法.用x表示自变量或其他相关的量.根据问题的实际意义,运用已掌握的数
学、物理等方面的知识,列出函数的解析式,此种方法形式上和列方程解应用题
相仿,故称为方程法.
(★★☆)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:
“活水围网”养鱼时,某种鱼在一定条件下,每尾鱼的平均生长速度v(单位:千克/
年)是关于养殖密度x(单位:尾/立方米)的函数.当养殖密度x不超过4尾/立方米时,v
为2千克/年;当4
(1)当0
大 最大为多少 (年生长量=每尾鱼的平均生长速度×养殖密度)
解析 (1)由题意得,当0
故v=
(2)依题意及(1)可得f(x)=
当0
当4
因为8<12.5,所以当0
2.5千克/立方米.
2|建立拟合函数模型解决实际问题
李明家种植蔬菜,他研究了黄瓜的种植成本与上市时间的关系.黄瓜从1月1日开
始上市,通过市场调查,得到该黄瓜的种植成本Q(单位:元/10 kg)与上市时间t(单
位:10天)的数据如下表:
时间t(10天) 5 6 11 25
种植成本Q(元/10
kg) 15 14.03 10.8 15
问题
1.根据表中数据,如何选取一个合适的函数模型描述该蔬菜种植成本Q(单位:元/
10 kg)与上市时间t(单位:10天)的变化关系
提示:画散点图,根据图形确定拟合函数.
2.根据散点图如何确定函数模型
提示:根据散点分布特征对比基本函数图像确定模型类型.
函数拟合与预测的一般步骤:
(1)根据原始数据、表格,绘出散点图;
(2)通过散点图,画出拟合直线或拟合曲线;
(3)求出拟合直线或拟合曲线的函数关系式;
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依
据.
拔高问题
3.用得到的函数进行拟合,是否一定符合实际问题
提示:不一定.用得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要
对所得函数模型进行检验,切忌盲目下结论.
(★★☆)某人对西红柿市场做了一次调查,通过调查,得到西红柿种植成本Q(单
位:元/102 kg)与上市时间t(单位:天)的数据如下表:
上市时间t(天) 50 110 250
种植成本Q(元/102 kg) 150 108 150
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间
t的变化关系.
Q=at+b,Q=at2+bt+c,
Q=a·bt,Q=a·logbt.
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
思路点拨:
作图筛选出较好的方案,再通过计算进行确认,从而选出合适的函数模型.
解析 (1)作出散点图,如图,根据散点图,应选取二次函数Q=at2+bt+c进行描述.
由题意知
解得a= ,b=- ,c= .
∴Q= t2- t+ .
(2)由(1)知,Q= (t-150)2+100,
∴当t=150时,西红柿的种植成本最低,为100元/102 kg.
