2022年新教材高中数学第四章指数函数对数函数与幂函数4幂函数课件新人教B版必修第二册(共16张PPT)
文档属性
| 名称 | 2022年新教材高中数学第四章指数函数对数函数与幂函数4幂函数课件新人教B版必修第二册(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:42:38 | ||
图片预览






文档简介
(共16张PPT)
4.4 幂函数
1.了解幂函数的概念、图像及性质,会求幂函数的解析式.
2.通过具体实例,结合y=x,y= ,y=x2,y= ,y=x3的图像,理解它们的变化规律.
3.能利用幂函数的单调性比较大小.
1 |幂函数的概念
一般地,函数① y=xα 称为幂函数,其中α是常数.
2 |五个幂函数的图像与性质
幂函数 y=x y=x2 y=x3 y= y=x-1
图像
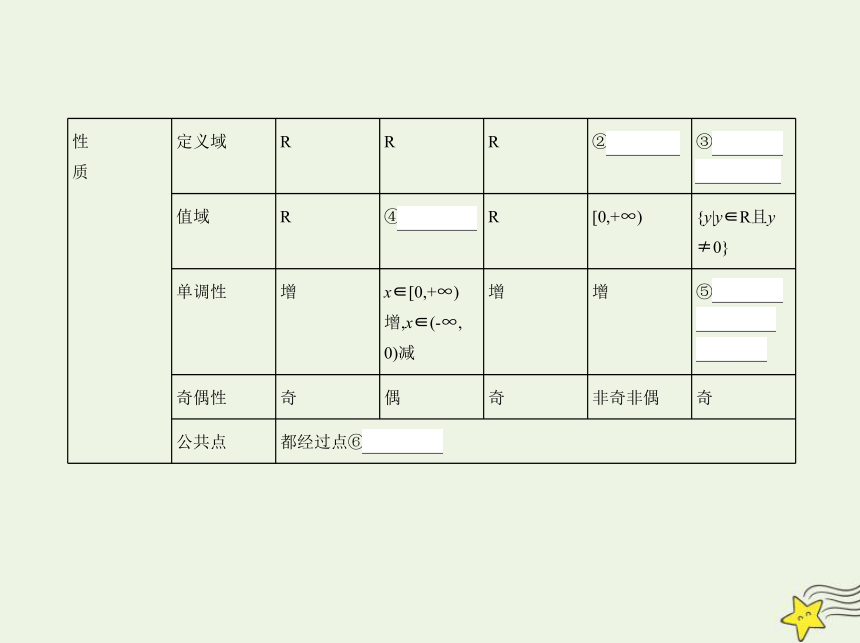
性 质 定义域 R R R ② [0,+∞) ③ (-∞,0)
∪(0,+∞)
值域 R ④ [0,+∞)
R [0,+∞) {y|y∈R且y
≠0}
单调性 增 x∈[0,+∞)
增,x∈(-∞,
0)减 增 增 ⑤ x∈(0,+
∞)减,x∈(-
∞,0)减
奇偶性 奇 偶 奇 非奇非偶 奇
公共点 都经过点⑥ (1,1)
判断正误,正确的画“ √” ,错误的画“ ” 。
1.幂函数的图像都过点(0,0),(1,1). ( )
2.幂函数的图像一定不能出现在第四象限,但可能出现在第二象限. ( √ )
3.幂函数在(0,+∞)内不是增函数就是减函数. ( )
4.当α=0时,幂函数y=xα的图像是一条直线.( )
5.指数函数y=ax的定义域为R,与底数a无关,幂函数y=xα的定义域为R,与指数也无
关. ( )
1 |如何把握幂函数的图像
前面我们已熟悉下面几个函数:y= =x-1,y=x,y=x2,y= = .
问题
1.它们有什么结构特点
提示:可从幂的底数与幂指数考虑.
2.在同一坐标系内作出它们的图像并试着总结它们可能具有的性质.
提示:从图像的位置,单调性,对称性,过定点等方面考虑.
解决幂函数图像问题应把握的两个原则:
(1)根据各幂函数在第一象限内的图像确定相应幂指数的大小关系.依据图像高
低判断幂指数大小,相关结论如下:
①在x∈(0,1)上,指数越大,幂函数图像越靠近x轴(简记为指大图低);
②在x∈(1,+∞)上,指数越大,幂函数图像越远离x轴(简记为指大图高).
(2)利用定义域及奇偶性确定函数在其他象限的图像.
(★★☆)若点( ,2)在幂函数f(x)的图像上,点 在幂函数g(x)的图像上,
问当x为何值时,有①f(x)>g(x) ②f(x)=g(x) ③f(x)思路点拨:
先由点在幂函数的图像上确定幂函数的解析式,再由解析式得到大致图像,利用
图像解决问题.
解析 设f(x)=xα(α为常数),因为点( ,2)在幂函数f(x)的图像上,所以将( ,2)代入
f(x)=xα中,得2=( )α,解得α=2,则f(x)=x2.同理,可求得g(x)=x-2.
在同一平面直角坐标系中作出幂函数f(x)=x2和g(x)=x-2的图像(如图所示),
观察图像可得:
①当x>1或x<-1时, f(x)>g(x).②当x=1或x=-1时, f(x)=g(x).③当-12|如何运用幂函数性质解决相关问题
已知幂函数f(x)= ,其中{m|-2函数;(2) x∈R,都有f(-x)+f(x)=0.
问题
1.同时满足(1)(2)的幂函数f(x)是否存在
提示:存在.因为{m|-2由f(x)是(0,+∞)上的增函数得-2m2-m+3>0,解得- 又 x∈R,都有f(-x)+f(x)=0,即f(-x)=-f(x),所以f(x)是奇函数,即-2m2-m+3是奇数.③
由①②③得m=0.因此存在同时满足(1)(2)的幂函数f(x).
2.若存在,如何求出f(x)的解析式,以及x∈[0,3]时f(x)的值域
提示:由问题1知m=0,此时f(x)=x3,且在区间[0,3]上是增函数,所以x∈[0,3]时,函数
f(x)的值域为[0,27].
幂函数的性质与参数α可以互相确定:
(1)幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确
定幂函数的定义域、值域、单调性、奇偶性.
(2)由幂函数的性质可限制α的取值:
①利用幂函数的单调性求出α的取值范围;
②由奇偶性结合其他限制条件确定α的值.
1.(★★☆)已知幂函数y=x3m-9(m∈N*)的图像关于y轴对称,且y=x3m-9(m∈N*)在(0,+
∞)上单调递减,求满足(a+1 < 的实数a的取值范围.
思路点拨:
由函数的性质确定参数m的值,再由函数的单调性解不等式.
解析 因为函数y=x3m-9在(0,+∞)上单调递减,所以3m-9<0,解得m<3.又m∈N*,所以
m=1,2.
因为幂函数y=x3m-9的图像关于y轴对称,所以3m-9为偶数,故m=1,则原不等式可化
为(a+1 <(3-2a .
由y= 在(-∞,0),(0,+∞)上单调递减得,
a+1>3-2a>0或3-2a是 a a<-1或 2.(★★☆)比较下列各组数中两个数的大小:
(1) 与 ;
(2) 与 ;
(3)0.2 与6.2 ;
(4)0.20.6与0.30.4.
思路点拨:
可以借助幂函数的单调性或中间量进行比较.
解析 (1)∵y= 是[0,+∞)上的增函数,且 > ,
∴ > .
(2)∵y=x-1是(-∞,0)上的减函数,且- <- ,∴ > .
(3)0.2 = = ,6.2 =2. .
∵y= 是[0,+∞)上的增函数,且2<2.5,
∴ <2. ,即0.2 <6.2 .
(4)由幂函数的单调性,知0.20.6<0.30.6,又y=0.3x是减函数,
∴0.30.4>0.30.6,从而0.20.6<0.30.4.
方法总结:
比较幂值的大小,关键在于构造适当的函数:
(1)若指数相同而底数不同,则构造幂函数;
(2)若指数不同而底数相同,则构造指数函数;
(3)若指数与底数都不同,则需考虑是否能把指数或底数化为相同,是否可以引入
中间量.
4.4 幂函数
1.了解幂函数的概念、图像及性质,会求幂函数的解析式.
2.通过具体实例,结合y=x,y= ,y=x2,y= ,y=x3的图像,理解它们的变化规律.
3.能利用幂函数的单调性比较大小.
1 |幂函数的概念
一般地,函数① y=xα 称为幂函数,其中α是常数.
2 |五个幂函数的图像与性质
幂函数 y=x y=x2 y=x3 y= y=x-1
图像
性 质 定义域 R R R ② [0,+∞) ③ (-∞,0)
∪(0,+∞)
值域 R ④ [0,+∞)
R [0,+∞) {y|y∈R且y
≠0}
单调性 增 x∈[0,+∞)
增,x∈(-∞,
0)减 增 增 ⑤ x∈(0,+
∞)减,x∈(-
∞,0)减
奇偶性 奇 偶 奇 非奇非偶 奇
公共点 都经过点⑥ (1,1)
判断正误,正确的画“ √” ,错误的画“ ” 。
1.幂函数的图像都过点(0,0),(1,1). ( )
2.幂函数的图像一定不能出现在第四象限,但可能出现在第二象限. ( √ )
3.幂函数在(0,+∞)内不是增函数就是减函数. ( )
4.当α=0时,幂函数y=xα的图像是一条直线.( )
5.指数函数y=ax的定义域为R,与底数a无关,幂函数y=xα的定义域为R,与指数也无
关. ( )
1 |如何把握幂函数的图像
前面我们已熟悉下面几个函数:y= =x-1,y=x,y=x2,y= = .
问题
1.它们有什么结构特点
提示:可从幂的底数与幂指数考虑.
2.在同一坐标系内作出它们的图像并试着总结它们可能具有的性质.
提示:从图像的位置,单调性,对称性,过定点等方面考虑.
解决幂函数图像问题应把握的两个原则:
(1)根据各幂函数在第一象限内的图像确定相应幂指数的大小关系.依据图像高
低判断幂指数大小,相关结论如下:
①在x∈(0,1)上,指数越大,幂函数图像越靠近x轴(简记为指大图低);
②在x∈(1,+∞)上,指数越大,幂函数图像越远离x轴(简记为指大图高).
(2)利用定义域及奇偶性确定函数在其他象限的图像.
(★★☆)若点( ,2)在幂函数f(x)的图像上,点 在幂函数g(x)的图像上,
问当x为何值时,有①f(x)>g(x) ②f(x)=g(x) ③f(x)
先由点在幂函数的图像上确定幂函数的解析式,再由解析式得到大致图像,利用
图像解决问题.
解析 设f(x)=xα(α为常数),因为点( ,2)在幂函数f(x)的图像上,所以将( ,2)代入
f(x)=xα中,得2=( )α,解得α=2,则f(x)=x2.同理,可求得g(x)=x-2.
在同一平面直角坐标系中作出幂函数f(x)=x2和g(x)=x-2的图像(如图所示),
观察图像可得:
①当x>1或x<-1时, f(x)>g(x).②当x=1或x=-1时, f(x)=g(x).③当-1
已知幂函数f(x)= ,其中{m|-2
问题
1.同时满足(1)(2)的幂函数f(x)是否存在
提示:存在.因为{m|-2
由①②③得m=0.因此存在同时满足(1)(2)的幂函数f(x).
2.若存在,如何求出f(x)的解析式,以及x∈[0,3]时f(x)的值域
提示:由问题1知m=0,此时f(x)=x3,且在区间[0,3]上是增函数,所以x∈[0,3]时,函数
f(x)的值域为[0,27].
幂函数的性质与参数α可以互相确定:
(1)幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确
定幂函数的定义域、值域、单调性、奇偶性.
(2)由幂函数的性质可限制α的取值:
①利用幂函数的单调性求出α的取值范围;
②由奇偶性结合其他限制条件确定α的值.
1.(★★☆)已知幂函数y=x3m-9(m∈N*)的图像关于y轴对称,且y=x3m-9(m∈N*)在(0,+
∞)上单调递减,求满足(a+1 < 的实数a的取值范围.
思路点拨:
由函数的性质确定参数m的值,再由函数的单调性解不等式.
解析 因为函数y=x3m-9在(0,+∞)上单调递减,所以3m-9<0,解得m<3.又m∈N*,所以
m=1,2.
因为幂函数y=x3m-9的图像关于y轴对称,所以3m-9为偶数,故m=1,则原不等式可化
为(a+1 <(3-2a .
由y= 在(-∞,0),(0,+∞)上单调递减得,
a+1>3-2a>0或3-2a
(1) 与 ;
(2) 与 ;
(3)0.2 与6.2 ;
(4)0.20.6与0.30.4.
思路点拨:
可以借助幂函数的单调性或中间量进行比较.
解析 (1)∵y= 是[0,+∞)上的增函数,且 > ,
∴ > .
(2)∵y=x-1是(-∞,0)上的减函数,且- <- ,∴ > .
(3)0.2 = = ,6.2 =2. .
∵y= 是[0,+∞)上的增函数,且2<2.5,
∴ <2. ,即0.2 <6.2 .
(4)由幂函数的单调性,知0.20.6<0.30.6,又y=0.3x是减函数,
∴0.30.4>0.30.6,从而0.20.6<0.30.4.
方法总结:
比较幂值的大小,关键在于构造适当的函数:
(1)若指数相同而底数不同,则构造幂函数;
(2)若指数不同而底数相同,则构造指数函数;
(3)若指数与底数都不同,则需考虑是否能把指数或底数化为相同,是否可以引入
中间量.
