2022年新教材高中数学第三章函数1.3函数的奇偶性课件新人教B版必修第一册(共21张PPT)
文档属性
| 名称 | 2022年新教材高中数学第三章函数1.3函数的奇偶性课件新人教B版必修第一册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 458.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:48:54 | ||
图片预览








文档简介
(共21张PPT)
3.1.3 函数的奇偶性
1.了解函数奇偶性的含义.
2.掌握判断函数奇偶性的方法.
3.了解函数奇偶性与图像的对称性之间的关系.
4.熟练运用函数的奇偶性研究函数的其他性质,如单调性.
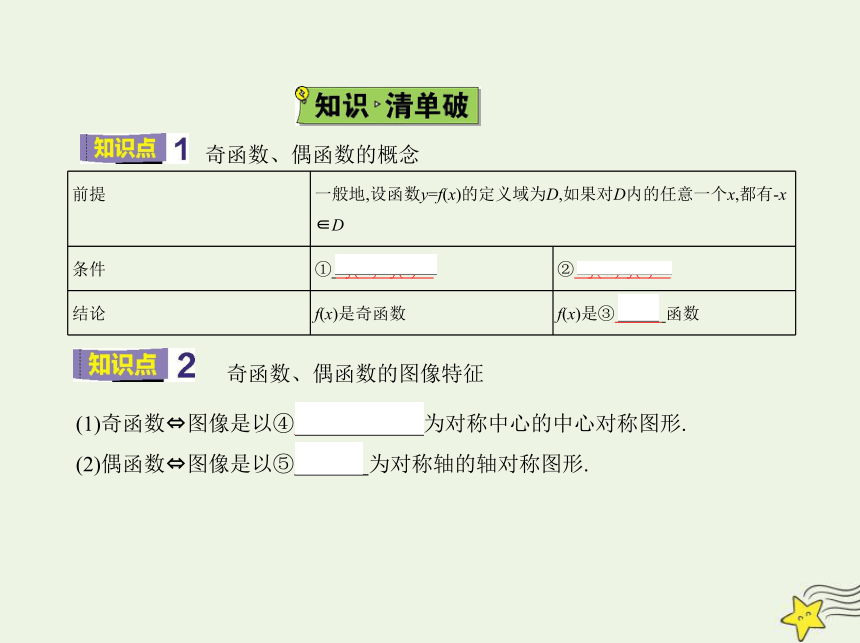
前提 一般地,设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x
∈D
条件 ① f(-x)=-f(x) ② f(-x)=f(x)
结论 f(x)是奇函数 f(x)是③ 偶 函数
奇函数、偶函数的概念
奇函数、偶函数的图像特征
(1)奇函数 图像是以④ 坐标原点 为对称中心的中心对称图形.
(2)偶函数 图像是以⑤ y轴 为对称轴的轴对称图形.
判断正误,正确的画“√”,错误的画“ ”.
1.f(x)是定义在R上的函数.若f(-1)=f(1),则f(x)一定是偶函数. ( )
2.若f(x)为奇函数,则f(0)=0. ( )
3.若f(x)为偶函数,则f(-x)=f(|x|). ( √ )
4.函数y=x2在x∈(0,+∞)上是偶函数. ( )
5.若偶函数的图像不过原点,则它与x轴交点的个数一定是偶数. ( √ )
6.不存在既是奇函数,又是偶函数的函数. ( )
存在,f(x)=0,x∈R既是奇函数,又是偶函数.
7.若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数. ( )
函数f(x)=x2-2x,x∈R的定义域关于原点对称,但它既不是奇函数,也不是偶函数.
已知函数f(x)=(x+1)(x-1),g(x)=x3-x,h(x)= .
问题
1.判断各个函数的奇偶性时,关键要注意什么
提示:注意函数的定义域.
2.函数f(x)= + 的奇偶性是怎样的呢
提示:既是奇函数又是偶函数.
如何判断函数的奇偶性
(2)图像法:
判断函数奇偶性的常见方法
(1)定义法:
分段函数奇偶性的判断
判断分段函数f(x)奇偶性的一般方法是在一个区间上任取自变量,再向对称区间
转化.若函数在x=0处有定义,还要验证f(0),即判断分段函数的奇偶性时必须判断
每一段上函数是否都具有f(-x)=-f(x)或f(-x)=f(x)的特征.也可以作出函数图像结合
对称性判断.
拔高问题
3.定义在R上的函数f(x),对于任意实数a、b都有f(a+b)=f(a)+f(b).如何判断函数f(x)
的奇偶性
提示:令a=b=0 f(0)=0;令a=-x,b=x f(-x)=-f(x).
破疑典例
1.( )判断下列函数的奇偶性:
(1)f(x)= ;
(2)f(x)=|x-2|+|x+2|;
(3)f(x)=
思路点拨:
先求函数的定义域,必要时化简函数解析式,再计算f(-x)并判断f(-x)与f(x)的关系,
从而得出结论.
解析 (1)由1-x2≥0,得-1≤x≤1,又|x+2|-2≠0,∴x≠0,且x≠-4,∴函数f(x)的定义域D={x|-1≤x≤1,且x≠0},
∴函数f(x)的定义域关于原点对称,且x+2>0,
∴f(x)= = ,
于是任取x∈D,都有f(-x)= =- =-f(x),∴f(x)为奇函数.
(2)函数f(x)=|x-2|+|x+2|的定义域为实数集R,关于原点对称.
因为f(-x)=|-x-2|+|-x+2|=|x+2|+|x-2|=|x-2|+|x+2|=f(x),所以函数f(x)=|x-2|+|x+2|是偶函
数.
(3)函数的定义域M=(-∞,0)∪(0,+∞),关于原点对称.
任取x∈M,当x>0时,-x<0,则f(-x)=- = =f(x);
当x<0时,-x>0,则f(-x)= =- =f(x).
综上可知,函数f(x)= 是偶函数.
易错警示 判断奇偶性应先求定义域,必要时在定义域内化简解析式.解题时既
要防止不化简解析式,判断不出f(-x)与f(x)的关系;又要防止不求定义域就化简解
析式,导致不恒等变形得到错误结论.
2.( )设函数f(x)的定义域为(-l,l),证明: f(x)+f(-x)是偶函数,f(x)-f(-x)是奇函数.
思路点拨:
先确定函数的定义域,再利用定义证明奇偶性.
证明 由于x∈(-l,l),因此也必有-x∈(-l,l),所以f(-x)的定义域也是(-l,l).
设F(x)=f(x)+f(-x),G(x)=f(x)-f(-x),
则F(x)与G(x)的定义域也是(-l,l),显然是关于原点对称的.
又F(-x)=f(-x)+f(-(-x))=f(x)+f(-x)=F(x),
G(-x)=f(-x)-f(-(-x))=f(-x)-f(x)=-[f(x)-f(-x)]=-G(x),
所以F(x)为偶函数,G(x)为奇函数,即f(x)+f(-x)是偶函数, f(x)-f(-x)是奇函数.
3.( )定义在R上的函数f(x),对于任意实数x1、x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x
2).判断f(x)的奇偶性.
解析 令x1=0,x2=x,得f(x)+f(-x)=2f(0)·f(x);令x2=0,x1=x,得f(x)+f(x)=2f(0)·f(x).
所以f(x)=f(-x),又f(x)的定义域为R,所以f(x)是偶函数.
函数奇偶性的应用
1.由函数的奇偶性求参数
(1)函数奇偶性的定义既是判断函数奇偶性的一种方法,也是在已知函数奇偶性
时可以运用的一个性质,要注意函数奇偶性定义的正用和逆用.
(2)利用常见函数如一次函数、反比例函数、二次函数具有奇偶性的条件也可求
得参数.
2.根据函数的奇偶性求函数值
利用函数的奇偶性求函数值时,若所给函数具有奇偶性,则利用f(-x)=-f(x)或f(-x)=f
(x)求解;若所给的函数不具有奇偶性,一般需利用所给的函数来构造一个奇函数
或偶函数,然后利用其奇偶性求值.
3.利用奇偶性求函数解析式的一般步骤
(1)在哪个区间上求解析式,x就设在哪个区间.
(2)把x对称转化到已知区间上,利用已知区间的解析式进行代入.
(3)利用函数的奇偶性把f(-x)改写成-f(x)或f(x),从而求出f(x).
破疑典例
1.( )(1)若函数f(x)= 为奇函数,则实数a= ( )
A. B. C. D.1
(2)已知f(x)=x5+ax3+bx-8且f(-2)=10,那么f(2)= .
思路点拨:
(1)利用奇函数的定义得到f(-1)=-f(1),列出方程求出a;
(2)构造出函数g(x)=f(x)+8,易得g(x)为奇函数,由f(-2)=10逐次求出g(-2)、g(2),可求
f(2).
答案 (1)A (2)-26
解析 (1)∵f(x)为奇函数,
∴f(-1)=-f(1),
∴ = ,∴1+a=3(1-a),解得a= ,故选A.
(2)令g(x)=f(x)+8=x5+ax3+bx,易得g(x)为奇函数,
∵f(-2)=10,
∴g(-2)=10+8=18,
∴g(2)=-18,
∴f(2)=g(2)-8=-18-8=-26.
2.( )函数f(x)在R上为奇函数,当x>0时,f(x)= +1,求f(x)的解析式.
思路点拨:
设x<0,则-x>0,结合f(-x)=-f(x),f(0)=0,可求f(x)的解析式.
解析 设x<0,则-x>0,
∴f(-x)= +1,
∵f(x)是R上的奇函数,
∴f(-x)=-f(x),
即-f(x)= +1,
∴f(x)=- -1,
∵f(x)是R上的奇函数,
∴f(0)=0,
∴f(x)=
1.函数的奇偶性与单调性的差异:奇偶性可理解为函数图像在定义域上的对称性,单调性反映函数在某一区间上函数值的变化趋势,奇偶性是相对于函数的
整个定义域来说的,这一点与函数的单调性不同,从这个意义上来讲,函数的单调
性是函数的“局部”性质,而奇偶性是函数的“整体”性质,只有对定义域中的
每一个x,都有f(-x)=-f(x)(f(-x)=f(x)),才说f(x)是奇(偶)函数.
2.奇函数在关于原点对称的区间上单调性相同,偶函数在关于原点对称的区间上
单调性相反.
函数奇偶性与单调性的综合应用
3.区间[a,b]和[-b,-a]关于原点对称.
(1)若f(x)为奇函数,且在[a,b]上有最大值M,则f(x)在[-b,-a]上有最小值-M.
(2)若f(x)为奇函数,f(x)+2在[a,b]上有最大值M,则f(x)+2在[-b,-a]上有最小值-M+4.
4.利用函数的奇偶性与单调性比较函数值的大小,关键是利用奇偶性把自变量转
化到函数的一个单调区间内,然后利用单调性比较.
破疑典例
( )(1)定义在R上的偶函数f(x)满足:对任意的x1、x2∈(-∞,0](x1≠x2),有(x2-x
1)·[ f(x2)-f(x1)]>0,则当n∈N*时,有( )
A.f(-n)B.f(n+1)C.f(n-1)D.f(n+1)(2)若偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1) ;
(3)已知y=f(x)在定义域(-1,1)上是减函数,其图像关于原点对称,且f(1-a)+f(1-2a)<0,
则实数a的取值范围是 .
答案 (1)B (2) (3)
解析 (1)∵对任意的x1、x2∈(-∞,0](x1≠x2),有(x2-x1)·[f(x2)-f(x1)]>0,
∴若x2-x1>0,则f(x2)-f(x1)>0,即若x2>x1,则f(x2)>f(x1);
若x2-x1<0,则f(x2)-f(x1)<0,即若x2则f(x2)∵f(x)在R上是偶函数,∴函数f(x)在[0,+∞)上为单调递减函数,f(-n)=f(n).∵n∈N*,
∴n+1>n>n-1≥0,f(n+1)(2)∵f(x)是偶函数,∴f(x)=f(|x|),∴f(|2x-1|)∵f(x)在[0,+∞)上单调递增,
∴|2x-1|< ,解得(3)∵y=f(x)的图像关于原点对称,∴函数f(x)是奇函数.
∵f(1-a)+f(1-2a)<0,
∴f(1-a)<-f(1-2a)=f(2a-1),又y=f(x)在定义域(-1,1)上是减函数,
∴ 解得0∴a的取值范围是0
3.1.3 函数的奇偶性
1.了解函数奇偶性的含义.
2.掌握判断函数奇偶性的方法.
3.了解函数奇偶性与图像的对称性之间的关系.
4.熟练运用函数的奇偶性研究函数的其他性质,如单调性.
前提 一般地,设函数y=f(x)的定义域为D,如果对D内的任意一个x,都有-x
∈D
条件 ① f(-x)=-f(x) ② f(-x)=f(x)
结论 f(x)是奇函数 f(x)是③ 偶 函数
奇函数、偶函数的概念
奇函数、偶函数的图像特征
(1)奇函数 图像是以④ 坐标原点 为对称中心的中心对称图形.
(2)偶函数 图像是以⑤ y轴 为对称轴的轴对称图形.
判断正误,正确的画“√”,错误的画“ ”.
1.f(x)是定义在R上的函数.若f(-1)=f(1),则f(x)一定是偶函数. ( )
2.若f(x)为奇函数,则f(0)=0. ( )
3.若f(x)为偶函数,则f(-x)=f(|x|). ( √ )
4.函数y=x2在x∈(0,+∞)上是偶函数. ( )
5.若偶函数的图像不过原点,则它与x轴交点的个数一定是偶数. ( √ )
6.不存在既是奇函数,又是偶函数的函数. ( )
存在,f(x)=0,x∈R既是奇函数,又是偶函数.
7.若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数. ( )
函数f(x)=x2-2x,x∈R的定义域关于原点对称,但它既不是奇函数,也不是偶函数.
已知函数f(x)=(x+1)(x-1),g(x)=x3-x,h(x)= .
问题
1.判断各个函数的奇偶性时,关键要注意什么
提示:注意函数的定义域.
2.函数f(x)= + 的奇偶性是怎样的呢
提示:既是奇函数又是偶函数.
如何判断函数的奇偶性
(2)图像法:
判断函数奇偶性的常见方法
(1)定义法:
分段函数奇偶性的判断
判断分段函数f(x)奇偶性的一般方法是在一个区间上任取自变量,再向对称区间
转化.若函数在x=0处有定义,还要验证f(0),即判断分段函数的奇偶性时必须判断
每一段上函数是否都具有f(-x)=-f(x)或f(-x)=f(x)的特征.也可以作出函数图像结合
对称性判断.
拔高问题
3.定义在R上的函数f(x),对于任意实数a、b都有f(a+b)=f(a)+f(b).如何判断函数f(x)
的奇偶性
提示:令a=b=0 f(0)=0;令a=-x,b=x f(-x)=-f(x).
破疑典例
1.( )判断下列函数的奇偶性:
(1)f(x)= ;
(2)f(x)=|x-2|+|x+2|;
(3)f(x)=
思路点拨:
先求函数的定义域,必要时化简函数解析式,再计算f(-x)并判断f(-x)与f(x)的关系,
从而得出结论.
解析 (1)由1-x2≥0,得-1≤x≤1,又|x+2|-2≠0,∴x≠0,且x≠-4,∴函数f(x)的定义域D={x|-1≤x≤1,且x≠0},
∴函数f(x)的定义域关于原点对称,且x+2>0,
∴f(x)= = ,
于是任取x∈D,都有f(-x)= =- =-f(x),∴f(x)为奇函数.
(2)函数f(x)=|x-2|+|x+2|的定义域为实数集R,关于原点对称.
因为f(-x)=|-x-2|+|-x+2|=|x+2|+|x-2|=|x-2|+|x+2|=f(x),所以函数f(x)=|x-2|+|x+2|是偶函
数.
(3)函数的定义域M=(-∞,0)∪(0,+∞),关于原点对称.
任取x∈M,当x>0时,-x<0,则f(-x)=- = =f(x);
当x<0时,-x>0,则f(-x)= =- =f(x).
综上可知,函数f(x)= 是偶函数.
易错警示 判断奇偶性应先求定义域,必要时在定义域内化简解析式.解题时既
要防止不化简解析式,判断不出f(-x)与f(x)的关系;又要防止不求定义域就化简解
析式,导致不恒等变形得到错误结论.
2.( )设函数f(x)的定义域为(-l,l),证明: f(x)+f(-x)是偶函数,f(x)-f(-x)是奇函数.
思路点拨:
先确定函数的定义域,再利用定义证明奇偶性.
证明 由于x∈(-l,l),因此也必有-x∈(-l,l),所以f(-x)的定义域也是(-l,l).
设F(x)=f(x)+f(-x),G(x)=f(x)-f(-x),
则F(x)与G(x)的定义域也是(-l,l),显然是关于原点对称的.
又F(-x)=f(-x)+f(-(-x))=f(x)+f(-x)=F(x),
G(-x)=f(-x)-f(-(-x))=f(-x)-f(x)=-[f(x)-f(-x)]=-G(x),
所以F(x)为偶函数,G(x)为奇函数,即f(x)+f(-x)是偶函数, f(x)-f(-x)是奇函数.
3.( )定义在R上的函数f(x),对于任意实数x1、x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x
2).判断f(x)的奇偶性.
解析 令x1=0,x2=x,得f(x)+f(-x)=2f(0)·f(x);令x2=0,x1=x,得f(x)+f(x)=2f(0)·f(x).
所以f(x)=f(-x),又f(x)的定义域为R,所以f(x)是偶函数.
函数奇偶性的应用
1.由函数的奇偶性求参数
(1)函数奇偶性的定义既是判断函数奇偶性的一种方法,也是在已知函数奇偶性
时可以运用的一个性质,要注意函数奇偶性定义的正用和逆用.
(2)利用常见函数如一次函数、反比例函数、二次函数具有奇偶性的条件也可求
得参数.
2.根据函数的奇偶性求函数值
利用函数的奇偶性求函数值时,若所给函数具有奇偶性,则利用f(-x)=-f(x)或f(-x)=f
(x)求解;若所给的函数不具有奇偶性,一般需利用所给的函数来构造一个奇函数
或偶函数,然后利用其奇偶性求值.
3.利用奇偶性求函数解析式的一般步骤
(1)在哪个区间上求解析式,x就设在哪个区间.
(2)把x对称转化到已知区间上,利用已知区间的解析式进行代入.
(3)利用函数的奇偶性把f(-x)改写成-f(x)或f(x),从而求出f(x).
破疑典例
1.( )(1)若函数f(x)= 为奇函数,则实数a= ( )
A. B. C. D.1
(2)已知f(x)=x5+ax3+bx-8且f(-2)=10,那么f(2)= .
思路点拨:
(1)利用奇函数的定义得到f(-1)=-f(1),列出方程求出a;
(2)构造出函数g(x)=f(x)+8,易得g(x)为奇函数,由f(-2)=10逐次求出g(-2)、g(2),可求
f(2).
答案 (1)A (2)-26
解析 (1)∵f(x)为奇函数,
∴f(-1)=-f(1),
∴ = ,∴1+a=3(1-a),解得a= ,故选A.
(2)令g(x)=f(x)+8=x5+ax3+bx,易得g(x)为奇函数,
∵f(-2)=10,
∴g(-2)=10+8=18,
∴g(2)=-18,
∴f(2)=g(2)-8=-18-8=-26.
2.( )函数f(x)在R上为奇函数,当x>0时,f(x)= +1,求f(x)的解析式.
思路点拨:
设x<0,则-x>0,结合f(-x)=-f(x),f(0)=0,可求f(x)的解析式.
解析 设x<0,则-x>0,
∴f(-x)= +1,
∵f(x)是R上的奇函数,
∴f(-x)=-f(x),
即-f(x)= +1,
∴f(x)=- -1,
∵f(x)是R上的奇函数,
∴f(0)=0,
∴f(x)=
1.函数的奇偶性与单调性的差异:奇偶性可理解为函数图像在定义域上的对称性,单调性反映函数在某一区间上函数值的变化趋势,奇偶性是相对于函数的
整个定义域来说的,这一点与函数的单调性不同,从这个意义上来讲,函数的单调
性是函数的“局部”性质,而奇偶性是函数的“整体”性质,只有对定义域中的
每一个x,都有f(-x)=-f(x)(f(-x)=f(x)),才说f(x)是奇(偶)函数.
2.奇函数在关于原点对称的区间上单调性相同,偶函数在关于原点对称的区间上
单调性相反.
函数奇偶性与单调性的综合应用
3.区间[a,b]和[-b,-a]关于原点对称.
(1)若f(x)为奇函数,且在[a,b]上有最大值M,则f(x)在[-b,-a]上有最小值-M.
(2)若f(x)为奇函数,f(x)+2在[a,b]上有最大值M,则f(x)+2在[-b,-a]上有最小值-M+4.
4.利用函数的奇偶性与单调性比较函数值的大小,关键是利用奇偶性把自变量转
化到函数的一个单调区间内,然后利用单调性比较.
破疑典例
( )(1)定义在R上的偶函数f(x)满足:对任意的x1、x2∈(-∞,0](x1≠x2),有(x2-x
1)·[ f(x2)-f(x1)]>0,则当n∈N*时,有( )
A.f(-n)
(3)已知y=f(x)在定义域(-1,1)上是减函数,其图像关于原点对称,且f(1-a)+f(1-2a)<0,
则实数a的取值范围是 .
答案 (1)B (2) (3)
解析 (1)∵对任意的x1、x2∈(-∞,0](x1≠x2),有(x2-x1)·[f(x2)-f(x1)]>0,
∴若x2-x1>0,则f(x2)-f(x1)>0,即若x2>x1,则f(x2)>f(x1);
若x2-x1<0,则f(x2)-f(x1)<0,即若x2
∴n+1>n>n-1≥0,f(n+1)
∴|2x-1|< ,解得
∵f(1-a)+f(1-2a)<0,
∴f(1-a)<-f(1-2a)=f(2a-1),又y=f(x)在定义域(-1,1)上是减函数,
∴ 解得0
