2022年新教材高中数学第六章平面向量初步1.3向量的减法课件新人教B版必修第二册 课件(共13张PPT)
文档属性
| 名称 | 2022年新教材高中数学第六章平面向量初步1.3向量的减法课件新人教B版必修第二册 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:49:20 | ||
图片预览





文档简介
(共13张PPT)
6.1.3 向量的减法
1.掌握向量减法的运算,并理解其几何意义.
2.理解相反向量的含义,能用相反向量说出向量相减的意义.
3.能将向量的减法运算转化为向量的加法运算.
1 |向量的减法
1.向量的差
一般地,平面上任意给定两个向量a,b,如果向量x能够满足b+x=a,则称x为向量a与
b的差,并记作x=① a-b .
2.向量减法的三角形法则
已知向量a,b,在平面内任取一点O,作 =a, =b,作出向量 ,则 + =
,因此向量 就是向量a与b的差(也称 为向量a与b的差向量),即 - = .
当a与b不共线时,求a-b的差可如图表示,此时向量a,b,a-b正好能构成一个三
角形,因此上述求两向量差的作图方法,也常称为向量减法的三角形法则.
助记法则:共起点,连终点,指被减.
2 |相反向量
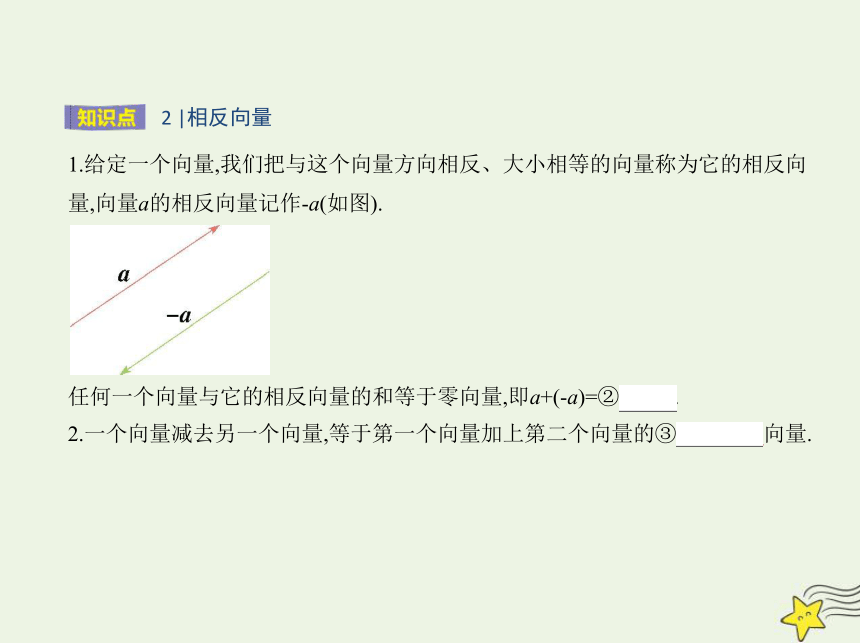
1.给定一个向量,我们把与这个向量方向相反、大小相等的向量称为它的相反向
量,向量a的相反向量记作-a(如图).
任何一个向量与它的相反向量的和等于零向量,即a+(-a)=② 0 .
2.一个向量减去另一个向量,等于第一个向量加上第二个向量的③ 相反 向量.
(1)如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点
为始点,被减向量的终点为终点的向量.
(2)一个向量 等于它的终点相对于点O的位置向量 减去它的始点相对于点O
的位置向量 ,或简记“终点向量减始点向量”.
3 |向量减法的两个重要结论
4 | |a|,|b|与|a-b|的关系
当a与b共线时,如果a,b方向相同,有|a-b|④ = ||a|-|b||;如果a,b反向,则有|a-b|
⑤ = |a|+|b|.
当a,b不共线时,有||a|-|b||⑥ < |a-b|⑦ < |a|+|b|.
判断正误,正确的画“ √” ,错误的画“ ” 。
1. = - . ( √ )
2.若b是a的相反向量,则a与b一定不相等. ( )
3.|a|-|b|≤|a|+|b|. ( √ )
4. - = . ( )
5.两个同向向量的差一定小于这两个向量的和. ( )
1 |利用已知向量表示其他向量
用已知向量表示其他向量的一般步骤
(1)先观察各个向量在图形中的位置.
(2)寻找(或作出)相应的平行四边形或三角形.
(3)运用法则找关系.
(4)化简结果.
利用已知向量表示其他向量的一个关键及两个注意点
(1)一个关键:
确定已知向量与被表示向量的转化渠道.
(2)两个注意点:
①注意相等向量、相反向量、共线向量以及构成三角形的三个向量之间的关系;
②注意应用向量的加法、减法的几何意义以及向量加法的运算律.
(★★☆)如图,解答下列问题:
(1)用a,d,e表示 ;
(2)用b,c表示 ;
(3)用a,b,e表示 ;
(4)用d,c表示 .
思路点拨:
选择一个向量起点到终点的路线 用已知向量表示出来.
解析 由题图可知: =a, =b, =c, =d, =e.
(1) = + + =d+e+a.
(2) = + =-c-b.
(3) = + + =e+a+b.
(4) = + =- - =-d-c.
2|向量的加、减混合运算
1.掌握向量加、减法的定义及向量加法的交换律、结合律等基础知识,在求解时
将杂乱的向量运算式有序化处理,常用的变形有三种:
(1)化减为加,即运用 =- 或 + =0.
(2)“首尾顺次相接的形式相加”,即运用 + = .
(3)“同一点出发的两个向量的差”,即运用 - = 或 = - .
2.以向量 =a, =b为邻边作平行四边形ABCD,则两条对角线向量分别为 =a
+b, =a-b,如图所示,这一结论的应用非常广泛.
1.(★☆☆)化简:(1)( - )-( - );
(2)( + + )-( - - ).
思路点拨:
根据向量加、减法的定义,结合向量加法的交换律、结合律化简.
解析 (1)( - )-( - )=( + )-( + )= - =0.
(2)( + + )-( - - )=( + )-( - )= - =0.
2.(★★☆)若O是△ABC所在平面内一点,且满足| - |=| - + - |,证明
△ABC是直角三角形.
证明 因为 - + - = + , - = = - ,
又| - |=| - + - |,
所以| - |=| + |,
所以以AB,AC为邻边的平行四边形的两条对角线的长度相等,所以此平行四边形
为矩形,
所以AB⊥AC,所以△ABC是直角三角形.
方法总结:用向量法解决平面几何问题的步骤:
①将平面几何问题中的量抽象成向量.
②转化为向量问题,进行向量运算.
③将向量问题还原为平面几何问题.
6.1.3 向量的减法
1.掌握向量减法的运算,并理解其几何意义.
2.理解相反向量的含义,能用相反向量说出向量相减的意义.
3.能将向量的减法运算转化为向量的加法运算.
1 |向量的减法
1.向量的差
一般地,平面上任意给定两个向量a,b,如果向量x能够满足b+x=a,则称x为向量a与
b的差,并记作x=① a-b .
2.向量减法的三角形法则
已知向量a,b,在平面内任取一点O,作 =a, =b,作出向量 ,则 + =
,因此向量 就是向量a与b的差(也称 为向量a与b的差向量),即 - = .
当a与b不共线时,求a-b的差可如图表示,此时向量a,b,a-b正好能构成一个三
角形,因此上述求两向量差的作图方法,也常称为向量减法的三角形法则.
助记法则:共起点,连终点,指被减.
2 |相反向量
1.给定一个向量,我们把与这个向量方向相反、大小相等的向量称为它的相反向
量,向量a的相反向量记作-a(如图).
任何一个向量与它的相反向量的和等于零向量,即a+(-a)=② 0 .
2.一个向量减去另一个向量,等于第一个向量加上第二个向量的③ 相反 向量.
(1)如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点
为始点,被减向量的终点为终点的向量.
(2)一个向量 等于它的终点相对于点O的位置向量 减去它的始点相对于点O
的位置向量 ,或简记“终点向量减始点向量”.
3 |向量减法的两个重要结论
4 | |a|,|b|与|a-b|的关系
当a与b共线时,如果a,b方向相同,有|a-b|④ = ||a|-|b||;如果a,b反向,则有|a-b|
⑤ = |a|+|b|.
当a,b不共线时,有||a|-|b||⑥ < |a-b|⑦ < |a|+|b|.
判断正误,正确的画“ √” ,错误的画“ ” 。
1. = - . ( √ )
2.若b是a的相反向量,则a与b一定不相等. ( )
3.|a|-|b|≤|a|+|b|. ( √ )
4. - = . ( )
5.两个同向向量的差一定小于这两个向量的和. ( )
1 |利用已知向量表示其他向量
用已知向量表示其他向量的一般步骤
(1)先观察各个向量在图形中的位置.
(2)寻找(或作出)相应的平行四边形或三角形.
(3)运用法则找关系.
(4)化简结果.
利用已知向量表示其他向量的一个关键及两个注意点
(1)一个关键:
确定已知向量与被表示向量的转化渠道.
(2)两个注意点:
①注意相等向量、相反向量、共线向量以及构成三角形的三个向量之间的关系;
②注意应用向量的加法、减法的几何意义以及向量加法的运算律.
(★★☆)如图,解答下列问题:
(1)用a,d,e表示 ;
(2)用b,c表示 ;
(3)用a,b,e表示 ;
(4)用d,c表示 .
思路点拨:
选择一个向量起点到终点的路线 用已知向量表示出来.
解析 由题图可知: =a, =b, =c, =d, =e.
(1) = + + =d+e+a.
(2) = + =-c-b.
(3) = + + =e+a+b.
(4) = + =- - =-d-c.
2|向量的加、减混合运算
1.掌握向量加、减法的定义及向量加法的交换律、结合律等基础知识,在求解时
将杂乱的向量运算式有序化处理,常用的变形有三种:
(1)化减为加,即运用 =- 或 + =0.
(2)“首尾顺次相接的形式相加”,即运用 + = .
(3)“同一点出发的两个向量的差”,即运用 - = 或 = - .
2.以向量 =a, =b为邻边作平行四边形ABCD,则两条对角线向量分别为 =a
+b, =a-b,如图所示,这一结论的应用非常广泛.
1.(★☆☆)化简:(1)( - )-( - );
(2)( + + )-( - - ).
思路点拨:
根据向量加、减法的定义,结合向量加法的交换律、结合律化简.
解析 (1)( - )-( - )=( + )-( + )= - =0.
(2)( + + )-( - - )=( + )-( - )= - =0.
2.(★★☆)若O是△ABC所在平面内一点,且满足| - |=| - + - |,证明
△ABC是直角三角形.
证明 因为 - + - = + , - = = - ,
又| - |=| - + - |,
所以| - |=| + |,
所以以AB,AC为邻边的平行四边形的两条对角线的长度相等,所以此平行四边形
为矩形,
所以AB⊥AC,所以△ABC是直角三角形.
方法总结:用向量法解决平面几何问题的步骤:
①将平面几何问题中的量抽象成向量.
②转化为向量问题,进行向量运算.
③将向量问题还原为平面几何问题.
