2022年新教材高中数学第六章平面向量初步1.2向量的加法课件新人教B版必修第二册(共16张PPT)
文档属性
| 名称 | 2022年新教材高中数学第六章平面向量初步1.2向量的加法课件新人教B版必修第二册(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:55:30 | ||
图片预览





文档简介
(共16张PPT)
1.掌握向量加法的运算,并理解其几何意义.
2.理解向量加法的三角形法则、平行四边形法则的适用范围,并能应用向量加法
的运算律进行相关运算.
6.1.2 向量的加法
1 |向量加法的三角形法则
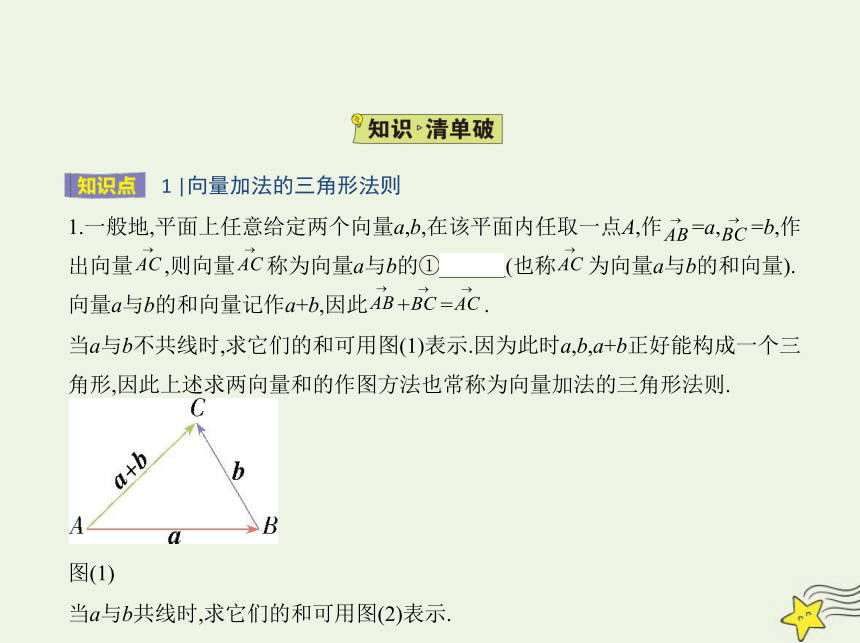
1.一般地,平面上任意给定两个向量a,b,在该平面内任取一点A,作 =a, =b,作
出向量 ,则向量 称为向量a与b的① 和 (也称 为向量a与b的和向量).
向量a与b的和向量记作a+b,因此 + = .
当a与b不共线时,求它们的和可用图(1)表示.因为此时a,b,a+b正好能构成一个三
角形,因此上述求两向量和的作图方法也常称为向量加法的三角形法则.
图(1)
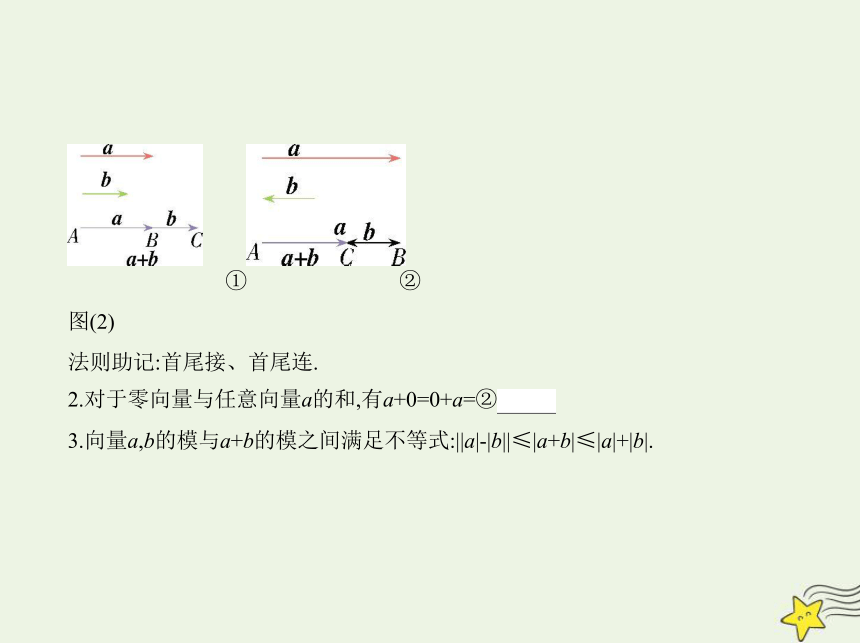
当a与b共线时,求它们的和可用图(2)表示.
① ②
图(2)
法则助记:首尾接、首尾连.
2.对于零向量与任意向量a的和,有a+0=0+a=② a .
3.向量a,b的模与a+b的模之间满足不等式:||a|-|b||≤|a+b|≤|a|+|b|.
如图所示,平面上任意给定两个不共线的向量a,b,在该平面内任取一点A,作
=a, =b,以AB,AC为邻边作一个平行四边形ABDC,作出向量 ,因为 =
,所以 = + = + .
这种求两向量和的作图方法也常称为向量加法的平行四边形法则.
法则助记:共起点,对角线.
2 |向量加法的平行四边形法则
(1)交换律:a+b=b+a;
(2)结合律:(a+b)+c=a+③ (b+c) .
3 |向量加法的运算律
4 |多个向量相加
已知n个向量,依次把这n个向量首尾相连,以第一个向量的始点为始点,第n个
向量的终点为终点的向量就是这n个向量的和向量.
法则助记:首尾接,首尾连.
判断正误,正确的画“ √” ,错误的画“ ” 。
1.两个向量的和可能是数量. ( )
2.两个向量相加就是它们的模相加. ( )
提示:因为向量既有大小,又有方向,所以两个向量相加不是模的相加.
3. + + + + + =0. ( )
4.若a,b均为非零向量,则|a+b|与|a|+|b|一定相等. ( )
5.求任意两个非零向量的和都可以用平行四边形法则. ( )
1 |准确使用向量的加法法则和运算律
雨滴在下落一定时间后的运动是匀速的,无风时雨滴下落的速度是4.0 m/s,现在
有风,风使雨滴以 m/s的水平速度向东移动.
问题
1.雨滴着地时速度方向如何用示意图画出
提示:如图,用 表示雨滴下落的速度, 表示风使雨滴水平向东的速度,以 ,
为邻边作平行四边形OACB, 就是雨滴下落的实际方向和速度.
2.如何求雨滴落地时的实际速度大小
提示:雨滴着地时的速度大小是 m/s.
3.雨滴落地时的方向如何描述
提示:方向向东且与竖直方向成30°角.
1.三角形法则和平行四边形法则的适用条件
三角形法则和平行四边形法则都只适用于两个不共线的向量求和.
重要提示 应用三角形法则和平行四边形法则应注意的问题:在使用向量加法的
三角形法则时,要注意“首尾相接”,即第一个向量的终点与第二个向量的起点重合,则以第一个向量的起点为起点,并以第二个向量的终点为终点的向量为两向量的和;向量加法的平行四边形法则的应用前提是“共起点”,即两个向量是从同一点出发的不共线向量.
2.已知n个向量,把这n个向量首尾顺次相连,以第一个向量的起点为起点,第n个向
量的终点为终点的向量叫做这n个向量的和向量,这个法则叫做向量求和的多边
形法则.当首尾顺次相连的若干个向量构成封闭的向量链时,各个向量的和为0.
如图所示,在n边形A1A2…An中,有 + +…+ = ,则 + +…+
+ =0.
向量加法的运算律
1.交换律提示我们,多个向量求和时,其顺序可以随便调整.
2.结合律提示我们,可将易运算的两个向量相加,再进行其他运算.
1.(★☆☆)化简下列各式.
(1) + + ;
(2) + + + + .
思路点拨:
利用三角形法则化简,注意“首尾相接”以及运算律的应用.
解析 (1) + + =( + )+ = + = .
(2) + + + + =( + )+( + )+ = + + = + =0.
2.(★☆☆)如下图,在正六边形OABCDE中,若 =a, =b,试用向量a,b将 , ,
表示出来.
思路点拨:
利用向量加法的三角形法则和平行四边形法则求解即可.
解析 由题意知四边形ABPO,AOEP均为平行四边形,
由向量的平行四边形法则,知 = + =a+b.
∵ = ,∴ =a+b.
在△AOB中,根据向量的三角形法则,知 = + =a+a+b=2a+b,
∴ = + =2a+b+b=2a+2b.
= + = + =b+a+b=a+2b.
误区警示:利用平行四边形法则时,必须把两个向量移到同一起点;利用三角形法
则时,两个向量中第二个向量的起点必须是第一个向量的终点.
2|向量加法的几何意义的应用
1.向量加法的三角形法则和平行四边形法则就是向量加法的几何意义.当两个向
量不共线时,三角形法则和平行四边形法则实质是一样的.由三角形法则作出的
图形是由平行四边形法则作出的图形的一半.
2.在图形中作出(或找出)平行四边形或三角形是求解向量加法的几何意义的应
用问题的关键,此类问题考查了逻辑推理、直观想象的核心素养.
(★★☆)如图所示,P,Q是△ABC的边BC上两点,且 + =0.
求证: + = + .
思路点拨:
先找到图形中的三角形,再灵活应用法则求解.
证明 因为 = + , = + ,
所以 + = + + + .
又因为 + =0,所以 + = + .
1.掌握向量加法的运算,并理解其几何意义.
2.理解向量加法的三角形法则、平行四边形法则的适用范围,并能应用向量加法
的运算律进行相关运算.
6.1.2 向量的加法
1 |向量加法的三角形法则
1.一般地,平面上任意给定两个向量a,b,在该平面内任取一点A,作 =a, =b,作
出向量 ,则向量 称为向量a与b的① 和 (也称 为向量a与b的和向量).
向量a与b的和向量记作a+b,因此 + = .
当a与b不共线时,求它们的和可用图(1)表示.因为此时a,b,a+b正好能构成一个三
角形,因此上述求两向量和的作图方法也常称为向量加法的三角形法则.
图(1)
当a与b共线时,求它们的和可用图(2)表示.
① ②
图(2)
法则助记:首尾接、首尾连.
2.对于零向量与任意向量a的和,有a+0=0+a=② a .
3.向量a,b的模与a+b的模之间满足不等式:||a|-|b||≤|a+b|≤|a|+|b|.
如图所示,平面上任意给定两个不共线的向量a,b,在该平面内任取一点A,作
=a, =b,以AB,AC为邻边作一个平行四边形ABDC,作出向量 ,因为 =
,所以 = + = + .
这种求两向量和的作图方法也常称为向量加法的平行四边形法则.
法则助记:共起点,对角线.
2 |向量加法的平行四边形法则
(1)交换律:a+b=b+a;
(2)结合律:(a+b)+c=a+③ (b+c) .
3 |向量加法的运算律
4 |多个向量相加
已知n个向量,依次把这n个向量首尾相连,以第一个向量的始点为始点,第n个
向量的终点为终点的向量就是这n个向量的和向量.
法则助记:首尾接,首尾连.
判断正误,正确的画“ √” ,错误的画“ ” 。
1.两个向量的和可能是数量. ( )
2.两个向量相加就是它们的模相加. ( )
提示:因为向量既有大小,又有方向,所以两个向量相加不是模的相加.
3. + + + + + =0. ( )
4.若a,b均为非零向量,则|a+b|与|a|+|b|一定相等. ( )
5.求任意两个非零向量的和都可以用平行四边形法则. ( )
1 |准确使用向量的加法法则和运算律
雨滴在下落一定时间后的运动是匀速的,无风时雨滴下落的速度是4.0 m/s,现在
有风,风使雨滴以 m/s的水平速度向东移动.
问题
1.雨滴着地时速度方向如何用示意图画出
提示:如图,用 表示雨滴下落的速度, 表示风使雨滴水平向东的速度,以 ,
为邻边作平行四边形OACB, 就是雨滴下落的实际方向和速度.
2.如何求雨滴落地时的实际速度大小
提示:雨滴着地时的速度大小是 m/s.
3.雨滴落地时的方向如何描述
提示:方向向东且与竖直方向成30°角.
1.三角形法则和平行四边形法则的适用条件
三角形法则和平行四边形法则都只适用于两个不共线的向量求和.
重要提示 应用三角形法则和平行四边形法则应注意的问题:在使用向量加法的
三角形法则时,要注意“首尾相接”,即第一个向量的终点与第二个向量的起点重合,则以第一个向量的起点为起点,并以第二个向量的终点为终点的向量为两向量的和;向量加法的平行四边形法则的应用前提是“共起点”,即两个向量是从同一点出发的不共线向量.
2.已知n个向量,把这n个向量首尾顺次相连,以第一个向量的起点为起点,第n个向
量的终点为终点的向量叫做这n个向量的和向量,这个法则叫做向量求和的多边
形法则.当首尾顺次相连的若干个向量构成封闭的向量链时,各个向量的和为0.
如图所示,在n边形A1A2…An中,有 + +…+ = ,则 + +…+
+ =0.
向量加法的运算律
1.交换律提示我们,多个向量求和时,其顺序可以随便调整.
2.结合律提示我们,可将易运算的两个向量相加,再进行其他运算.
1.(★☆☆)化简下列各式.
(1) + + ;
(2) + + + + .
思路点拨:
利用三角形法则化简,注意“首尾相接”以及运算律的应用.
解析 (1) + + =( + )+ = + = .
(2) + + + + =( + )+( + )+ = + + = + =0.
2.(★☆☆)如下图,在正六边形OABCDE中,若 =a, =b,试用向量a,b将 , ,
表示出来.
思路点拨:
利用向量加法的三角形法则和平行四边形法则求解即可.
解析 由题意知四边形ABPO,AOEP均为平行四边形,
由向量的平行四边形法则,知 = + =a+b.
∵ = ,∴ =a+b.
在△AOB中,根据向量的三角形法则,知 = + =a+a+b=2a+b,
∴ = + =2a+b+b=2a+2b.
= + = + =b+a+b=a+2b.
误区警示:利用平行四边形法则时,必须把两个向量移到同一起点;利用三角形法
则时,两个向量中第二个向量的起点必须是第一个向量的终点.
2|向量加法的几何意义的应用
1.向量加法的三角形法则和平行四边形法则就是向量加法的几何意义.当两个向
量不共线时,三角形法则和平行四边形法则实质是一样的.由三角形法则作出的
图形是由平行四边形法则作出的图形的一半.
2.在图形中作出(或找出)平行四边形或三角形是求解向量加法的几何意义的应
用问题的关键,此类问题考查了逻辑推理、直观想象的核心素养.
(★★☆)如图所示,P,Q是△ABC的边BC上两点,且 + =0.
求证: + = + .
思路点拨:
先找到图形中的三角形,再灵活应用法则求解.
证明 因为 = + , = + ,
所以 + = + + + .
又因为 + =0,所以 + = + .
