2022年新教材高中数学第二章等式与不等式2.4均值不等式及其应用课件新人教B版必修第一册(共21张PPT)
文档属性
| 名称 | 2022年新教材高中数学第二章等式与不等式2.4均值不等式及其应用课件新人教B版必修第一册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 582.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:56:06 | ||
图片预览







文档简介
(共21张PPT)
2.2.4 均值不等式及其应用
1.了解均值不等式的代数和几何背景,掌握均值不等式的适用条件.
2.能用均值不等式求最值.
3.能够用均值不等式证明不等式.
4.能用均值不等式解决一些实际问题中的最值问题.
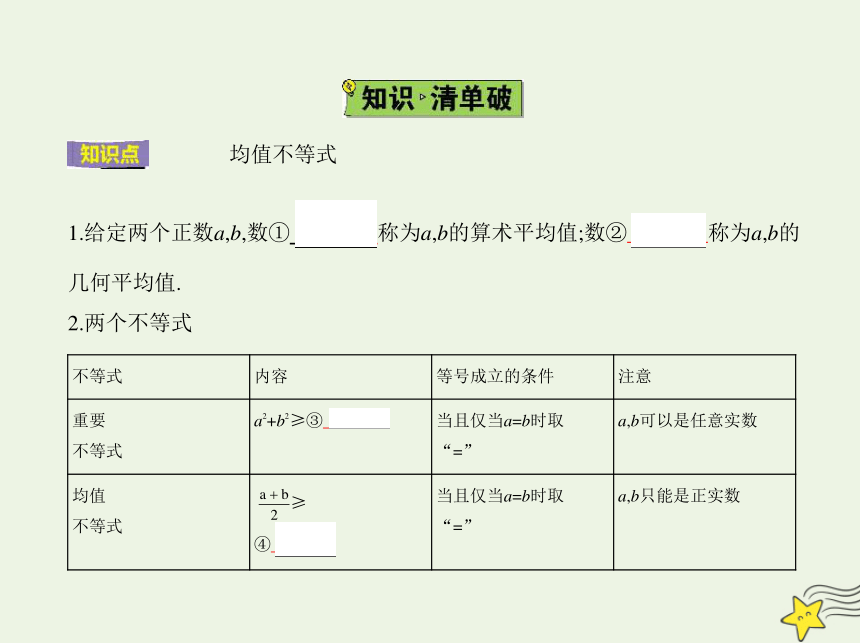
均值不等式
1.给定两个正数a,b,数① 称为a,b的算术平均值;数② 称为a,b的
几何平均值.
2.两个不等式
不等式 内容 等号成立的条件 注意
重要 不等式 a2+b2≥③ 2ab 当且仅当a=b时取
“=” a,b可以是任意实数
均值 不等式 ≥ ④ 当且仅当a=b时取
“=” a,b只能是正实数
3.均值不等式与最值
(1)已知x,y均为正实数,如果积xy是定值p,那么当x=y时,和x+y有最小值,最小值为
⑤ 2 .
(2)已知x,y均为正实数,如果和x+y是定值S,那么当x=y时,积xy有最大值,最大值为
⑥ .
上述命题可归纳为口诀:积定和最小,和定积最大.
运用以上结论求最值要注意下列三个条件:
①一正:要求各数均为⑦ 正数 ;
②二定:要求和或积为⑧ 定值 ;
③三相等:要保证具备⑨ 等号 成立的条件.
判断正误,正确的画“√”,错误的画“ ”.
1.不等式a2+b2≥2ab与 ≤ 有相同的适用范围. ( )
不等式a2+b2≥2ab对任意实数a,b都成立,而 ≤ 只有当a,b都是正实数(特
殊时可取0)时成立.
2.已知m>0,n>0,且mn=81,则m+n的最小值为18.( √ )
因为m>0,n>0,所以m+n≥2 =2 =18,当且仅当m=n=9时取等号,故m+n的最小
值为18.
3.a+ 的最小值为2. ( )
当a>0时,a+ ≥2 =2;当a<0时,(-a)+ ≥2,∴a+ ≤-2.
4.x2+ 的最小值为0. ( )
等号不成立.
5.已知a>0,b>0,则 ≥4. ( √ )
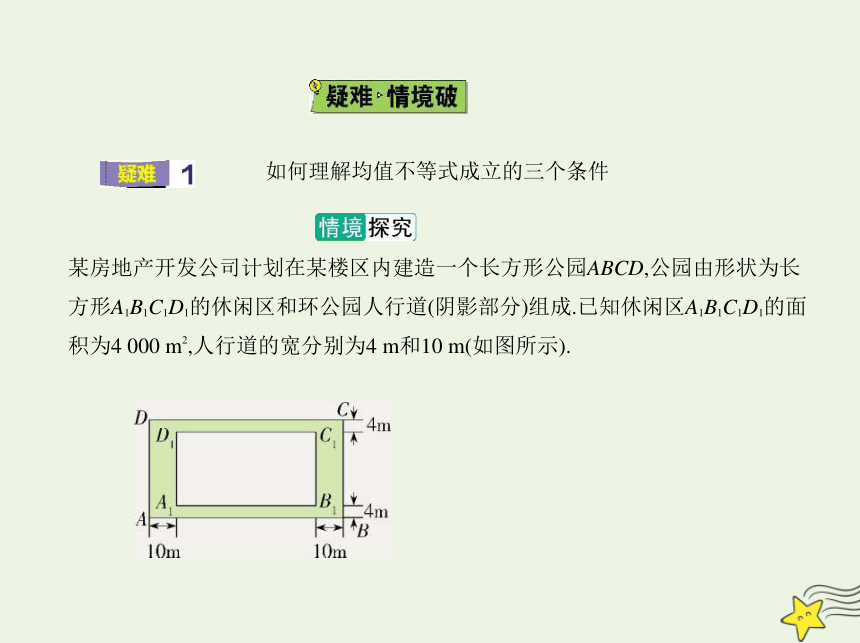
某房地产开发公司计划在某楼区内建造一个长方形公园ABCD,公园由形状为长
方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面
积为4 000 m2,人行道的宽分别为4 m和10 m(如图所示).
如何理解均值不等式成立的三个条件
问题
1.设休闲区的长和宽的比 =x(x>1),求公园ABCD所占面积y关于x的函数关系
式.
提示:y=80 +4 160(x>1).
2.要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计
提示:利用均值不等式求解.
利用均值不等式求最值时的注意事项
1.各项均为正,都是负数时它们的相反数为正.
2.寻求定值,求和式最小值时应使积为定值,求积式最大值时应使和为定值.
3.考虑等号成立的条件是否具备,等号不成立时可用图像找出最大(小)值.函数y=x
+ (a>0)的大致图像如图:
拔高问题
3.若x<0,如何求函数y=x+ 的最大值
提示:当x<0时,-x>0,-x+ ≥2 =4,∴x+ ≤-4,当且仅当-x=- ,即x=-2(x=2
舍去)时取等号.故所求函数的最大值为-4.
4.已知x>2,如何求x+ 的最小值
提示:∵x>2,∴x-2>0,
∴x+ =x-2+ +2≥2 +2=6,当且仅当x-2= ,即x=4(x=0舍去)
时,等号成立.
∴x+ 的最小值为6.
5.若x≥3,如何求函数y=x+ 的最小值
提示:若x>0,则y=x+ ≥2 =4,当且仅当x=2时取得最小值4,函数图像如图所
示.
由图像知,若x≥3,则当x=3时,y取得最小值 .
破疑典例
1.( )已知x<3,求y= +x的最大值.
思路点拨:
x-3<0,则3-x>0,利用均值不等式求y= +x的最大值.
解析 ∵x<3,∴x-3<0,∴3-x>0,
∴y= +x= +x-3+3
=- +3
≤-2 +3=-1,
当且仅当 =3-x,即x=1时,取等号,∴y的最大值为-1.
易错警示 解题时要注意不等号的方向,如由a+b≥2 ,得-(a+b)≤-2 ,防止
不等号方向错误导致解题错误.
2.( )已知x>-1,求函数y= 的最小值.
思路点拨:
将x+1看成整体,将函数化为整式+分式的形式,即构造能利用均值不等式的形式,
检验三个条件是否成立,再求最小值.
解析 ∵x>-1,∴x+1>0,
∴y=
=
=x+1+ +5≥2 +5=9,
当且仅当x+1= ,即x=1(x=-3舍去)时,等号成立.
∴当x=1时,函数y= (x>-1)取得最小值9.
3.( )若x>1,求函数y=x+ + 的最小值.
思路点拨:
思路一:将 变形为 ,然后把x+ 看作一个整体进行求解.
思路二:当涉及分数时,通分是最容易想到的常规方法,通分后x+ = ,利用均
值不等式即可求解.
解析 解法一:y=x+ + =x+ + ,令u=x+ ,则u>2,所以y=u+ ≥8,当且仅
当u= ,即u=4时,此时x=2+ ,等号成立.
解法二:y=x+ + = + ≥2 =8,当且仅当 = ,即x=
2+ 时,等号成立.
4.( )已知a>b>0,求a2+ 的最小值.
思路点拨:
分析目标式的特点,对目标式进行适当变形,然后利用均值不等式求最小值.
解析 解法一:由于a2+ 中有两个字母,并注意到b+(a-b)=a,则b(a-b)≤
= ,这样就消去了字母b,因此a2+ ≥a2+ ≥4,当且仅当b=a-b,a
2= ,即a= ,b= 时,等号成立.故a2+ 的最小值为4.
解法二:注意到b+(a-b)=a,则[b+(a-b)]2=a2,则a2+ =[b+(a-b)]2+ ≥4b(a-
b)+ ≥4,当且仅当b=a-b,4b(a-b)= ,即a= ,b= 时,等号成立.故a2+
的最小值为4.
已知x>0,y>0,且 + =1.
问题
1.怎样求x+y的最小值
提示:消元法或利用均值不等式求解.
2.若将已知条件改为xy≠0,且 + =1,怎样求x+y的最小值
提示:先消元,再利用均值不等式求解.
利用均值不等式解决条件求值问题
求含有条件的最大(小)值的基本方法
1.代入消去一个变量,化为求只含一个变量的代数式的最大(小)值问题,解题时要
注意将消去变量的取值范围转化到保留的变量中.
2.分析条件与结论的关系,利用关系解题,这种方法运算量小但技巧性强,平时要多总结.例如:
常数代换:这种方法常用于“已知ax+by=m(a,b,x,y均为正数),求 + 的最小值”
和“已知 + =1(a,b,x,y均为正数),求x+y的最小值”两种类型.
破疑典例
1.( )已知a>0,b>0,若不等式 + ≥ 恒成立,则m的最大值为 ( )
A.9 B.12 C.18 D.24
思路点拨:
先将不等式变形,再利用均值不等式求解.
B 因为a>0,b>0,不等式 + ≥ 恒成立,所以m≤ .
因为(a+3b) =6+ + ≥6+2 =12,
当且仅当a=3b时取等号,所以m的最大值为12.故选B.
2.( )(1)已知a,b,x,y均为正数,且 + =1,求x+y的最小值;
(2)已知x>0,y>0,且x+2y+xy=30,求xy的最大值.
思路点拨:
问题(1)既可以采用常数代换的方法,也可以进行变量代换,再利用均值不等式求
解;问题(2)既可以利用均值不等式求解,也可以采用变量代换的方法求解.
解析 (1)解法一:x+y=(x+y)· =a+b+ + ≥a+b+2 ,当且仅当
即 时,等号成立,故x+y的最小值为a+b+2 .
解法二:由 + =1得x= ,
∴x+y= +y= +y
=a+ +y= +(y-b)+a+b.
∵x>0,y>0,a>0,∴由 >0得y-b>0,∴x+y≥2 +a+b,
当且仅当
即 时,等号成立,故x+y的最小值为a+b+2 .
(2)解法一:由x+2y+xy=30,可得y= (0xy=
=
=34- ,
注意到x+2+ ≥2· =16,可得xy≤18,
当且仅当x+2= ,即x=6时,等号成立,代入x+2y+xy=30中得y=3,故xy的最大值为
18.
解法二:∵x,y>0,∴x+2y≥2 =2 · ,
∴2 · +xy≤x+2y+xy=30,
解此不等式得0≤xy≤18,即xy的最大值为18,此时 即
3.( )已知x,y,z为正实数且满足x-2y+3z=0,求 的最小值.
思路点拨:
由已知得y= 代入 利用均值不等式求最小值.
解析 由x-2y+3z=0,得y= .因为x,y,z为正实数,所以 = = + +6 ≥ 2 +6 =3,当且仅当x=3z时,等号成立,故 的最小值为3.
2.2.4 均值不等式及其应用
1.了解均值不等式的代数和几何背景,掌握均值不等式的适用条件.
2.能用均值不等式求最值.
3.能够用均值不等式证明不等式.
4.能用均值不等式解决一些实际问题中的最值问题.
均值不等式
1.给定两个正数a,b,数① 称为a,b的算术平均值;数② 称为a,b的
几何平均值.
2.两个不等式
不等式 内容 等号成立的条件 注意
重要 不等式 a2+b2≥③ 2ab 当且仅当a=b时取
“=” a,b可以是任意实数
均值 不等式 ≥ ④ 当且仅当a=b时取
“=” a,b只能是正实数
3.均值不等式与最值
(1)已知x,y均为正实数,如果积xy是定值p,那么当x=y时,和x+y有最小值,最小值为
⑤ 2 .
(2)已知x,y均为正实数,如果和x+y是定值S,那么当x=y时,积xy有最大值,最大值为
⑥ .
上述命题可归纳为口诀:积定和最小,和定积最大.
运用以上结论求最值要注意下列三个条件:
①一正:要求各数均为⑦ 正数 ;
②二定:要求和或积为⑧ 定值 ;
③三相等:要保证具备⑨ 等号 成立的条件.
判断正误,正确的画“√”,错误的画“ ”.
1.不等式a2+b2≥2ab与 ≤ 有相同的适用范围. ( )
不等式a2+b2≥2ab对任意实数a,b都成立,而 ≤ 只有当a,b都是正实数(特
殊时可取0)时成立.
2.已知m>0,n>0,且mn=81,则m+n的最小值为18.( √ )
因为m>0,n>0,所以m+n≥2 =2 =18,当且仅当m=n=9时取等号,故m+n的最小
值为18.
3.a+ 的最小值为2. ( )
当a>0时,a+ ≥2 =2;当a<0时,(-a)+ ≥2,∴a+ ≤-2.
4.x2+ 的最小值为0. ( )
等号不成立.
5.已知a>0,b>0,则 ≥4. ( √ )
某房地产开发公司计划在某楼区内建造一个长方形公园ABCD,公园由形状为长
方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面
积为4 000 m2,人行道的宽分别为4 m和10 m(如图所示).
如何理解均值不等式成立的三个条件
问题
1.设休闲区的长和宽的比 =x(x>1),求公园ABCD所占面积y关于x的函数关系
式.
提示:y=80 +4 160(x>1).
2.要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计
提示:利用均值不等式求解.
利用均值不等式求最值时的注意事项
1.各项均为正,都是负数时它们的相反数为正.
2.寻求定值,求和式最小值时应使积为定值,求积式最大值时应使和为定值.
3.考虑等号成立的条件是否具备,等号不成立时可用图像找出最大(小)值.函数y=x
+ (a>0)的大致图像如图:
拔高问题
3.若x<0,如何求函数y=x+ 的最大值
提示:当x<0时,-x>0,-x+ ≥2 =4,∴x+ ≤-4,当且仅当-x=- ,即x=-2(x=2
舍去)时取等号.故所求函数的最大值为-4.
4.已知x>2,如何求x+ 的最小值
提示:∵x>2,∴x-2>0,
∴x+ =x-2+ +2≥2 +2=6,当且仅当x-2= ,即x=4(x=0舍去)
时,等号成立.
∴x+ 的最小值为6.
5.若x≥3,如何求函数y=x+ 的最小值
提示:若x>0,则y=x+ ≥2 =4,当且仅当x=2时取得最小值4,函数图像如图所
示.
由图像知,若x≥3,则当x=3时,y取得最小值 .
破疑典例
1.( )已知x<3,求y= +x的最大值.
思路点拨:
x-3<0,则3-x>0,利用均值不等式求y= +x的最大值.
解析 ∵x<3,∴x-3<0,∴3-x>0,
∴y= +x= +x-3+3
=- +3
≤-2 +3=-1,
当且仅当 =3-x,即x=1时,取等号,∴y的最大值为-1.
易错警示 解题时要注意不等号的方向,如由a+b≥2 ,得-(a+b)≤-2 ,防止
不等号方向错误导致解题错误.
2.( )已知x>-1,求函数y= 的最小值.
思路点拨:
将x+1看成整体,将函数化为整式+分式的形式,即构造能利用均值不等式的形式,
检验三个条件是否成立,再求最小值.
解析 ∵x>-1,∴x+1>0,
∴y=
=
=x+1+ +5≥2 +5=9,
当且仅当x+1= ,即x=1(x=-3舍去)时,等号成立.
∴当x=1时,函数y= (x>-1)取得最小值9.
3.( )若x>1,求函数y=x+ + 的最小值.
思路点拨:
思路一:将 变形为 ,然后把x+ 看作一个整体进行求解.
思路二:当涉及分数时,通分是最容易想到的常规方法,通分后x+ = ,利用均
值不等式即可求解.
解析 解法一:y=x+ + =x+ + ,令u=x+ ,则u>2,所以y=u+ ≥8,当且仅
当u= ,即u=4时,此时x=2+ ,等号成立.
解法二:y=x+ + = + ≥2 =8,当且仅当 = ,即x=
2+ 时,等号成立.
4.( )已知a>b>0,求a2+ 的最小值.
思路点拨:
分析目标式的特点,对目标式进行适当变形,然后利用均值不等式求最小值.
解析 解法一:由于a2+ 中有两个字母,并注意到b+(a-b)=a,则b(a-b)≤
= ,这样就消去了字母b,因此a2+ ≥a2+ ≥4,当且仅当b=a-b,a
2= ,即a= ,b= 时,等号成立.故a2+ 的最小值为4.
解法二:注意到b+(a-b)=a,则[b+(a-b)]2=a2,则a2+ =[b+(a-b)]2+ ≥4b(a-
b)+ ≥4,当且仅当b=a-b,4b(a-b)= ,即a= ,b= 时,等号成立.故a2+
的最小值为4.
已知x>0,y>0,且 + =1.
问题
1.怎样求x+y的最小值
提示:消元法或利用均值不等式求解.
2.若将已知条件改为xy≠0,且 + =1,怎样求x+y的最小值
提示:先消元,再利用均值不等式求解.
利用均值不等式解决条件求值问题
求含有条件的最大(小)值的基本方法
1.代入消去一个变量,化为求只含一个变量的代数式的最大(小)值问题,解题时要
注意将消去变量的取值范围转化到保留的变量中.
2.分析条件与结论的关系,利用关系解题,这种方法运算量小但技巧性强,平时要多总结.例如:
常数代换:这种方法常用于“已知ax+by=m(a,b,x,y均为正数),求 + 的最小值”
和“已知 + =1(a,b,x,y均为正数),求x+y的最小值”两种类型.
破疑典例
1.( )已知a>0,b>0,若不等式 + ≥ 恒成立,则m的最大值为 ( )
A.9 B.12 C.18 D.24
思路点拨:
先将不等式变形,再利用均值不等式求解.
B 因为a>0,b>0,不等式 + ≥ 恒成立,所以m≤ .
因为(a+3b) =6+ + ≥6+2 =12,
当且仅当a=3b时取等号,所以m的最大值为12.故选B.
2.( )(1)已知a,b,x,y均为正数,且 + =1,求x+y的最小值;
(2)已知x>0,y>0,且x+2y+xy=30,求xy的最大值.
思路点拨:
问题(1)既可以采用常数代换的方法,也可以进行变量代换,再利用均值不等式求
解;问题(2)既可以利用均值不等式求解,也可以采用变量代换的方法求解.
解析 (1)解法一:x+y=(x+y)· =a+b+ + ≥a+b+2 ,当且仅当
即 时,等号成立,故x+y的最小值为a+b+2 .
解法二:由 + =1得x= ,
∴x+y= +y= +y
=a+ +y= +(y-b)+a+b.
∵x>0,y>0,a>0,∴由 >0得y-b>0,∴x+y≥2 +a+b,
当且仅当
即 时,等号成立,故x+y的最小值为a+b+2 .
(2)解法一:由x+2y+xy=30,可得y= (0
=
=34- ,
注意到x+2+ ≥2· =16,可得xy≤18,
当且仅当x+2= ,即x=6时,等号成立,代入x+2y+xy=30中得y=3,故xy的最大值为
18.
解法二:∵x,y>0,∴x+2y≥2 =2 · ,
∴2 · +xy≤x+2y+xy=30,
解此不等式得0≤xy≤18,即xy的最大值为18,此时 即
3.( )已知x,y,z为正实数且满足x-2y+3z=0,求 的最小值.
思路点拨:
由已知得y= 代入 利用均值不等式求最小值.
解析 由x-2y+3z=0,得y= .因为x,y,z为正实数,所以 = = + +6 ≥ 2 +6 =3,当且仅当x=3z时,等号成立,故 的最小值为3.
