2022年新教材高中数学第二章等式与不等式2.2不等式的解集课件新人教B版必修第一册(共21张PPT)
文档属性
| 名称 | 2022年新教材高中数学第二章等式与不等式2.2不等式的解集课件新人教B版必修第一册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 417.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:57:19 | ||
图片预览








文档简介
(共21张PPT)
2.2.2 不等式的解集
1.会求不等式及不等式组的解集.
2.理解绝对值的概念,会解绝对值不等式.
3.理解并掌握数轴上两点之间的距离公式及中点坐标公式.
不等式的解集与不等式组的解集
1.一元一次不等式的解法
第一步:化为ax>(<)b的形式.
第二步:当a>0时,x>(<)① ;
当a<0时,② x<(>) .
第三步:写出解集.
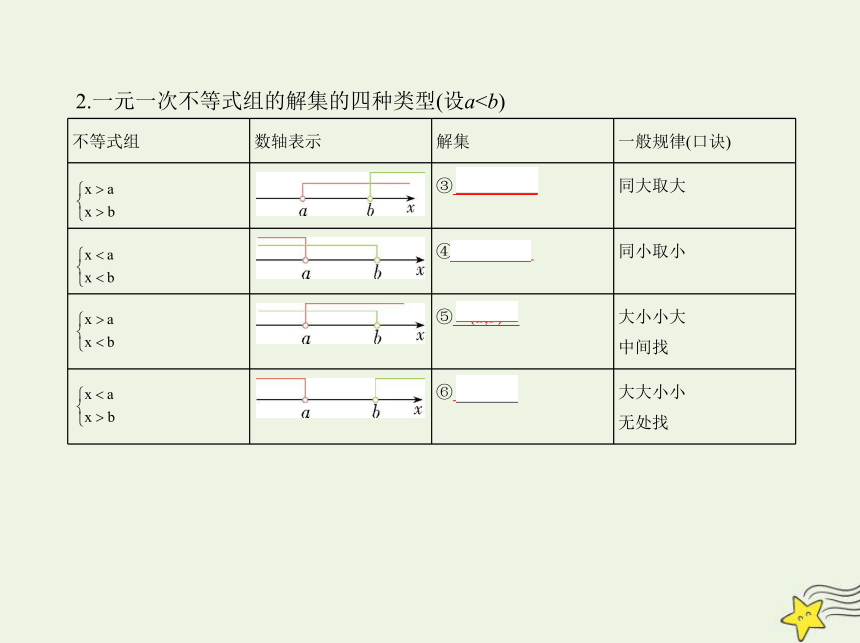
不等式组 数轴表示 解集 一般规律(口诀)
③ (b,+∞) 同大取大
④ (-∞,a) 同小取小
⑤ (a,b) 大小小大
中间找
⑥ 大大小小
无处找
2.一元一次不等式组的解集的四种类型(设a 绝对值不等式
1.一般地,含有绝对值的不等式称为绝对值不等式.
2.绝对值不等式|x|a的解集:
3.|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法:
(1)|ax+b|≤c ⑨ -c≤ax+b≤c .
(2)|ax+b|≥c ⑩ ax+b≥c或ax+b≤-c .
不等式 a>0 a=0 a<0
|x||x|>a ⑧ {x|x>a或x<-a} {x∈R|x≠0} R
数轴上两点之间的距离公式和中点坐标公式
1.一般地,如果实数a,b在数轴上对应的点分别为A,B,即A(a),B(b),则线段AB的长为
AB= |a-b| .
2.如果线段AB的中点M对应的数为x,则x= .
判断正误,正确的画“√”,错误的画“ ”.
1.数轴上两点A(2),B(-1)之间的距离为1.( )
2.数轴上两点A(-2),B(-4)的中点C对应的数为-3. ( √ )
3.不等式2x-4>0的解集为x> . ( )
4.不等式组 的解集是 . ( √ )
5.不等式1<|x+1|<3的解集为(-4,-2)∪(0,2). ( √ )
由1<|x+1|<3,得1∪(0,2).
6.不等式|x|·(1-2x)>0的解集是 .( )
原不等式等价于 解得x< 且x≠0,即x∈(-∞,0)∪ .
某运算程序如图所示,从“输入实数x”到“结果是否小于18”为一次程序操作,
输入x后程序操作仅进行一次就停止了.
不等式的解集与不等式组的解集
问题
1.情景中的运算程序涉及的不等式是什么
提示:根据运算程序,可得不等式3x-6<18.
2.如何求解程序中涉及的不等式
提示:利用不等式的性质.
3.如何求不等式组的解集
提示:分别求出不等式组中每个不等式的解集,然后取交集(可借助数轴).
确定不等式组的解集的两种方法
1.口诀法:求不等式组的解集时,可记住以下规律:同大取大,同小取小,大小小大中
间找,大大小小无处找.
2.数轴法:运用数轴确定不等式组的解集,就是将不等式组中的每一个不等式的解
集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组
的解集,若没有公共部分,则这个不等式组的解集为 .
与不等式(组)相关的参数问题
1.已知含有参数的不等式(组)的解集时,可以先进行化简,表示出不等式(组)的解
集,然后与已知解集进行比较,求出参数的值或取值范围.
2.当一元一次不等式组化简后的解集中含有参数时,可以根据已知条件中解集的
特点,列不等式(组)或列方程(组)来确定参数的值或取值范围.
破疑典例
1.( )已知关于x的不等式组 有3个整数解,则实数a的取值范
围是 ( )
A.-6≤a<-5
B.-6C.-6D.-6≤a≤-5
思路点拨:
解不等式组,可得不等式组的解集,根据不等式组有3个整数解,列出关于a的不等
式求解.
B 由 - x<-1,解得x>4,由4(x-1)≤2(x-a),解得x≤2-a,故不等式组的解集为{x|4
由关于x的不等式组 有3个整数解,得7≤2-a<8,解得-6B.
2.( )求不等式组 (a∈R)的解集.
思路点拨:
先求解不等式1-2x≥3x-4,再分a>0,a=0,a<0三种情况求解不等式ax≥2,其中a>0时
需对 与1的大小再进行讨论,注意分类讨论标准,最后取两个不等式解集的交集.
解析 由1-2x≥3x-4得5x≤5,∴x≤1.
当a=0时,ax≥2化为0×x≥2,无解.∴不等式组的解集为 .
当a>0时,由ax≥2得x≥ . (i)当a=2时,不等式组的解集为{1};
(ii)当a>2时,不等式组的解集为 ;
(iii)当0当a<0时,由ax≥2得x≤ ,不等式组的解集为 .
综上,当a<0时,解集为 ;当0≤a<2时,解集为 ;当a=2时,解集为{1};当a>2
时,解集为 .
问题
1.当c<0时,|ax+b|≤c,|ax+b|≥c的解集分别是什么
提示:c<0时,|ax+b|≤c的解集为 ,|ax+b|≥c的解集为R.
2.如何解含绝对值的不等式
提示:利用绝对值的意义和性质,去绝对值转化为不含绝对值的不等式或不等式
组,再进一步求解.
含绝对值的不等式的解法
1.求解绝对值不等式的关键是去掉绝对值符号,其常用方法有:
(1)定义法;(2)平方法;(3)换元法;(4)数形结合法.
2.含一个绝对值的不等式的常见类型及其解法:
(1)形如|ax+b|c(c∈R)型不等式.
此类不等式的简单解法是利用等价命题求解,即
①当c>0时,|ax+b||ax+b|>c ax+b>c或ax+b<-c.
②当c=0时,|ax+b|c ax+b≠0.
③当c<0时,|ax+b|c ax+b有意义.
(2)形如c<|ax+b|c>0)型不等式.
此类不等式的简单解法是利用等价命题求解,即c<|ax+b|d3.含一个绝对值的其他类型不等式的解法:
(1)形如|ax+b|g(x)型不等式,其中g(x)表示含x的整式.
此类不等式的简单解法是利用等价命题求解,即
①|ax+b|②|ax+b|>g(x) ax+b>g(x)或ax+b<-g(x).
(2)形如|ax+b|ax+b型不等式.
此类不等式的简单解法是利用绝对值的含义去绝对值,即
|ax+b|>ax+b ax+b<0,
|ax+b|4.含两个绝对值的不等式:
(1)形如|f(x)|<|g(x)|型不等式,此类不等式的简单解法是平方法,即
|f(x)|<|g(x)| [f(x)]2<[g(x)]2 [f(x)+g(x)]·[f(x)-g(x)]<0,其中 f(x),g(x)表示含x的整式.
(2)|x1-x2|表示数轴上A(x1)和B(x2)两点间的距离;|x-x1|+|x-x2|表示数轴上点M(x)到A(x
1)和B(x2)两点的距离之和;|x-x1|-|x-x2|表示数轴上点M(x)到A(x1)和B(x2)两点的距离
之差.
解|x+m|+|x+n|>k(二是找准使|x+m|+|x+n|=k的x值.
(3)绝对值不等式“恒成立”问题,往往转化为最值问题求解.
1.( )求下列不等式的解集.
(1)|1-2x|≤3;
(2)1<|x-2|≤3;
(3)|2x+5|>7+x;
思路点拨:
利用绝对值的意义和性质转化为不含绝对值的不等式(组)求解.
解析 (1)原不等式可化为|2x-1|≤3,得-3≤2x-1≤3,从而-2≤2x≤4,得解集为{x|-1
≤x≤2}.
(2)解法一:原不等式等价于不等式组
解得
所以-1≤x<1或3所以原不等式的解集为{x|-1≤x<1或3解法二:原不等式可转化为
①
或②
由①得3所以原不等式的解集是{x|-1≤x<1或3(3)由不等式|2x+5|>7+x,可得2x+5>7+x或2x+5<-(7+x),
解得x>2或x<-4.
所以原不等式的解集是{x|x<-4或x>2}.
(4)∵|x+3|≥0,
∴原不等式等价于|2x-1|-2>0且x≠-3,
即|2x-1|>2,且x≠-3,
∴2x-1>2或2x-1<-2,且x≠-3,
解得x> 或x<- 且x≠-3,
∴原不等式的解集为
.
2.( )解下列不等式:
(1)||x|-4|≤2;
(2)|x-2|+|x+1|>5.
思路点拨:
(1)根据绝对值的意义去绝对值求解;(2)根据绝对值的几何意义,使用数形结合法
求解.
解析 (1)||x|-4|≤2 -2≤|x|-4≤2 2≤|x|≤6 -6≤x≤-
2或2≤x≤6.
故不等式的解集为[-6,-2]∪[2,6].
(2)|x-2|表示数轴上M(x)到A(2)的距离,|x+1|表示数轴上M(x)到B(-1)的距离,如图,
∵AB=3,∴当点M在P或Q,即x=-2或x=3时,|x-2|+|x+1|=5;当点M在P、Q之间时,|x-2|
+|x+1|<5;当点M在线段PQ之外时,|x-2|+|x+1|>5.故不等式的解集为(-∞,-2)∪(3,+∞).
3.( )若不等式|x-3|+|x+3|≥a恒成立,求实数a的取值范围.
思路点拨:
|x-3|+|x+3|≥a恒成立,只要保证a不大于|x-3|+|x+3|的最小值即可.
解析 |x-3|表示数轴上点M(x)到点A(3)的距离,|x+3|表示数轴上点M(x)到点B(-3)
的距离.
∵A、B两点间的距离为|3-(-3)|=6,∴|x-3|+|x+3|表示的M(x)到A、B两点距离之和
的最小值为6,∴a≤6,∴a的取值范围是(-∞,6].
2.2.2 不等式的解集
1.会求不等式及不等式组的解集.
2.理解绝对值的概念,会解绝对值不等式.
3.理解并掌握数轴上两点之间的距离公式及中点坐标公式.
不等式的解集与不等式组的解集
1.一元一次不等式的解法
第一步:化为ax>(<)b的形式.
第二步:当a>0时,x>(<)① ;
当a<0时,② x<(>) .
第三步:写出解集.
不等式组 数轴表示 解集 一般规律(口诀)
③ (b,+∞) 同大取大
④ (-∞,a) 同小取小
⑤ (a,b) 大小小大
中间找
⑥ 大大小小
无处找
2.一元一次不等式组的解集的四种类型(设a
1.一般地,含有绝对值的不等式称为绝对值不等式.
2.绝对值不等式|x|
3.|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法:
(1)|ax+b|≤c ⑨ -c≤ax+b≤c .
(2)|ax+b|≥c ⑩ ax+b≥c或ax+b≤-c .
不等式 a>0 a=0 a<0
|x||x|>a ⑧ {x|x>a或x<-a} {x∈R|x≠0} R
数轴上两点之间的距离公式和中点坐标公式
1.一般地,如果实数a,b在数轴上对应的点分别为A,B,即A(a),B(b),则线段AB的长为
AB= |a-b| .
2.如果线段AB的中点M对应的数为x,则x= .
判断正误,正确的画“√”,错误的画“ ”.
1.数轴上两点A(2),B(-1)之间的距离为1.( )
2.数轴上两点A(-2),B(-4)的中点C对应的数为-3. ( √ )
3.不等式2x-4>0的解集为x> . ( )
4.不等式组 的解集是 . ( √ )
5.不等式1<|x+1|<3的解集为(-4,-2)∪(0,2). ( √ )
由1<|x+1|<3,得1
6.不等式|x|·(1-2x)>0的解集是 .( )
原不等式等价于 解得x< 且x≠0,即x∈(-∞,0)∪ .
某运算程序如图所示,从“输入实数x”到“结果是否小于18”为一次程序操作,
输入x后程序操作仅进行一次就停止了.
不等式的解集与不等式组的解集
问题
1.情景中的运算程序涉及的不等式是什么
提示:根据运算程序,可得不等式3x-6<18.
2.如何求解程序中涉及的不等式
提示:利用不等式的性质.
3.如何求不等式组的解集
提示:分别求出不等式组中每个不等式的解集,然后取交集(可借助数轴).
确定不等式组的解集的两种方法
1.口诀法:求不等式组的解集时,可记住以下规律:同大取大,同小取小,大小小大中
间找,大大小小无处找.
2.数轴法:运用数轴确定不等式组的解集,就是将不等式组中的每一个不等式的解
集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组
的解集,若没有公共部分,则这个不等式组的解集为 .
与不等式(组)相关的参数问题
1.已知含有参数的不等式(组)的解集时,可以先进行化简,表示出不等式(组)的解
集,然后与已知解集进行比较,求出参数的值或取值范围.
2.当一元一次不等式组化简后的解集中含有参数时,可以根据已知条件中解集的
特点,列不等式(组)或列方程(组)来确定参数的值或取值范围.
破疑典例
1.( )已知关于x的不等式组 有3个整数解,则实数a的取值范
围是 ( )
A.-6≤a<-5
B.-6
思路点拨:
解不等式组,可得不等式组的解集,根据不等式组有3个整数解,列出关于a的不等
式求解.
B 由 - x<-1,解得x>4,由4(x-1)≤2(x-a),解得x≤2-a,故不等式组的解集为{x|4
2.( )求不等式组 (a∈R)的解集.
思路点拨:
先求解不等式1-2x≥3x-4,再分a>0,a=0,a<0三种情况求解不等式ax≥2,其中a>0时
需对 与1的大小再进行讨论,注意分类讨论标准,最后取两个不等式解集的交集.
解析 由1-2x≥3x-4得5x≤5,∴x≤1.
当a=0时,ax≥2化为0×x≥2,无解.∴不等式组的解集为 .
当a>0时,由ax≥2得x≥ . (i)当a=2时,不等式组的解集为{1};
(ii)当a>2时,不等式组的解集为 ;
(iii)当0
综上,当a<0时,解集为 ;当0≤a<2时,解集为 ;当a=2时,解集为{1};当a>2
时,解集为 .
问题
1.当c<0时,|ax+b|≤c,|ax+b|≥c的解集分别是什么
提示:c<0时,|ax+b|≤c的解集为 ,|ax+b|≥c的解集为R.
2.如何解含绝对值的不等式
提示:利用绝对值的意义和性质,去绝对值转化为不含绝对值的不等式或不等式
组,再进一步求解.
含绝对值的不等式的解法
1.求解绝对值不等式的关键是去掉绝对值符号,其常用方法有:
(1)定义法;(2)平方法;(3)换元法;(4)数形结合法.
2.含一个绝对值的不等式的常见类型及其解法:
(1)形如|ax+b|
此类不等式的简单解法是利用等价命题求解,即
①当c>0时,|ax+b|
②当c=0时,|ax+b|
③当c<0时,|ax+b|
(2)形如c<|ax+b|
此类不等式的简单解法是利用等价命题求解,即c<|ax+b|
(1)形如|ax+b|
此类不等式的简单解法是利用等价命题求解,即
①|ax+b|
(2)形如|ax+b|
此类不等式的简单解法是利用绝对值的含义去绝对值,即
|ax+b|>ax+b ax+b<0,
|ax+b|
(1)形如|f(x)|<|g(x)|型不等式,此类不等式的简单解法是平方法,即
|f(x)|<|g(x)| [f(x)]2<[g(x)]2 [f(x)+g(x)]·[f(x)-g(x)]<0,其中 f(x),g(x)表示含x的整式.
(2)|x1-x2|表示数轴上A(x1)和B(x2)两点间的距离;|x-x1|+|x-x2|表示数轴上点M(x)到A(x
1)和B(x2)两点的距离之和;|x-x1|-|x-x2|表示数轴上点M(x)到A(x1)和B(x2)两点的距离
之差.
解|x+m|+|x+n|>k(
(3)绝对值不等式“恒成立”问题,往往转化为最值问题求解.
1.( )求下列不等式的解集.
(1)|1-2x|≤3;
(2)1<|x-2|≤3;
(3)|2x+5|>7+x;
思路点拨:
利用绝对值的意义和性质转化为不含绝对值的不等式(组)求解.
解析 (1)原不等式可化为|2x-1|≤3,得-3≤2x-1≤3,从而-2≤2x≤4,得解集为{x|-1
≤x≤2}.
(2)解法一:原不等式等价于不等式组
解得
所以-1≤x<1或3
①
或②
由①得3
解得x>2或x<-4.
所以原不等式的解集是{x|x<-4或x>2}.
(4)∵|x+3|≥0,
∴原不等式等价于|2x-1|-2>0且x≠-3,
即|2x-1|>2,且x≠-3,
∴2x-1>2或2x-1<-2,且x≠-3,
解得x> 或x<- 且x≠-3,
∴原不等式的解集为
.
2.( )解下列不等式:
(1)||x|-4|≤2;
(2)|x-2|+|x+1|>5.
思路点拨:
(1)根据绝对值的意义去绝对值求解;(2)根据绝对值的几何意义,使用数形结合法
求解.
解析 (1)||x|-4|≤2 -2≤|x|-4≤2 2≤|x|≤6 -6≤x≤-
2或2≤x≤6.
故不等式的解集为[-6,-2]∪[2,6].
(2)|x-2|表示数轴上M(x)到A(2)的距离,|x+1|表示数轴上M(x)到B(-1)的距离,如图,
∵AB=3,∴当点M在P或Q,即x=-2或x=3时,|x-2|+|x+1|=5;当点M在P、Q之间时,|x-2|
+|x+1|<5;当点M在线段PQ之外时,|x-2|+|x+1|>5.故不等式的解集为(-∞,-2)∪(3,+∞).
3.( )若不等式|x-3|+|x+3|≥a恒成立,求实数a的取值范围.
思路点拨:
|x-3|+|x+3|≥a恒成立,只要保证a不大于|x-3|+|x+3|的最小值即可.
解析 |x-3|表示数轴上点M(x)到点A(3)的距离,|x+3|表示数轴上点M(x)到点B(-3)
的距离.
∵A、B两点间的距离为|3-(-3)|=6,∴|x-3|+|x+3|表示的M(x)到A、B两点距离之和
的最小值为6,∴a≤6,∴a的取值范围是(-∞,6].
