2022年新教材高中数学第二章等式与不等式1.3方程组的解集课件新人教B版必修第一册(共15张PPT)
文档属性
| 名称 | 2022年新教材高中数学第二章等式与不等式1.3方程组的解集课件新人教B版必修第一册(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
2.1.3 方程组的解集
1.掌握一次方程组的解法.
2.理解方程组在实际问题中的应用.
方程组的解集
一般地,将多个方程联立,就能得到方程组.方程组中,由每个方程的解集得到
的交集称为这个方程组的解集.
求方程组解集的过程要不断应用等式的性质,常用的方法是消元法.
方程组的应用
利用方程组解应用题的步骤:审、设、列、解、验、答.
判断正误,正确的画“√”,错误的画“ ”.
1.二元一次方程组的解 用集合可表示为{(1,1)}. ( √ )
2.方程组的解集一定是有限集. ( )
3.当方程组中未知数的个数大于方程的个数时,方程组的解集可能含有无穷多个
元素. ( √ )
4.方程组 的解集可以写成{(x,y,z)|x=z+3,y=2z+2,z∈R}也可以写成
或{(x,y,z)|y=2x-4,z=x-3,x∈R}. ( √ )
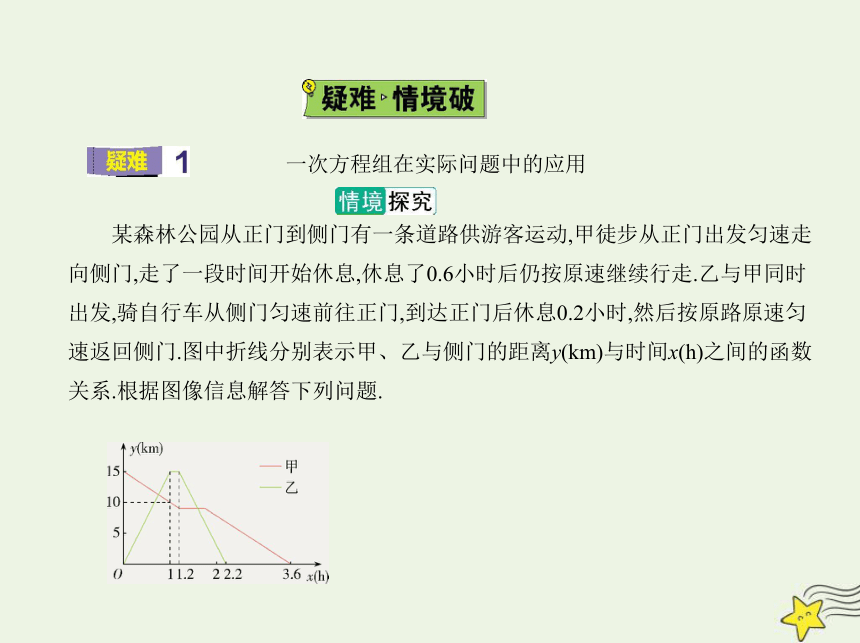
某森林公园从正门到侧门有一条道路供游客运动,甲徒步从正门出发匀速走
向侧门,走了一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时
出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀
速返回侧门.图中折线分别表示甲、乙与侧门的距离y(km)与时间x(h)之间的函数
关系.根据图像信息解答下列问题.
一次方程组在实际问题中的应用
问题
1.求甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式.
提示:设甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式为y=kx+b(k
≠0),0≤x≤1.2,∵点(0,15)和点(1,10)在此函数的图像上,∴ 解得k=-5,b=
15.∴y=-5x+15(0≤x≤1.2).
∴甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式为y=-5x+15(0≤x
≤1.2).
2.甲、乙出发多长时间第一次相遇
提示:设乙骑自行车从侧门匀速前往正门对应的函数关系式为y=mx(m≠0),0≤x
≤1,将(1,15)代入可得m=15,∴乙骑自行车从侧门匀速前往正门对应的函数关系
式为y=15x(0≤x≤1),
∴ 解得x=0.75.
∴甲、乙出发0.75 h第一次相遇.
3.乙回到侧门时,甲与侧门的距离是多少
提示:设甲休息了0.6小时后仍按原速继续行走对应的函数关系式为y=nx+c(n≠
0),1.8≤x≤3.6.
将x=1.2代入y=-5x+15(0≤x≤1.2)中,得y=9.
∴点(1.8,9),(3.6,0)在y=nx+c(n≠0),1.8≤x≤3.6的图像上,
∴ 解得n=-5,c=18.∴y=-5x+18(1.8≤x≤3.6).
将x=2.2代入y=-5x+18(1.8≤x≤3.6),得y=7.
∴乙回到侧门时,甲与侧门的距离是7 km.
(1)找等量关系:认真阅读题目,弄清楚题意,明确问题中的已知量和未知量,找出等
量关系;
(2)设未知数:用字母表示未知数,并用代数式表示其他一些量;
(3)列方程组:根据题目中的相等关系,列出方程组;
(4)解方程组:求出未知数的值;
(5)检验:检验所得的未知数是否合理;
(6)写出答案.
列一次方程组解应用题的一般步骤
破疑典例
1.( )某服装厂专门安排210名工人进行衬衣的手工缝制,每件衬衣由2个衣
袖、1个衣身、1个衣领组成.如果每人每天能够缝制衣袖10个,或衣身15个,或衣
领12个,那么应该安排多少名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、
衣领正好配套
思路点拨:
设应该安排x名工人缝制衣袖,y名工人缝制衣身,z名工人缝制衣领,根据条件列出
关系式求解.
解析 设应该安排x名工人缝制衣袖,y名工人缝制衣身,z名工人缝制衣领,才能使
每天缝制出的衣袖、衣身、衣领正好配套,
依题意有
解得
故应该安排120名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配
套.
2.( )炎夏,有一群孩子在池中游泳,若每个男孩看到其他的人中男孩和女孩
一样多,而每个女孩看到其他的人中男孩比女孩多一倍,求池中男、女孩各多少
人
思路点拨:
设男孩有x个,女孩有y个,列方程组求解.
解析 设男孩有x个,女孩有y个,由题意得
解得 故池中有男孩4个,女孩3个.
方法指导 对于一次方程组的应用问题,解题的关键是先弄懂题意,找出所求问
题需要的条件,列出满足要求的方程组求解.
解方程组
解:设a-1=x,b+2=y,原方程组可变为
解方程组得 即 所以
此种解方程组的方法叫换元法.
方程组的综合应用
问题
如何运用上述方法解下面的方程组
提示:把 -1, +2分别看成一个整体进行换元,将所求方程组进行转换求解,继而
求出a和b的值.
整体换元是解复杂方程组的便捷方法,在数学运算中实施整体换元的关键是发现
或拆分出换元的整体,实施主元替换,整体变形.
解决方程组综合问题的主要流程
方程组解集中的元素是方程组的解,这一关系是求解含参方程组解集问题的依据
和突破口.
破疑典例
1.( )已知集合A={(x,y)|mx+y=5},B={(x,y)|2x-ny=13},小明和小华同时进行A
∩B的运算时,小明看错了m,解得 ,小华看错了n,解得{(3,-7)},你能正确求
解A∩B吗
解析 把 代入2x-ny=13,得7+2n=13,解得n=3;
把(3,-7)代入mx+y=5,得3m-7=5,解得m=4.
所以有
解得
所以A∩B={(2,-3)}.
2.( )已知集合A={(x,y)|ax+y-2=0},B={(x,y)|x-y=0},C={(x,y)|bx-y-1=0},且A∩B
=B∩C={(c,1)},求实数a,b,c的值.
思路点拨:
由{(c,1)}是方程组 的解集,也是 的解集,求出a,b,c的值.
解析 由A∩B={(c,1)},
得 ∴
∴B∩C={(1,1)},
∴b×1-1-1=0,∴b=2.
方法指导 所谓方程组的解,是指该数值满足方程组中的每一个方程.解答此题
的关键是熟知一组方程有公共解集的含义.
2.1.3 方程组的解集
1.掌握一次方程组的解法.
2.理解方程组在实际问题中的应用.
方程组的解集
一般地,将多个方程联立,就能得到方程组.方程组中,由每个方程的解集得到
的交集称为这个方程组的解集.
求方程组解集的过程要不断应用等式的性质,常用的方法是消元法.
方程组的应用
利用方程组解应用题的步骤:审、设、列、解、验、答.
判断正误,正确的画“√”,错误的画“ ”.
1.二元一次方程组的解 用集合可表示为{(1,1)}. ( √ )
2.方程组的解集一定是有限集. ( )
3.当方程组中未知数的个数大于方程的个数时,方程组的解集可能含有无穷多个
元素. ( √ )
4.方程组 的解集可以写成{(x,y,z)|x=z+3,y=2z+2,z∈R}也可以写成
或{(x,y,z)|y=2x-4,z=x-3,x∈R}. ( √ )
某森林公园从正门到侧门有一条道路供游客运动,甲徒步从正门出发匀速走
向侧门,走了一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时
出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀
速返回侧门.图中折线分别表示甲、乙与侧门的距离y(km)与时间x(h)之间的函数
关系.根据图像信息解答下列问题.
一次方程组在实际问题中的应用
问题
1.求甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式.
提示:设甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式为y=kx+b(k
≠0),0≤x≤1.2,∵点(0,15)和点(1,10)在此函数的图像上,∴ 解得k=-5,b=
15.∴y=-5x+15(0≤x≤1.2).
∴甲在休息前与侧门的距离y(km)与时间x(h)之间的函数关系式为y=-5x+15(0≤x
≤1.2).
2.甲、乙出发多长时间第一次相遇
提示:设乙骑自行车从侧门匀速前往正门对应的函数关系式为y=mx(m≠0),0≤x
≤1,将(1,15)代入可得m=15,∴乙骑自行车从侧门匀速前往正门对应的函数关系
式为y=15x(0≤x≤1),
∴ 解得x=0.75.
∴甲、乙出发0.75 h第一次相遇.
3.乙回到侧门时,甲与侧门的距离是多少
提示:设甲休息了0.6小时后仍按原速继续行走对应的函数关系式为y=nx+c(n≠
0),1.8≤x≤3.6.
将x=1.2代入y=-5x+15(0≤x≤1.2)中,得y=9.
∴点(1.8,9),(3.6,0)在y=nx+c(n≠0),1.8≤x≤3.6的图像上,
∴ 解得n=-5,c=18.∴y=-5x+18(1.8≤x≤3.6).
将x=2.2代入y=-5x+18(1.8≤x≤3.6),得y=7.
∴乙回到侧门时,甲与侧门的距离是7 km.
(1)找等量关系:认真阅读题目,弄清楚题意,明确问题中的已知量和未知量,找出等
量关系;
(2)设未知数:用字母表示未知数,并用代数式表示其他一些量;
(3)列方程组:根据题目中的相等关系,列出方程组;
(4)解方程组:求出未知数的值;
(5)检验:检验所得的未知数是否合理;
(6)写出答案.
列一次方程组解应用题的一般步骤
破疑典例
1.( )某服装厂专门安排210名工人进行衬衣的手工缝制,每件衬衣由2个衣
袖、1个衣身、1个衣领组成.如果每人每天能够缝制衣袖10个,或衣身15个,或衣
领12个,那么应该安排多少名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、
衣领正好配套
思路点拨:
设应该安排x名工人缝制衣袖,y名工人缝制衣身,z名工人缝制衣领,根据条件列出
关系式求解.
解析 设应该安排x名工人缝制衣袖,y名工人缝制衣身,z名工人缝制衣领,才能使
每天缝制出的衣袖、衣身、衣领正好配套,
依题意有
解得
故应该安排120名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配
套.
2.( )炎夏,有一群孩子在池中游泳,若每个男孩看到其他的人中男孩和女孩
一样多,而每个女孩看到其他的人中男孩比女孩多一倍,求池中男、女孩各多少
人
思路点拨:
设男孩有x个,女孩有y个,列方程组求解.
解析 设男孩有x个,女孩有y个,由题意得
解得 故池中有男孩4个,女孩3个.
方法指导 对于一次方程组的应用问题,解题的关键是先弄懂题意,找出所求问
题需要的条件,列出满足要求的方程组求解.
解方程组
解:设a-1=x,b+2=y,原方程组可变为
解方程组得 即 所以
此种解方程组的方法叫换元法.
方程组的综合应用
问题
如何运用上述方法解下面的方程组
提示:把 -1, +2分别看成一个整体进行换元,将所求方程组进行转换求解,继而
求出a和b的值.
整体换元是解复杂方程组的便捷方法,在数学运算中实施整体换元的关键是发现
或拆分出换元的整体,实施主元替换,整体变形.
解决方程组综合问题的主要流程
方程组解集中的元素是方程组的解,这一关系是求解含参方程组解集问题的依据
和突破口.
破疑典例
1.( )已知集合A={(x,y)|mx+y=5},B={(x,y)|2x-ny=13},小明和小华同时进行A
∩B的运算时,小明看错了m,解得 ,小华看错了n,解得{(3,-7)},你能正确求
解A∩B吗
解析 把 代入2x-ny=13,得7+2n=13,解得n=3;
把(3,-7)代入mx+y=5,得3m-7=5,解得m=4.
所以有
解得
所以A∩B={(2,-3)}.
2.( )已知集合A={(x,y)|ax+y-2=0},B={(x,y)|x-y=0},C={(x,y)|bx-y-1=0},且A∩B
=B∩C={(c,1)},求实数a,b,c的值.
思路点拨:
由{(c,1)}是方程组 的解集,也是 的解集,求出a,b,c的值.
解析 由A∩B={(c,1)},
得 ∴
∴B∩C={(1,1)},
∴b×1-1-1=0,∴b=2.
方法指导 所谓方程组的解,是指该数值满足方程组中的每一个方程.解答此题
的关键是熟知一组方程有公共解集的含义.
