高一数学《圆的标准方程》课件

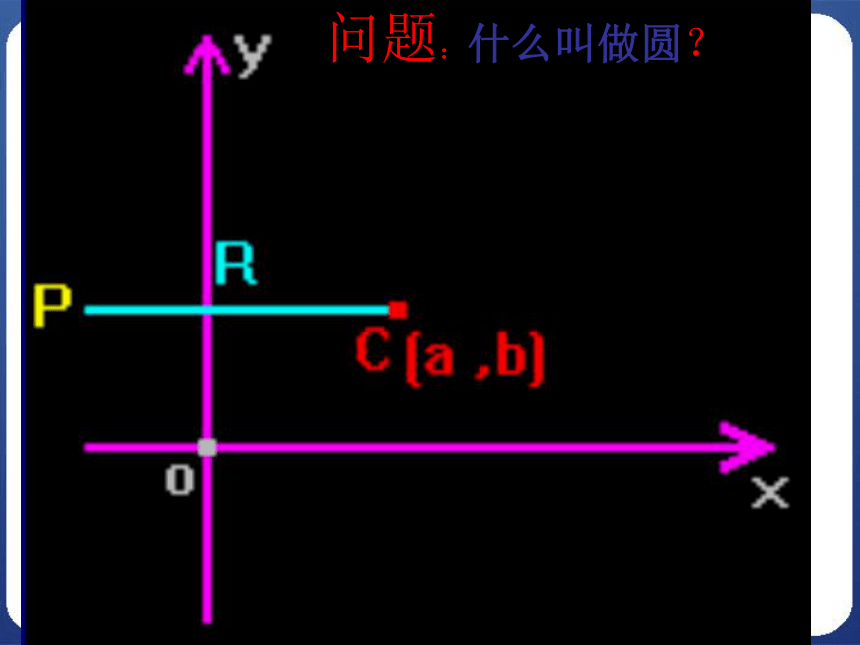
课件18张PPT。4.4.1圆的标准方程问题：什么叫做圆？ 根据圆的定义怎样求出圆心是C(a,b)，
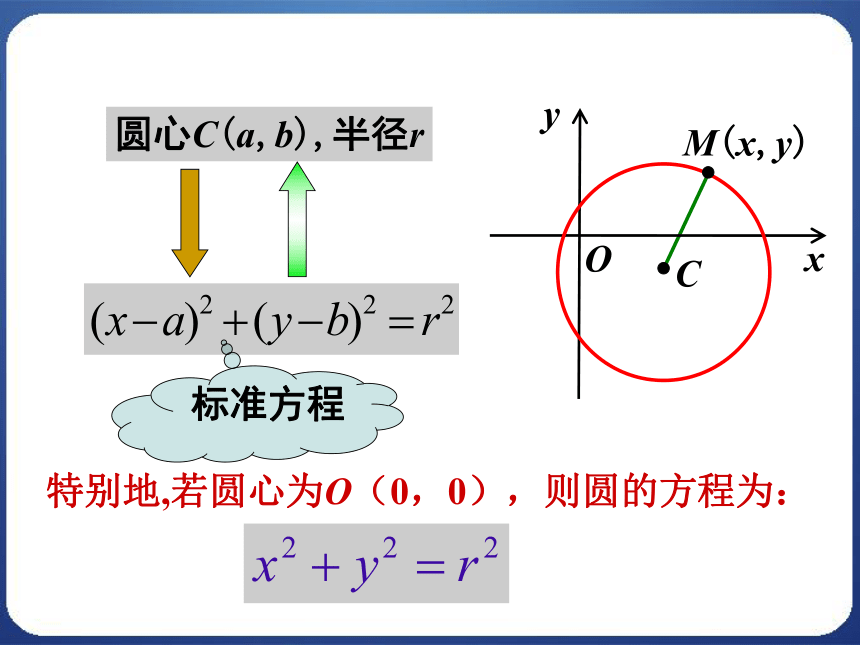
半径是r的圆的方程? 平面内与定点距离等于定长的点的集合(轨迹)是圆,定点就是圆心,定长就是半径.圆的定义 圆心是C(a,b),半径是r,求圆的方程.xyOCM(x,y)设点M (x,y)为圆C上任一点，|MC|= r则P = { M | |MC| = r }圆上所有点的集合(x-a)2+(y-b)2=r2三个独立条件a、b、r确定一个圆的方程.xyOCM(x,y)圆心C(a,b),半径r特别地,若圆心为O（0，0），则圆的方程为：标准方程
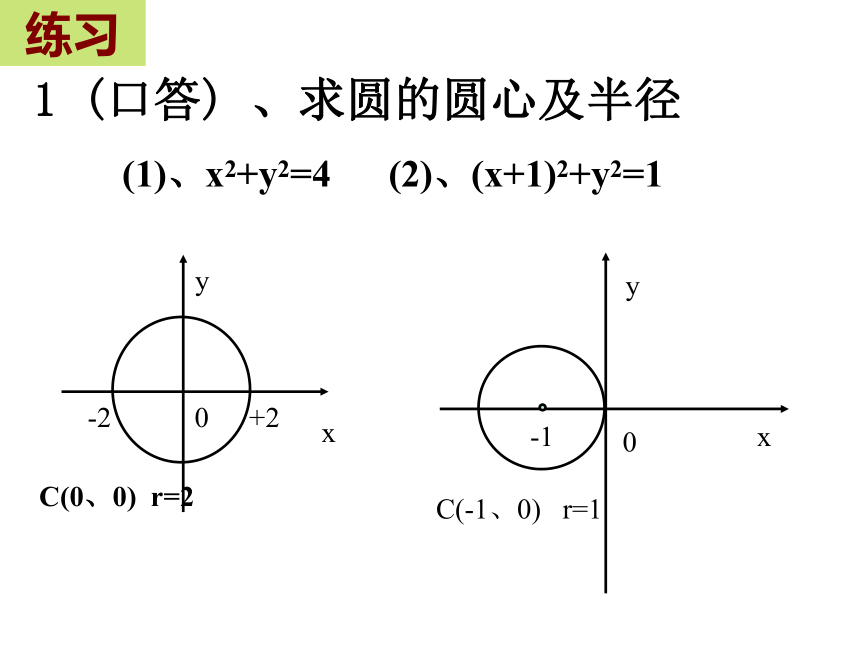
1 (口答) 、求圆的圆心及半径(1)、x2+y2=4 (2)、(x+1)2+y2=1练习
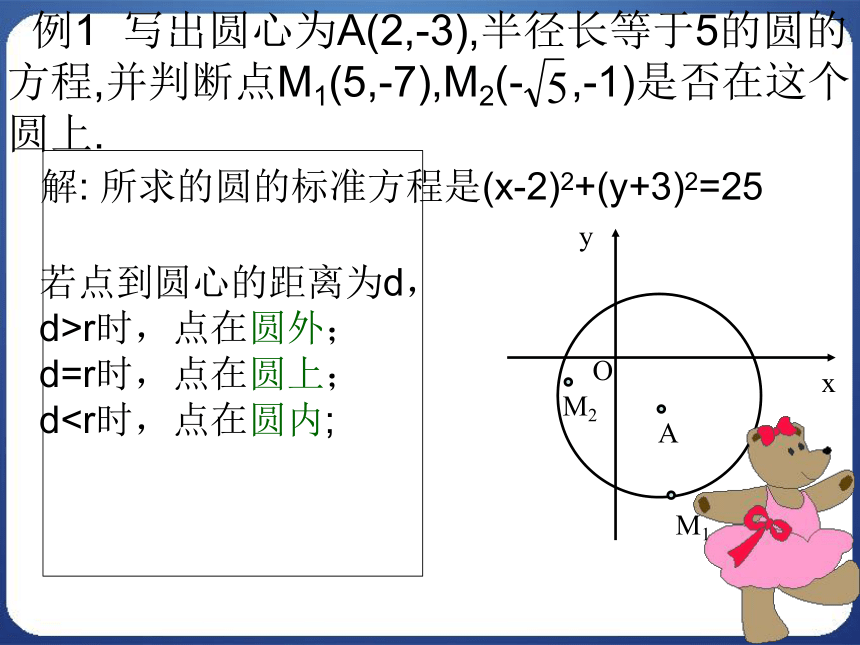
例1 写出圆心为A(2,-3),半径长等于5的圆的
方程,并判断点M1(5,-7),M2(- ,-1)是否在这个
圆上.AxyO解: 所求的圆的标准方程是(x-2)2+(y+3)2=25若点到圆心的距离为d，
d>r时，点在圆外；
d=r时，点在圆上；
d待定系数法解：设所求圆的方程为：因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为 例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程.圆心：两条直线的交点半径：圆心到圆上一点xyOCA(1,1)B(2,-2)弦AB的垂直平分线例3.己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程. 4、求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆.
圆心：已知半径：圆心到切线的距离解：设所求圆的半径为r则：=∴所求圆的方程为：yxOM练习小结圆心C(a,b),半径rxyOCABC1.圆的标准方程2.圆心①两条直线的交点
（弦的垂直平分线）②直径的中点3.半径①圆心到圆上一点②圆心到切线的距离 1)当经过点 的切线的斜率存在时，设所求切线方程为即由得此时切线方程为： 2) 当过点 的切线斜率不存在时，综上所述，所求切线方程为： 或解:结合图形可知 也是切线方程．课堂小结1、圆的标准方程：回顾：求过定点的切线方程的基本方法：
（1）点在圆上 —— 一解；
（2）点不在圆上 —— 两解
特别注意斜率不存在的直线,不要漏解1、求圆心C在直线 x+2y+4=0 上，且过两定点A(-1 , 1)、B(1,-1)的圆的方程。
2、从圆x2+y2=9外一点P(3,2)向该圆引切线，求切线方程。 x=3和5x+12y-39=0例2．已知圆的方程是 ，求经过圆上一点
的切线的方程．解：设切线的斜率为 ,半径 的斜率为由题意： 经过点M的切线方程是即又所求切线方程为即 当M在坐标轴上时，切线方程为：可以看出上面方程同样适用。．或 设 是切线上的任意一点，根据勾股定理，得所以由于把方程整理可得解法二即设 是切线上的任意一点，则 即所求切线方程为解法三1、求圆心C在直线 x+2y+4=0 上，且过两定点A(-1 , 1)、B(1,-1)的圆的方程。
2、从圆x2+y2=9外一点P(3,2)向该圆引切线，求切线方程。 课后思考题：x=3和5x+12y-39=0回顾：求过定点的切线方程的基本方法：
（1）点在圆上 —— 一解；
（2）点不在圆上 —— 两解
特别注意斜率不存在的直线,不要漏解