人教版数学七年级上册 4.1 几何图形 练习(word版含解析)
文档属性
| 名称 | 人教版数学七年级上册 4.1 几何图形 练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 13:32:27 | ||
图片预览

文档简介
人教版数学七年级上册《4.1 几何图形》练习
一 、单选题(本大题共15小题,共45分)
1.如图是一个正方体的展开图,则“心”字对面的字是
A. 核 B. 数 C. 素 D. 学
2.下列图形中不是立体图形的是
A. 圆锥 B. 圆柱 C. 长方形 D. 棱柱
3.如图所示是一个生日蛋糕盒,它的棱的条数是
A. 条 B. 条 C. 条 D. 条
4.下面图形是棱锥的是
A. B. C. D.
5.如图所示的几何体的面数、面与面相交形成的线数、线与线相交形成的点数分别是
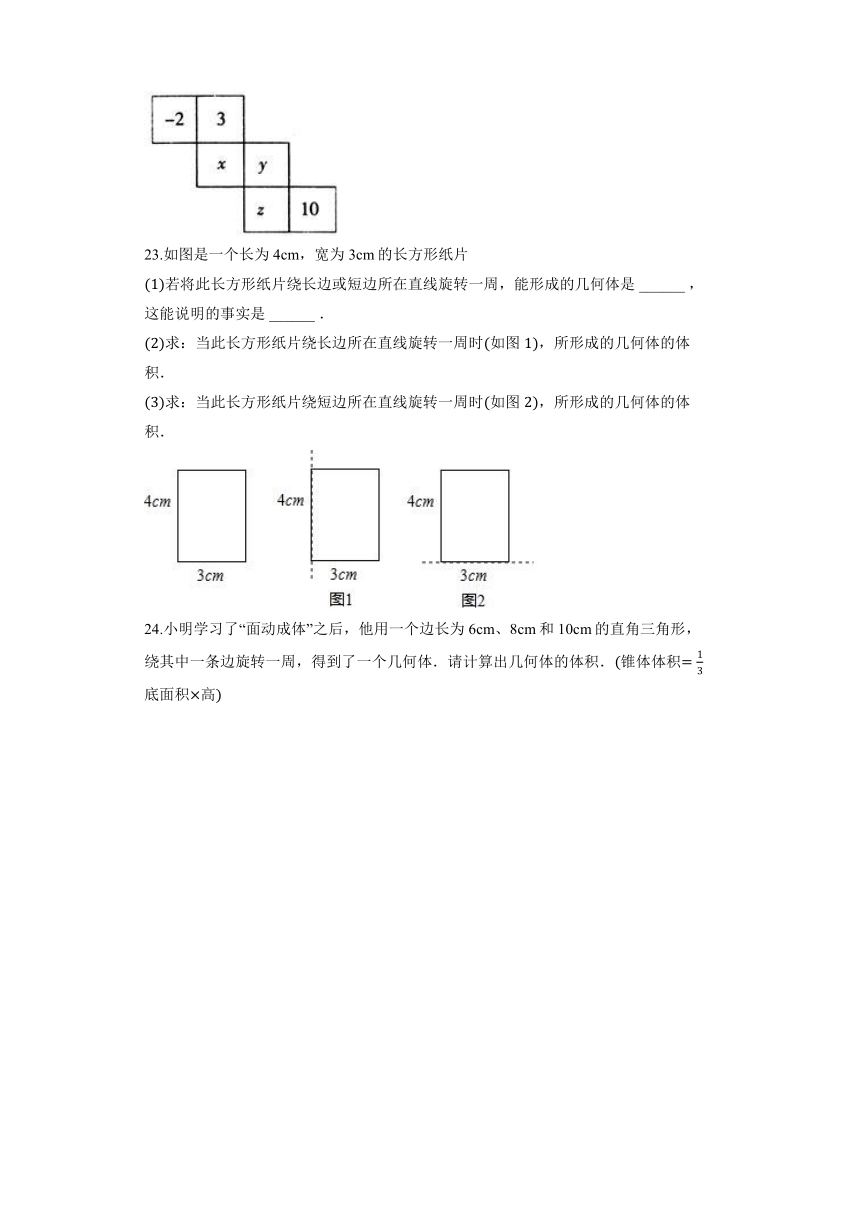
A. ,, B. ,, C. ,, D. ,,
6.下列图形属于棱柱的有
A. 个 B. 个 C. 个 D. 个
7.如图所示的纸板上个无阴影的正方形,从中选择一个,使其与图中个有阴影的正方形一起可以折成一个正方体的包装盒,不同的选法有
A. 种 B. 种 C. 种 D. 种
8.以直角三角形一直角边为轴旋转一周成
A. 圆柱 B. 三棱锥 C. 圆锥 D. 以上都不对
9.下列现象说明“点动成线”的是
A. 汽车雨刷在挡风玻璃上面画出的痕迹
B. 扔一块小石子,石子在空中飞行的路线
C. 旋转一扇门,门在空中运动的痕迹
D. 电风扇通电后它的扇叶旋转,在空中形成的图形
10.将如图所示的平面图形绕直线旋转一周,可以得到的立体图形是
A. B. C. D.
11.已知矩形两边长为与,绕长边旋转一周所得几何体的体积为
A. B. C. D.
12.如图所示绕直线旋转一周所形成的几何体是
A. B. C. D.
13.下面现象能说明“面动成体”的是
A. 旋转一扇门,门运动的痕迹 B. 扔一块小石子,小石子在空中飞行的路线
C. 天空划过一道流星 D. 时钟秒针旋转时扫过的痕迹
14.如图所示的立体图形可以看作直角三角形
A. 绕旋转一周得到 B. 绕旋转一周得到
C. 绕旋转一周得到 D. 绕旋转一周得到
15.如图,从到有①,②,③三条路线,最短的路线是①,其理由是
A. 因为它最直 B. 两点确定一条直线
C. 两点间的距离的概念 D. 两点之间,线段最短
二 、填空题(本大题共5小题,共15分)
16.如图为正方体的一种平面展开图,各面都标有数字,则数字为的面的相对面上的数字是 ______.
17.若一个直棱柱有个顶点,且所有侧棱长的和为,则每条侧棱长为 ______
18.把笔尖看成一个点,用笔在纸上写字的过程揭示了“______”的数学现象.
19.如图,一个长方形边长,绕轴旋转一周得到的立体图形的体积是______结果保留.
20.如图,正方形的边长为,以直线为轴,将正方形旋转一周,所得几何体的主视图的面积是 ______ .
三 、解答题(本大题共4小题,共32分)
21.计算下面圆锥的体积.
22.如图所示的是一个正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数互为相反数,求的绝对值.
23.如图是一个长为,宽为的长方形纸片
若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ______ ,这能说明的事实是 ______ .
求:当此长方形纸片绕长边所在直线旋转一周时如图,所形成的几何体的体积.
求:当此长方形纸片绕短边所在直线旋转一周时如图,所形成的几何体的体积.
24.小明学习了“面动成体”之后,他用一个边长为、和的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.锥体体积底面积高
答案和解析
1.【答案】D;
【解析】解:根据正方体展开图的特征“相间、端是对面”可知,
“心”的对面是“学”,
故选:
根据正方体的展开图的特征进行判断即可.
此题主要考查正方体的展开图的特征,掌握展开图的特征是正确解答的关键.
2.【答案】C;
【解析】解:圆锥体、圆柱体、棱柱是立体图形,而长方形是平面图形,
故选:
根据立体图形、平面图形的意义进行判断即可.
此题主要考查认识立体图形,掌握立体图形、平面图形的意义是正确判断的前提.
3.【答案】C;
【解析】解:六棱柱的棱的条数为条,
故选:
根据六边形的形体特征进行判断即可.
此题主要考查认识立体图形,掌握六棱柱的形体特征是正确判断的前提.
4.【答案】B;
【解析】解:根据图形可知:是六棱柱,是三棱锥,是球体,是圆柱,
故选:
根据图形可知几何体的名称,即可得出答案.
此题主要考查了认识立体图形,掌握柱体、球体、锥体的特点是解决本题的关键.
5.【答案】B;
【解析】解:如图所示的几何体是五棱锥,
五棱锥由个面,有条棱,有个顶点,
故选:
根据五棱锥的形体特征进行解答即可.
此题主要考查认识立体图形,掌握五棱锥的形体特征是正确判断的关键.
6.【答案】B;
【解析】解:第一、二、六个几何体是棱柱共个,
故选:
根据棱柱的概念、结合图形解得即可.
此题主要考查的是立体图形的认识,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥是解答该题的关键.
7.【答案】C;
【解析】解:如图所示:共四种.
故选:
利用正方体的展开图即可解决问题,共四种.
此题主要考查了正方体的展开图.解答该题的关键是掌握四棱柱的特征及正方体展开图的各种情形.
8.【答案】C;
【解析】解:直角三角形绕它的直角边旋转一周可形成圆锥.
故选:
一个直角三角形围绕一条直角边为对称轴旋转一周,根据面动成体的原理可得答案.
此题主要考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
9.【答案】B;
【解析】解:现象属于“线动成面”,故不符合题意;
B.现象属于“点动成线”,故选项符合题意;
C.现象属于“线动成面”,故选项不符合题意;
D.现象属于“线动成面”,故选项不符合题意.
故选:
应用“点动成线,线动成面,面动成体”的性质进行求解即可得出答案.
此题主要考查了点、线、面、体,熟练掌握点、线、面、体的运动观点的性质进行求解是解决本题的关键.
10.【答案】D;
【解析】
本题属于基础题,主要考查学生是否具有基本的识图能力,以及对点线面体之间关系的理解.
根据直角梯形上下底不同得到旋转一周后上下底面圆的大小也不同,进而得到旋转一周后得到的几何体的形状.
解:题中的图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆,因此得到的立体图形应该是一个圆台.
故选D.
11.【答案】C;
【解析】解:将长方形纸片绕长边所在直线旋转一周,得到的几何体是底面半径为,高为的圆柱体,
所以:体积为:,
故选:
将长方形纸片绕长边所在直线旋转一周,得到的几何体是底面半径为,高为的圆柱体,根据圆柱体的体积底面积高求解即可.
此题主要考查点、线、面、体之间的关系,解答该题的关键是旋转后的几何体的各个部分与长方形的长宽之间的关系.
12.【答案】B;
【解析】
该题考查学生立体图形的空间想象能力及分析问题,解决问题的能力,根据面动成体的原理,直角梯形绕直腰旋转一周为圆台进行解答.
解:本题图形可看作是两个梯形绕直线旋转一周得到的几何体,是上底重合的两个圆台体的组合体.
故选B.
13.【答案】A;
【解析】
该题考查了点、线、面、体,准确认识生活实际中的现象是解答该题的关键.
根据点、线、面、体之间的关系对各选项分析判断后利用排除法求解.
解:、旋转一扇门,门运动的痕迹说明“面动成体”,故本选项正确;
B、扔一块小石子,小石子在空中飞行的路线说明“点动成线”,故本选项错误;
C、天空划过一道流星说明“点动成线”,故本选项错误;
D、时钟秒针旋转时扫过的痕迹说明“线动成面”,故本选项错误.
故选A.
14.【答案】B;
【解析】解:根据绕三角形的斜边旋转一周可得两个三角锥,可得:立体图形是绕旋转一周得到的.
故选B.
根据题意可得立体图形是两个三角锥的组合,由此可得出答案.
该题考查面动成体的知识,难度不大,关键是掌握绕三角形的斜边旋转一周可得两个三角锥.
15.【答案】D;
【解析】试题分析:根据两点之间线段最短解答.
从到有①,②,③三条路线,最短的路线是①,其理由是两点之间,线段最短.
故选D.
16.【答案】6;
【解析】解:根据正方体表面展开图的“相间、端是对面”可知,
“”与“”是对面,
故答案为:
根据正方体表面展开图的特征进行判断即可.
此题主要考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确解答的关键.
17.【答案】7;
【解析】解:由一个直棱柱共有个顶点,得棱柱.
由所有侧棱长的和等于,得每条侧棱的长为,
故答案为:
根据棱柱有个顶点,条侧棱,可得答案.
此题主要考查了认识立体图形,熟记棱柱有个顶点,条侧棱是解题关键.
18.【答案】点动成线;
【解析】解:笔尖是点,点在连续运动时,就会连成线,
这个生活现象揭示了“点动成线”的现象,
故答案为:点动成线.
根据平面内点动成线,线动成面,面动成体的基本原理即可求解.
此题主要考查点、线、面、体的关系,熟练掌握点动成线的原理是解答该题的关键.
19.【答案】12π;
【解析】解:一个长方形绕轴旋转一周得到的立体图形是圆柱.
圆柱的体积,
故答案为:
一个矩形绕着它的一边旋转一周,根据面动成体的原理和圆柱的体积即可解.
这道题主要考查点、线、面、体,圆柱的定义,根据圆柱体的形成可作出判断.
20.【答案】;
【解析】解:直线为轴,将正方形旋转一周可得圆柱体,圆柱的高为,底面直径为,
几何体的主视图是长,宽的矩形,
因此面积为:,
故答案为:.
首先根据题意可得将正方形旋转一周可得圆柱体,圆柱的高为,底面直径为,再找出主视图的形状可得答案.
此题主要考查了点、线、面、体,以及三视图,关键是掌握主视图是从几何体的正面看所得到的图形.
21.【答案】解:圆锥的体积:=(c).;
【解析】
根据圆锥的体积解答即可.
此题主要考查立体图形,关键是根据圆锥的体积解答.
22.【答案】解:这是一个正方体的平面展开图,共有六个面,
其中面“”与面“”相对,面“”与面“”相对,面“”与面“”相对,
相对面上的两个数互为相反数,
,,,
解得,,,
.;
【解析】【试题解析】
该题考查了正方体相对两个面上的文字,属于基础题.
根据题意,求出、、的值,从而得到的绝对值.
23.【答案】圆柱;面动成体;
绕长边旋转得到的圆柱的底面半径为,高为,体积;
绕短边旋转得到的圆柱底面半径为,高为,体积.;
【解析】解:若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
故答案为:圆柱;面动成体.
见答案;
见答案.
矩形旋转一周得到圆柱;
绕长边旋转得到的圆柱的底面半径为,高为,从而计算体积即可;
绕短边转得到的圆柱底面半径为,高为,从而计算体积即可.
该题考查了点、线、面、体的知识.
24.【答案】解:以为轴,得
以为轴体积为,
以为轴,得
以为轴的体积为,
以为轴,得
以为轴的体积为
故几何体的体积为:或或.;
【解析】
根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,可得答案.
该题考查了点线面体,利用三角形旋转是圆锥是解题关键.
一 、单选题(本大题共15小题,共45分)
1.如图是一个正方体的展开图,则“心”字对面的字是
A. 核 B. 数 C. 素 D. 学
2.下列图形中不是立体图形的是
A. 圆锥 B. 圆柱 C. 长方形 D. 棱柱
3.如图所示是一个生日蛋糕盒,它的棱的条数是
A. 条 B. 条 C. 条 D. 条
4.下面图形是棱锥的是
A. B. C. D.
5.如图所示的几何体的面数、面与面相交形成的线数、线与线相交形成的点数分别是
A. ,, B. ,, C. ,, D. ,,
6.下列图形属于棱柱的有
A. 个 B. 个 C. 个 D. 个
7.如图所示的纸板上个无阴影的正方形,从中选择一个,使其与图中个有阴影的正方形一起可以折成一个正方体的包装盒,不同的选法有
A. 种 B. 种 C. 种 D. 种
8.以直角三角形一直角边为轴旋转一周成
A. 圆柱 B. 三棱锥 C. 圆锥 D. 以上都不对
9.下列现象说明“点动成线”的是
A. 汽车雨刷在挡风玻璃上面画出的痕迹
B. 扔一块小石子,石子在空中飞行的路线
C. 旋转一扇门,门在空中运动的痕迹
D. 电风扇通电后它的扇叶旋转,在空中形成的图形
10.将如图所示的平面图形绕直线旋转一周,可以得到的立体图形是
A. B. C. D.
11.已知矩形两边长为与,绕长边旋转一周所得几何体的体积为
A. B. C. D.
12.如图所示绕直线旋转一周所形成的几何体是
A. B. C. D.
13.下面现象能说明“面动成体”的是
A. 旋转一扇门,门运动的痕迹 B. 扔一块小石子,小石子在空中飞行的路线
C. 天空划过一道流星 D. 时钟秒针旋转时扫过的痕迹
14.如图所示的立体图形可以看作直角三角形
A. 绕旋转一周得到 B. 绕旋转一周得到
C. 绕旋转一周得到 D. 绕旋转一周得到
15.如图,从到有①,②,③三条路线,最短的路线是①,其理由是
A. 因为它最直 B. 两点确定一条直线
C. 两点间的距离的概念 D. 两点之间,线段最短
二 、填空题(本大题共5小题,共15分)
16.如图为正方体的一种平面展开图,各面都标有数字,则数字为的面的相对面上的数字是 ______.
17.若一个直棱柱有个顶点,且所有侧棱长的和为,则每条侧棱长为 ______
18.把笔尖看成一个点,用笔在纸上写字的过程揭示了“______”的数学现象.
19.如图,一个长方形边长,绕轴旋转一周得到的立体图形的体积是______结果保留.
20.如图,正方形的边长为,以直线为轴,将正方形旋转一周,所得几何体的主视图的面积是 ______ .
三 、解答题(本大题共4小题,共32分)
21.计算下面圆锥的体积.
22.如图所示的是一个正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数互为相反数,求的绝对值.
23.如图是一个长为,宽为的长方形纸片
若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ______ ,这能说明的事实是 ______ .
求:当此长方形纸片绕长边所在直线旋转一周时如图,所形成的几何体的体积.
求:当此长方形纸片绕短边所在直线旋转一周时如图,所形成的几何体的体积.
24.小明学习了“面动成体”之后,他用一个边长为、和的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.锥体体积底面积高
答案和解析
1.【答案】D;
【解析】解:根据正方体展开图的特征“相间、端是对面”可知,
“心”的对面是“学”,
故选:
根据正方体的展开图的特征进行判断即可.
此题主要考查正方体的展开图的特征,掌握展开图的特征是正确解答的关键.
2.【答案】C;
【解析】解:圆锥体、圆柱体、棱柱是立体图形,而长方形是平面图形,
故选:
根据立体图形、平面图形的意义进行判断即可.
此题主要考查认识立体图形,掌握立体图形、平面图形的意义是正确判断的前提.
3.【答案】C;
【解析】解:六棱柱的棱的条数为条,
故选:
根据六边形的形体特征进行判断即可.
此题主要考查认识立体图形,掌握六棱柱的形体特征是正确判断的前提.
4.【答案】B;
【解析】解:根据图形可知:是六棱柱,是三棱锥,是球体,是圆柱,
故选:
根据图形可知几何体的名称,即可得出答案.
此题主要考查了认识立体图形,掌握柱体、球体、锥体的特点是解决本题的关键.
5.【答案】B;
【解析】解:如图所示的几何体是五棱锥,
五棱锥由个面,有条棱,有个顶点,
故选:
根据五棱锥的形体特征进行解答即可.
此题主要考查认识立体图形,掌握五棱锥的形体特征是正确判断的关键.
6.【答案】B;
【解析】解:第一、二、六个几何体是棱柱共个,
故选:
根据棱柱的概念、结合图形解得即可.
此题主要考查的是立体图形的认识,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥是解答该题的关键.
7.【答案】C;
【解析】解:如图所示:共四种.
故选:
利用正方体的展开图即可解决问题,共四种.
此题主要考查了正方体的展开图.解答该题的关键是掌握四棱柱的特征及正方体展开图的各种情形.
8.【答案】C;
【解析】解:直角三角形绕它的直角边旋转一周可形成圆锥.
故选:
一个直角三角形围绕一条直角边为对称轴旋转一周,根据面动成体的原理可得答案.
此题主要考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
9.【答案】B;
【解析】解:现象属于“线动成面”,故不符合题意;
B.现象属于“点动成线”,故选项符合题意;
C.现象属于“线动成面”,故选项不符合题意;
D.现象属于“线动成面”,故选项不符合题意.
故选:
应用“点动成线,线动成面,面动成体”的性质进行求解即可得出答案.
此题主要考查了点、线、面、体,熟练掌握点、线、面、体的运动观点的性质进行求解是解决本题的关键.
10.【答案】D;
【解析】
本题属于基础题,主要考查学生是否具有基本的识图能力,以及对点线面体之间关系的理解.
根据直角梯形上下底不同得到旋转一周后上下底面圆的大小也不同,进而得到旋转一周后得到的几何体的形状.
解:题中的图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆,因此得到的立体图形应该是一个圆台.
故选D.
11.【答案】C;
【解析】解:将长方形纸片绕长边所在直线旋转一周,得到的几何体是底面半径为,高为的圆柱体,
所以:体积为:,
故选:
将长方形纸片绕长边所在直线旋转一周,得到的几何体是底面半径为,高为的圆柱体,根据圆柱体的体积底面积高求解即可.
此题主要考查点、线、面、体之间的关系,解答该题的关键是旋转后的几何体的各个部分与长方形的长宽之间的关系.
12.【答案】B;
【解析】
该题考查学生立体图形的空间想象能力及分析问题,解决问题的能力,根据面动成体的原理,直角梯形绕直腰旋转一周为圆台进行解答.
解:本题图形可看作是两个梯形绕直线旋转一周得到的几何体,是上底重合的两个圆台体的组合体.
故选B.
13.【答案】A;
【解析】
该题考查了点、线、面、体,准确认识生活实际中的现象是解答该题的关键.
根据点、线、面、体之间的关系对各选项分析判断后利用排除法求解.
解:、旋转一扇门,门运动的痕迹说明“面动成体”,故本选项正确;
B、扔一块小石子,小石子在空中飞行的路线说明“点动成线”,故本选项错误;
C、天空划过一道流星说明“点动成线”,故本选项错误;
D、时钟秒针旋转时扫过的痕迹说明“线动成面”,故本选项错误.
故选A.
14.【答案】B;
【解析】解:根据绕三角形的斜边旋转一周可得两个三角锥,可得:立体图形是绕旋转一周得到的.
故选B.
根据题意可得立体图形是两个三角锥的组合,由此可得出答案.
该题考查面动成体的知识,难度不大,关键是掌握绕三角形的斜边旋转一周可得两个三角锥.
15.【答案】D;
【解析】试题分析:根据两点之间线段最短解答.
从到有①,②,③三条路线,最短的路线是①,其理由是两点之间,线段最短.
故选D.
16.【答案】6;
【解析】解:根据正方体表面展开图的“相间、端是对面”可知,
“”与“”是对面,
故答案为:
根据正方体表面展开图的特征进行判断即可.
此题主要考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确解答的关键.
17.【答案】7;
【解析】解:由一个直棱柱共有个顶点,得棱柱.
由所有侧棱长的和等于,得每条侧棱的长为,
故答案为:
根据棱柱有个顶点,条侧棱,可得答案.
此题主要考查了认识立体图形,熟记棱柱有个顶点,条侧棱是解题关键.
18.【答案】点动成线;
【解析】解:笔尖是点,点在连续运动时,就会连成线,
这个生活现象揭示了“点动成线”的现象,
故答案为:点动成线.
根据平面内点动成线,线动成面,面动成体的基本原理即可求解.
此题主要考查点、线、面、体的关系,熟练掌握点动成线的原理是解答该题的关键.
19.【答案】12π;
【解析】解:一个长方形绕轴旋转一周得到的立体图形是圆柱.
圆柱的体积,
故答案为:
一个矩形绕着它的一边旋转一周,根据面动成体的原理和圆柱的体积即可解.
这道题主要考查点、线、面、体,圆柱的定义,根据圆柱体的形成可作出判断.
20.【答案】;
【解析】解:直线为轴,将正方形旋转一周可得圆柱体,圆柱的高为,底面直径为,
几何体的主视图是长,宽的矩形,
因此面积为:,
故答案为:.
首先根据题意可得将正方形旋转一周可得圆柱体,圆柱的高为,底面直径为,再找出主视图的形状可得答案.
此题主要考查了点、线、面、体,以及三视图,关键是掌握主视图是从几何体的正面看所得到的图形.
21.【答案】解:圆锥的体积:=(c).;
【解析】
根据圆锥的体积解答即可.
此题主要考查立体图形,关键是根据圆锥的体积解答.
22.【答案】解:这是一个正方体的平面展开图,共有六个面,
其中面“”与面“”相对,面“”与面“”相对,面“”与面“”相对,
相对面上的两个数互为相反数,
,,,
解得,,,
.;
【解析】【试题解析】
该题考查了正方体相对两个面上的文字,属于基础题.
根据题意,求出、、的值,从而得到的绝对值.
23.【答案】圆柱;面动成体;
绕长边旋转得到的圆柱的底面半径为,高为,体积;
绕短边旋转得到的圆柱底面半径为,高为,体积.;
【解析】解:若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
故答案为:圆柱;面动成体.
见答案;
见答案.
矩形旋转一周得到圆柱;
绕长边旋转得到的圆柱的底面半径为,高为,从而计算体积即可;
绕短边转得到的圆柱底面半径为,高为,从而计算体积即可.
该题考查了点、线、面、体的知识.
24.【答案】解:以为轴,得
以为轴体积为,
以为轴,得
以为轴的体积为,
以为轴,得
以为轴的体积为
故几何体的体积为:或或.;
【解析】
根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,可得答案.
该题考查了点线面体,利用三角形旋转是圆锥是解题关键.
