人教版数学六年级上册《8.数学广角——数与形》单元测试(含答案)
文档属性
| 名称 | 人教版数学六年级上册《8.数学广角——数与形》单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 11:03:39 | ||
图片预览



文档简介
人教版数学六年级上册《8.数学广角——数与形》单元测试
一 、单选题(本大题共10小题,共50分)
1.笑笑用火柴按照右面的方法摆正方形,按这样的方法摆6个正方形共需要( )根火柴.
A. 19 B. 20 C. 24
2.用小棒摆正方形,照这样摆下去,摆10个正方形是( )根小棒.
A. 24 B. 40 C. 31 D. 41
3.观察下面图形的变化,找出图形变化的规律,然后按照这个规律在空格中画出应画的图形.( )
A. B.
4.如图有大小不同的平行四边形,第1幅图中有1个,第2幅图有3个,第3幅图有5个,第n幅图有( )个平行四边形.
A. 2n+1 B. 2n-1 C. n×n
5.下面各图是由棱长为1厘米的正方体拼成的,根据前三个图形表面积的排列规律,第 五个图形的表面积是( )平方厘米.
A. 20 cm2 B. 22 cm2 C. 24 cm2
6.把边长为1的正方形按如图所示的方式排列,则第n个图形的周长用含n(n为正整数)的式子表示为( )
A. 4n B. 2n-2 C. 2n+2 D. 4n-4
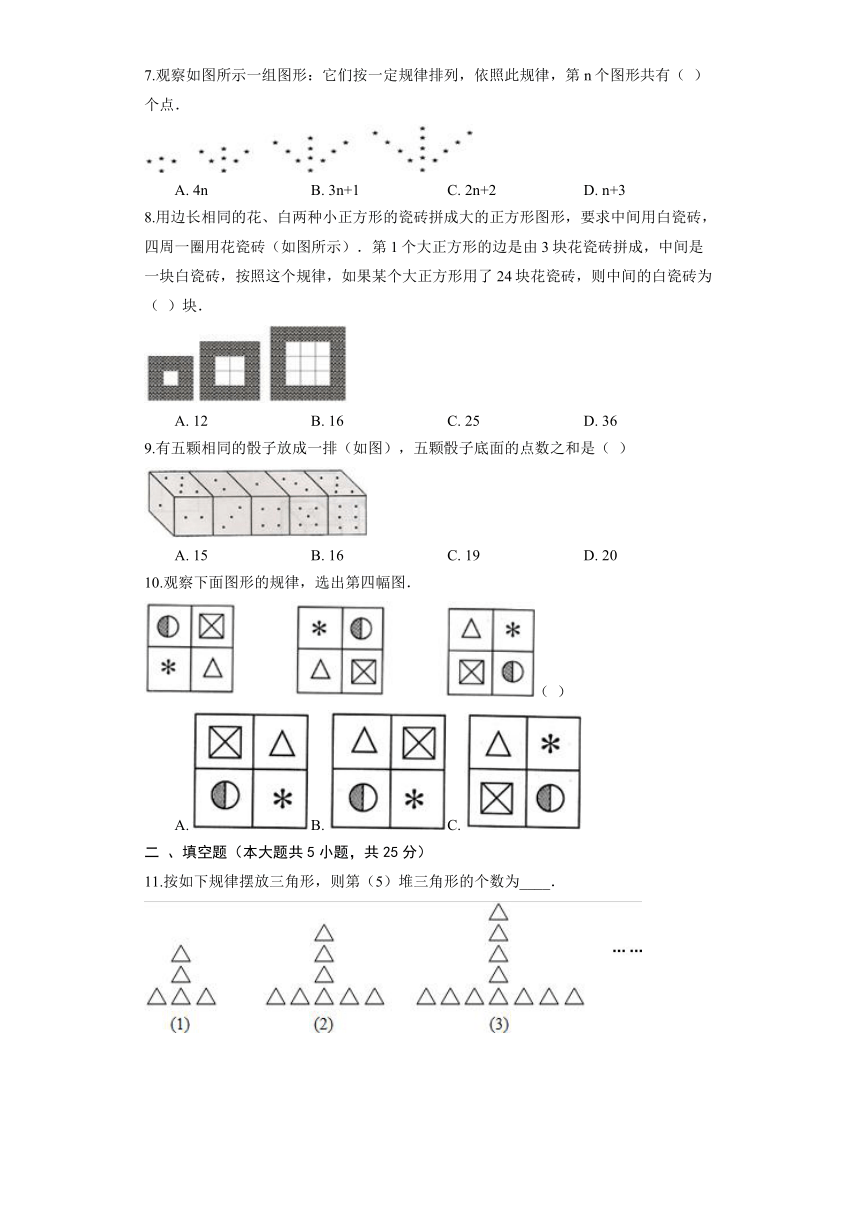
7.观察如图所示一组图形:它们按一定规律排列,依照此规律,第n个图形共有( )个点.
A. 4n B. 3n+1 C. 2n+2 D. n+3
8.用边长相同的花、白两种小正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示).第1个大正方形的边是由3块花瓷砖拼成,中间是一块白瓷砖,按照这个规律,如果某个大正方形用了24块花瓷砖,则中间的白瓷砖为( )块.
A. 12 B. 16 C. 25 D. 36
9.有五颗相同的骰子放成一排(如图),五颗骰子底面的点数之和是( )
A. 15 B. 16 C. 19 D. 20
10.观察下面图形的规律,选出第四幅图.
( )
A. B. C.
二 、填空题(本大题共5小题,共25分)
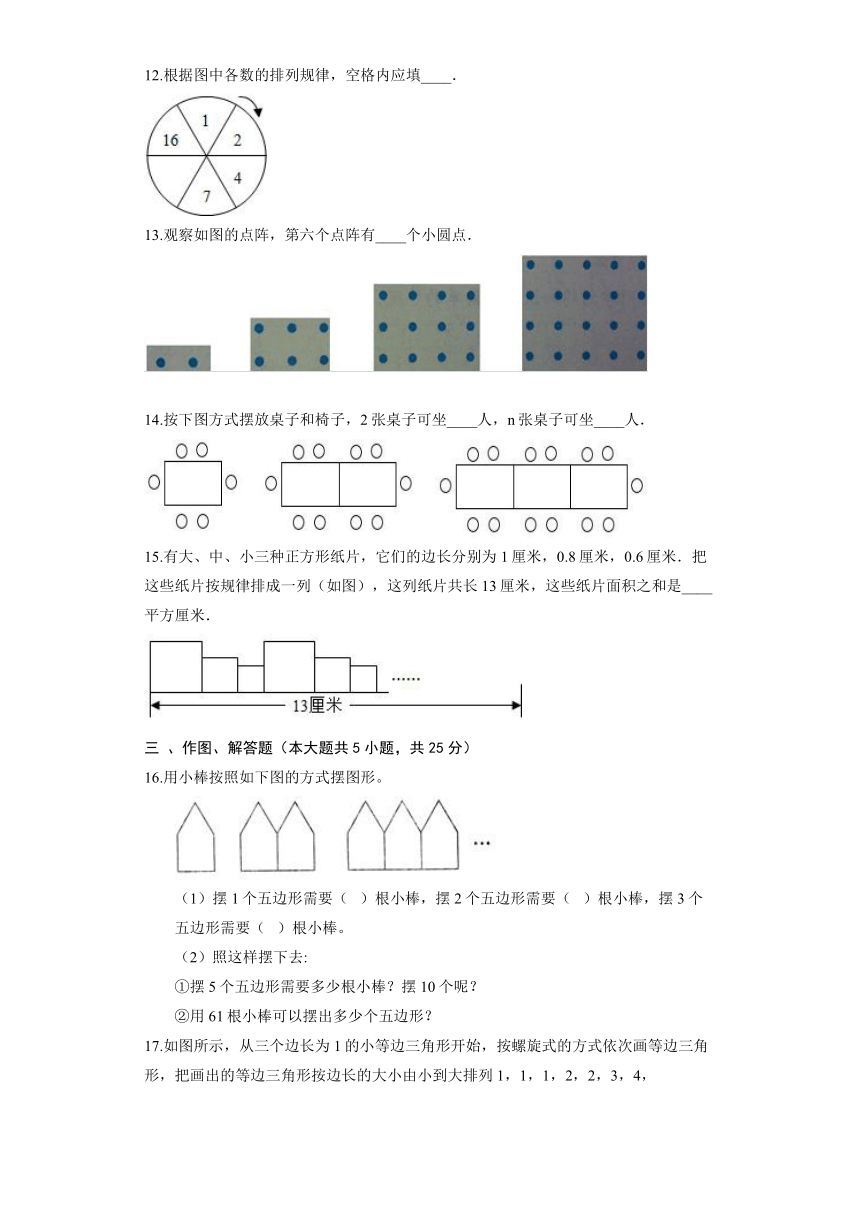
11.按如下规律摆放三角形,则第(5)堆三角形的个数为____.
12.根据图中各数的排列规律,空格内应填____.
13.观察如图的点阵,第六个点阵有____个小圆点.
14.按下图方式摆放桌子和椅子,2张桌子可坐____人,n张桌子可坐____人.
15.有大、中、小三种正方形纸片,它们的边长分别为1厘米,0.8厘米,0.6厘米.把这些纸片按规律排成一列(如图),这列纸片共长13厘米,这些纸片面积之和是____平方厘米.
三 、作图、解答题(本大题共5小题,共25分)
16.用小棒按照如下图的方式摆图形。
(1)摆1个五边形需要( )根小棒,摆2个五边形需要( )根小棒,摆3个五边形需要( )根小棒。
(2)照这样摆下去:
①摆5个五边形需要多少根小棒?摆10个呢?
②用61根小棒可以摆出多少个五边形?
17.如图所示,从三个边长为1的小等边三角形开始,按螺旋式的方式依次画等边三角形,把画出的等边三角形按边长的大小由小到大排列1,1,1,2,2,3,4,5,….请你算出第21个等边三角形的边长是多少?
18.用小棒按照如图的方式摆图形.
(1)摆1个六边形需要____根小棒,摆2个需要____根小棒,摆3个需要____根小棒.
(2)照这样摆下去:
①摆n个六边形需要几根小棒?n是200时,需要几根小棒?
②181根小棒可以摆多少个六边形?
19.用若干相同的小等边三角形,可以拼成大的等边三角形.(如图所示)
(1)填写下面表格,想一想,小三角形的个数与大三角形的层数有什么关系?
(2)如果拼成的大三角形有30层.那么共用了多少个小三角形?
20.根据已知图形填出未知图形.
答案和解析
1.【答案】A;
【解析】解:3×6+1
=18+1
=19(根)
答:按这样的方法摆6个正方形共需要19根火柴.
故选:A.
2.【答案】C;
【解析】解:(10-1)×3+4
=9×3+4
=27+4
=31(根)
答:摆10个同样的正方形需要31根小棒.
故选:C.
3.【答案】B;
【解析】解:图中缺第三个图形,它一共有5个点,横看竖看都有3个点;选项中符合的只有B.
故答案选:B.
4.【答案】B;
【解析】解:第一幅图中有1个
第二幅图中有2×2-1=3(个)
第3幅图中有2×3-1=5(个)
…
可以发现,每个图形都比前一个图形多2个:
所以第n幅图有2n-1个.
故选:B.
5.【答案】B;
【解析】解:(1)1个小正方体,表面积是:6平方厘米可以写成2+1×4;
2个小正方体,表面积是10平方厘米,可以写成2+2×4;
3个小正方体,表面积是14平方厘米,可以写成2+3×4;…;
所以a个小正方体,表面积就是2+4a平方厘米;
当n=5时,表面积是:2+4×5=22(平方厘米),
故选:B.
6.【答案】C;
【解析】解:因为:
n=1时的周长:4=4+0×2
n=2时的周长:7=4+1×2
n=3时的周长:8=4+2×2
…
以此类推第n个的周长为:
4+(n-1)×2=2n+2
故选:C.
7.【答案】B;
【解析】解:观察发现,第1个图形黑点的个数是,1+3=4,
第2个图形黑点的个数是,1+3×2=7,
第3个图形黑点的个数是,1+3×3=10,
第4个图形黑点的个数是,1+3×4=13,
…
依此类推,第n个图形黑点的个数是,1+3×n=3n+1,
故选:B.
8.【答案】C;
【解析】解:(1)填表如下:
大正方形每边的块数每增加1块,所用的花瓷砖块数就增加4块;
(2)大正方形用了24块花瓷砖;
大正方形每边的块数是7,
所以中间的白瓷砖为25
答:白瓷砖用了25块.
故选:C.
9.【答案】C;
【解析】解:根据图示,可得每颗骰子相对的面对应的数是:1对6,2对5,3对4,
所以每颗骰子每个相对的面的两个数字的和是:1+6=2+5=3+4=7;
所以五颗骰子底面的点数之和是:
7×5-(5+2+1+3+5)
=35-16
=19
答:五颗骰子底面的点数之和是19.
故选:C.
10.【答案】A;
【解析】解:根据题干分析可得,第四方图形是
.
故选:A.
11.【答案】17;
【解析】解:第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△.
当n=5时,
3×5+2
=15+2
=17(个).
故答案为:17.
12.【答案】11;
【解析】解:根据题干分析所得规律:7+4=11,
所以空格内应填11.
故答案为:11.
13.【答案】42;
【解析】解:根据题干分析可得每个图中的点数个数的规律是:第n幅图中的点数为:+n;
当n=6时,点阵中的点数为:62+6=42(个);
答:第六个点阵中有42个点.
故答案为:42.
14.【答案】10;4n+2;
【解析】解:观察图形可知,第一张餐桌可以坐6人,第二张餐桌可以坐6+4=10人,…,
第n张餐桌共能坐6+4(n-1)=4n+2人,
答:2张桌子可坐 10人,n张桌子可坐 4n+2人.
故答案为:10;4n+2.
15.【答案】11;
【解析】解:1+0.8+0.6=2.4(厘米),
13÷2.4=5…1(厘米),即共经历了5个周期又多出来1厘米,
所以共有6个大正方形,5个中正方形5个小正方形,
所以这些纸片的面积之和是:
1×1×6+0.8×0.8×5+0.6×0.6×5,
=6+3.2+1.8,
=11(平方厘米);
答:这些纸片的面积之和是11平方厘米.
故答案为:11.
16.【答案】(1)5 9 13
(2)①21根 41根 ②15个;
【解析】略
17.【答案】解:根据题干分析,这组三角形的边长可以继续排列为:
1、1、1、2、2、3、4、5、7、9、12、16、21、28、37、49、65、86、114、151、200;
所以第21个三角形的边长是200.
答:第21个等边三角形的边长是200.;
【解析】观察题干中的数据“1,1,1,2,2,3,4,5,…”可得:第一个三角形的边长加第二个三角形的边长等于第四个三角形的边长,第二个三角形的边长加第三个三角形的边长等于第五个三角形的边长,第三个加第四个等于第六个,…依次排列即可得出第21个三角形的边长,由此即可解答.
18.【答案】解:根据题干分析可得:(1)摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要16根小棒,可以写成:5×3+1;…
(2)①摆n个六边形需要:5n+1根小棒,
当n=200时,需要小棒5×200+1=1001(根);
②当5n+1=181时,可以摆成的六边形有:n=(181-1)÷5=36(个);
答:摆n个六边形需要5n+1根小棒?,是200时,需要1001根小棒,181根小棒可以摆36个六边形;
故答案为:6,11,16.;
【解析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
19.【答案】解:(1)如下表,小三角形的个数是大三角形的层数的平方;
(2)共用了三角形:302=900(个);
答:(1)小三角形的个数是大三角形的层数的平方;(2)共用了900个三角形.;
【解析】(1)层数=2,小等边三角形的个数是1+3=4=22,
层数=3,小等边三角形的个数是1+3+5=9=32,
层数=4,小等边三角形的个数是1+3+5+7=16=42,
层数=5,小等边三角形的个数是1+3+5+7+9=25=52,
层数=6,小等边三角形的个数是1+3+5+7+9+11=36=62,
层数=7,小等边三角形的个数是1+3+5+7+9+11+13=49=72,
层数=8,小等边三角形的个数是1+3+5+7+9+11+13+15=64=82,
(2)如果拼成的大三角形有30层.那么共用了302.
20.【答案】解:
;
【解析】①、(1)中左上角的蓝色正方形1,在(2)中到了右上角,在(3)中到了右下角,每次转了90度,所以在(4)中应到左下角;
②、(1)中左上角的蓝色正方形2,在(2)中右移一个格,在(3)中下移一个格,每次转了90度,所以在(4)中应左移一个格;
③、(1)中在三行四列的蓝色正方形3,在(2)、(3)中每次都向左移动一个格;到(4)中即如图所示.
一 、单选题(本大题共10小题,共50分)
1.笑笑用火柴按照右面的方法摆正方形,按这样的方法摆6个正方形共需要( )根火柴.
A. 19 B. 20 C. 24
2.用小棒摆正方形,照这样摆下去,摆10个正方形是( )根小棒.
A. 24 B. 40 C. 31 D. 41
3.观察下面图形的变化,找出图形变化的规律,然后按照这个规律在空格中画出应画的图形.( )
A. B.
4.如图有大小不同的平行四边形,第1幅图中有1个,第2幅图有3个,第3幅图有5个,第n幅图有( )个平行四边形.
A. 2n+1 B. 2n-1 C. n×n
5.下面各图是由棱长为1厘米的正方体拼成的,根据前三个图形表面积的排列规律,第 五个图形的表面积是( )平方厘米.
A. 20 cm2 B. 22 cm2 C. 24 cm2
6.把边长为1的正方形按如图所示的方式排列,则第n个图形的周长用含n(n为正整数)的式子表示为( )
A. 4n B. 2n-2 C. 2n+2 D. 4n-4
7.观察如图所示一组图形:它们按一定规律排列,依照此规律,第n个图形共有( )个点.
A. 4n B. 3n+1 C. 2n+2 D. n+3
8.用边长相同的花、白两种小正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示).第1个大正方形的边是由3块花瓷砖拼成,中间是一块白瓷砖,按照这个规律,如果某个大正方形用了24块花瓷砖,则中间的白瓷砖为( )块.
A. 12 B. 16 C. 25 D. 36
9.有五颗相同的骰子放成一排(如图),五颗骰子底面的点数之和是( )
A. 15 B. 16 C. 19 D. 20
10.观察下面图形的规律,选出第四幅图.
( )
A. B. C.
二 、填空题(本大题共5小题,共25分)
11.按如下规律摆放三角形,则第(5)堆三角形的个数为____.
12.根据图中各数的排列规律,空格内应填____.
13.观察如图的点阵,第六个点阵有____个小圆点.
14.按下图方式摆放桌子和椅子,2张桌子可坐____人,n张桌子可坐____人.
15.有大、中、小三种正方形纸片,它们的边长分别为1厘米,0.8厘米,0.6厘米.把这些纸片按规律排成一列(如图),这列纸片共长13厘米,这些纸片面积之和是____平方厘米.
三 、作图、解答题(本大题共5小题,共25分)
16.用小棒按照如下图的方式摆图形。
(1)摆1个五边形需要( )根小棒,摆2个五边形需要( )根小棒,摆3个五边形需要( )根小棒。
(2)照这样摆下去:
①摆5个五边形需要多少根小棒?摆10个呢?
②用61根小棒可以摆出多少个五边形?
17.如图所示,从三个边长为1的小等边三角形开始,按螺旋式的方式依次画等边三角形,把画出的等边三角形按边长的大小由小到大排列1,1,1,2,2,3,4,5,….请你算出第21个等边三角形的边长是多少?
18.用小棒按照如图的方式摆图形.
(1)摆1个六边形需要____根小棒,摆2个需要____根小棒,摆3个需要____根小棒.
(2)照这样摆下去:
①摆n个六边形需要几根小棒?n是200时,需要几根小棒?
②181根小棒可以摆多少个六边形?
19.用若干相同的小等边三角形,可以拼成大的等边三角形.(如图所示)
(1)填写下面表格,想一想,小三角形的个数与大三角形的层数有什么关系?
(2)如果拼成的大三角形有30层.那么共用了多少个小三角形?
20.根据已知图形填出未知图形.
答案和解析
1.【答案】A;
【解析】解:3×6+1
=18+1
=19(根)
答:按这样的方法摆6个正方形共需要19根火柴.
故选:A.
2.【答案】C;
【解析】解:(10-1)×3+4
=9×3+4
=27+4
=31(根)
答:摆10个同样的正方形需要31根小棒.
故选:C.
3.【答案】B;
【解析】解:图中缺第三个图形,它一共有5个点,横看竖看都有3个点;选项中符合的只有B.
故答案选:B.
4.【答案】B;
【解析】解:第一幅图中有1个
第二幅图中有2×2-1=3(个)
第3幅图中有2×3-1=5(个)
…
可以发现,每个图形都比前一个图形多2个:
所以第n幅图有2n-1个.
故选:B.
5.【答案】B;
【解析】解:(1)1个小正方体,表面积是:6平方厘米可以写成2+1×4;
2个小正方体,表面积是10平方厘米,可以写成2+2×4;
3个小正方体,表面积是14平方厘米,可以写成2+3×4;…;
所以a个小正方体,表面积就是2+4a平方厘米;
当n=5时,表面积是:2+4×5=22(平方厘米),
故选:B.
6.【答案】C;
【解析】解:因为:
n=1时的周长:4=4+0×2
n=2时的周长:7=4+1×2
n=3时的周长:8=4+2×2
…
以此类推第n个的周长为:
4+(n-1)×2=2n+2
故选:C.
7.【答案】B;
【解析】解:观察发现,第1个图形黑点的个数是,1+3=4,
第2个图形黑点的个数是,1+3×2=7,
第3个图形黑点的个数是,1+3×3=10,
第4个图形黑点的个数是,1+3×4=13,
…
依此类推,第n个图形黑点的个数是,1+3×n=3n+1,
故选:B.
8.【答案】C;
【解析】解:(1)填表如下:
大正方形每边的块数每增加1块,所用的花瓷砖块数就增加4块;
(2)大正方形用了24块花瓷砖;
大正方形每边的块数是7,
所以中间的白瓷砖为25
答:白瓷砖用了25块.
故选:C.
9.【答案】C;
【解析】解:根据图示,可得每颗骰子相对的面对应的数是:1对6,2对5,3对4,
所以每颗骰子每个相对的面的两个数字的和是:1+6=2+5=3+4=7;
所以五颗骰子底面的点数之和是:
7×5-(5+2+1+3+5)
=35-16
=19
答:五颗骰子底面的点数之和是19.
故选:C.
10.【答案】A;
【解析】解:根据题干分析可得,第四方图形是
.
故选:A.
11.【答案】17;
【解析】解:第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△.
当n=5时,
3×5+2
=15+2
=17(个).
故答案为:17.
12.【答案】11;
【解析】解:根据题干分析所得规律:7+4=11,
所以空格内应填11.
故答案为:11.
13.【答案】42;
【解析】解:根据题干分析可得每个图中的点数个数的规律是:第n幅图中的点数为:+n;
当n=6时,点阵中的点数为:62+6=42(个);
答:第六个点阵中有42个点.
故答案为:42.
14.【答案】10;4n+2;
【解析】解:观察图形可知,第一张餐桌可以坐6人,第二张餐桌可以坐6+4=10人,…,
第n张餐桌共能坐6+4(n-1)=4n+2人,
答:2张桌子可坐 10人,n张桌子可坐 4n+2人.
故答案为:10;4n+2.
15.【答案】11;
【解析】解:1+0.8+0.6=2.4(厘米),
13÷2.4=5…1(厘米),即共经历了5个周期又多出来1厘米,
所以共有6个大正方形,5个中正方形5个小正方形,
所以这些纸片的面积之和是:
1×1×6+0.8×0.8×5+0.6×0.6×5,
=6+3.2+1.8,
=11(平方厘米);
答:这些纸片的面积之和是11平方厘米.
故答案为:11.
16.【答案】(1)5 9 13
(2)①21根 41根 ②15个;
【解析】略
17.【答案】解:根据题干分析,这组三角形的边长可以继续排列为:
1、1、1、2、2、3、4、5、7、9、12、16、21、28、37、49、65、86、114、151、200;
所以第21个三角形的边长是200.
答:第21个等边三角形的边长是200.;
【解析】观察题干中的数据“1,1,1,2,2,3,4,5,…”可得:第一个三角形的边长加第二个三角形的边长等于第四个三角形的边长,第二个三角形的边长加第三个三角形的边长等于第五个三角形的边长,第三个加第四个等于第六个,…依次排列即可得出第21个三角形的边长,由此即可解答.
18.【答案】解:根据题干分析可得:(1)摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要16根小棒,可以写成:5×3+1;…
(2)①摆n个六边形需要:5n+1根小棒,
当n=200时,需要小棒5×200+1=1001(根);
②当5n+1=181时,可以摆成的六边形有:n=(181-1)÷5=36(个);
答:摆n个六边形需要5n+1根小棒?,是200时,需要1001根小棒,181根小棒可以摆36个六边形;
故答案为:6,11,16.;
【解析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
19.【答案】解:(1)如下表,小三角形的个数是大三角形的层数的平方;
(2)共用了三角形:302=900(个);
答:(1)小三角形的个数是大三角形的层数的平方;(2)共用了900个三角形.;
【解析】(1)层数=2,小等边三角形的个数是1+3=4=22,
层数=3,小等边三角形的个数是1+3+5=9=32,
层数=4,小等边三角形的个数是1+3+5+7=16=42,
层数=5,小等边三角形的个数是1+3+5+7+9=25=52,
层数=6,小等边三角形的个数是1+3+5+7+9+11=36=62,
层数=7,小等边三角形的个数是1+3+5+7+9+11+13=49=72,
层数=8,小等边三角形的个数是1+3+5+7+9+11+13+15=64=82,
(2)如果拼成的大三角形有30层.那么共用了302.
20.【答案】解:
;
【解析】①、(1)中左上角的蓝色正方形1,在(2)中到了右上角,在(3)中到了右下角,每次转了90度,所以在(4)中应到左下角;
②、(1)中左上角的蓝色正方形2,在(2)中右移一个格,在(3)中下移一个格,每次转了90度,所以在(4)中应左移一个格;
③、(1)中在三行四列的蓝色正方形3,在(2)、(3)中每次都向左移动一个格;到(4)中即如图所示.
