华东师大版数学八年级上册 13.2.3 边角边 课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.2.3 边角边 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 12:49:40 | ||
图片预览





文档简介
(共20张PPT)
边角边
三角形全等的判定
——边角边
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
求助热线
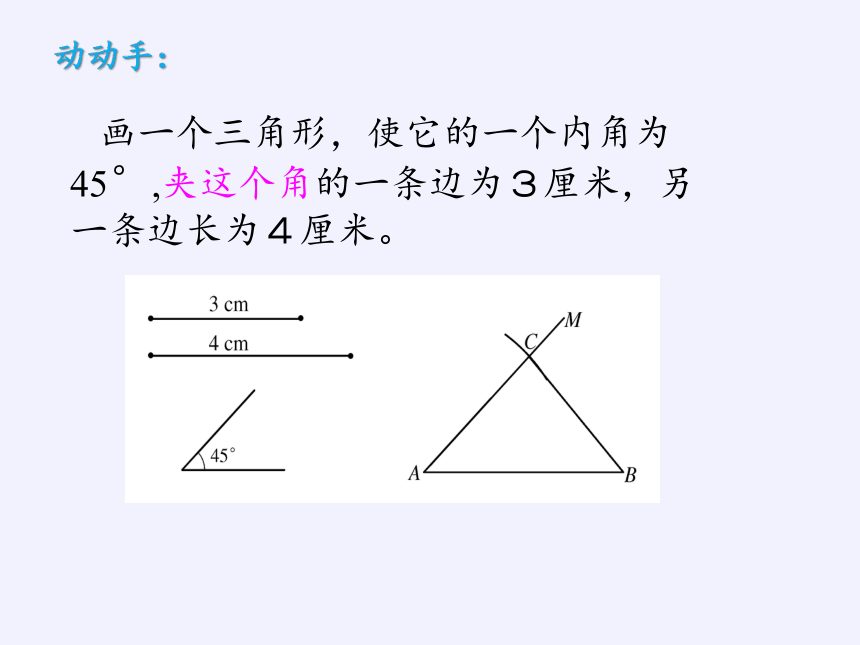
动动手:
画一个三角形,使它的一个内角为45°,夹这个角的一条边为3厘米,另一条边长为4厘米。
比一比你画的三角形
与同伴画的一定全等吗?
全等
画出的三角形全等
动动手:
小组的同学自行约定:画一个三角形,使
他们具有相同的两条线段和一个夹角。比
较一下,可以得出什么结论?
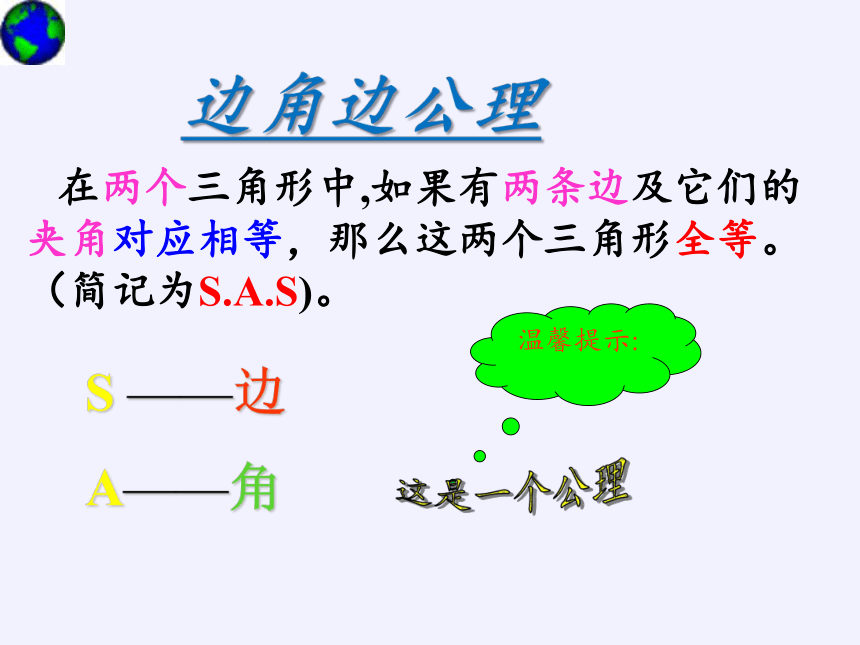
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等。(简记为S.A.S)。
温馨提示:
这是一个公理
边角边公理
S ——边
A——角
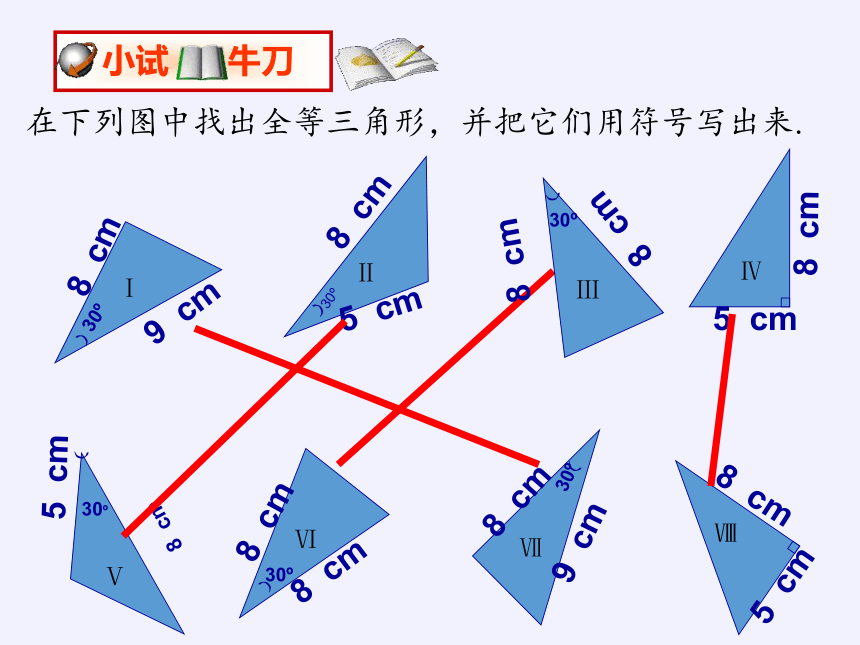
在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
小试 牛刀
C
A
B
D
O
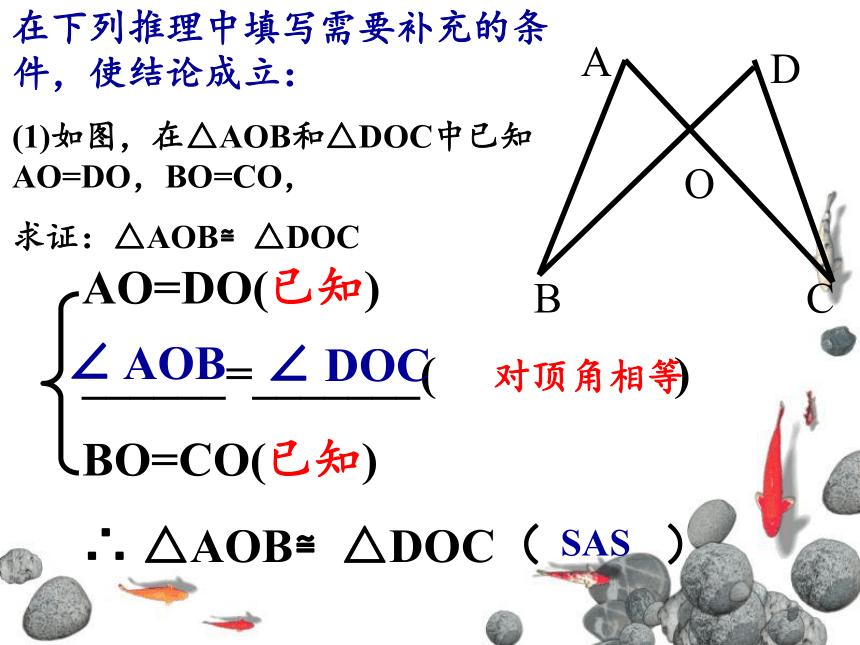
在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中已知AO=DO,BO=CO,
求证:△AOB≌△DOC
AO=DO(已知)
______=_______( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD
△ABD≌ △ACD
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
S
A
S
练习二
图中隐含
已知条件
F
A
B
D
C
E
例1:点E、F在AC上,AD//BC,AD=CB,AE=CF
求证:△AFD≌△CEB ;
分析:证三角形全等的三个条件
两直线平行,
内错角相等
∠A=∠C
边 角 边
AD // BC
AD = CB
AE = CF
AF = CE
?
(已知)
AE+EF=CF+EF
BE =DF
例题讲解
证明:
∵AD//BC
∴ ∠A=∠C
(两直线平行,内错角相等)
又∵AE=CF
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
△AFD≌△CEB(SAS)
∴AE+EF=CF+EF
即 AF=CE
摆齐根据
写出结论
F
A
B
D
C
E
指范围
准备条件
(已知)
(已证)
(已证)
∴ EB=DF
如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?
A
B
A
B
C
E
D
茅以升是这样解的:
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.
你知道为什么吗?
说一说
今天你学到了什么?
利用边角边(S.A.S.)证明三角形的全等。
证明三角形全等的过程
1、准备条件
2、指明范围
3、摆齐根据
4、写出结论
必做题:第79页习题19.2 第 2、4题;
选做题:第96页复习题 第4题。
学而时习之,不亦说乎?
A
B
C
D
E
F
有两边和其中一边的对角
对应相等的两个三角形是
否全等。
你敢挑战吗?
回去想一想
谢谢您的倾听与指导 !!
谢 谢
边角边
三角形全等的判定
——边角边
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
求助热线
动动手:
画一个三角形,使它的一个内角为45°,夹这个角的一条边为3厘米,另一条边长为4厘米。
比一比你画的三角形
与同伴画的一定全等吗?
全等
画出的三角形全等
动动手:
小组的同学自行约定:画一个三角形,使
他们具有相同的两条线段和一个夹角。比
较一下,可以得出什么结论?
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等。(简记为S.A.S)。
温馨提示:
这是一个公理
边角边公理
S ——边
A——角
在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
小试 牛刀
C
A
B
D
O
在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中已知AO=DO,BO=CO,
求证:△AOB≌△DOC
AO=DO(已知)
______=_______( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD
△ABD≌ △ACD
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
S
A
S
练习二
图中隐含
已知条件
F
A
B
D
C
E
例1:点E、F在AC上,AD//BC,AD=CB,AE=CF
求证:△AFD≌△CEB ;
分析:证三角形全等的三个条件
两直线平行,
内错角相等
∠A=∠C
边 角 边
AD // BC
AD = CB
AE = CF
AF = CE
?
(已知)
AE+EF=CF+EF
BE =DF
例题讲解
证明:
∵AD//BC
∴ ∠A=∠C
(两直线平行,内错角相等)
又∵AE=CF
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
△AFD≌△CEB(SAS)
∴AE+EF=CF+EF
即 AF=CE
摆齐根据
写出结论
F
A
B
D
C
E
指范围
准备条件
(已知)
(已证)
(已证)
∴ EB=DF
如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?
A
B
A
B
C
E
D
茅以升是这样解的:
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.
你知道为什么吗?
说一说
今天你学到了什么?
利用边角边(S.A.S.)证明三角形的全等。
证明三角形全等的过程
1、准备条件
2、指明范围
3、摆齐根据
4、写出结论
必做题:第79页习题19.2 第 2、4题;
选做题:第96页复习题 第4题。
学而时习之,不亦说乎?
A
B
C
D
E
F
有两边和其中一边的对角
对应相等的两个三角形是
否全等。
你敢挑战吗?
回去想一想
谢谢您的倾听与指导 !!
谢 谢
