华东师大版数学八年级上册 13.3.1 等腰三角形的性质 课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.3.1 等腰三角形的性质 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 12:52:04 | ||
图片预览




文档简介
(共20张PPT)
下载图片
看一看
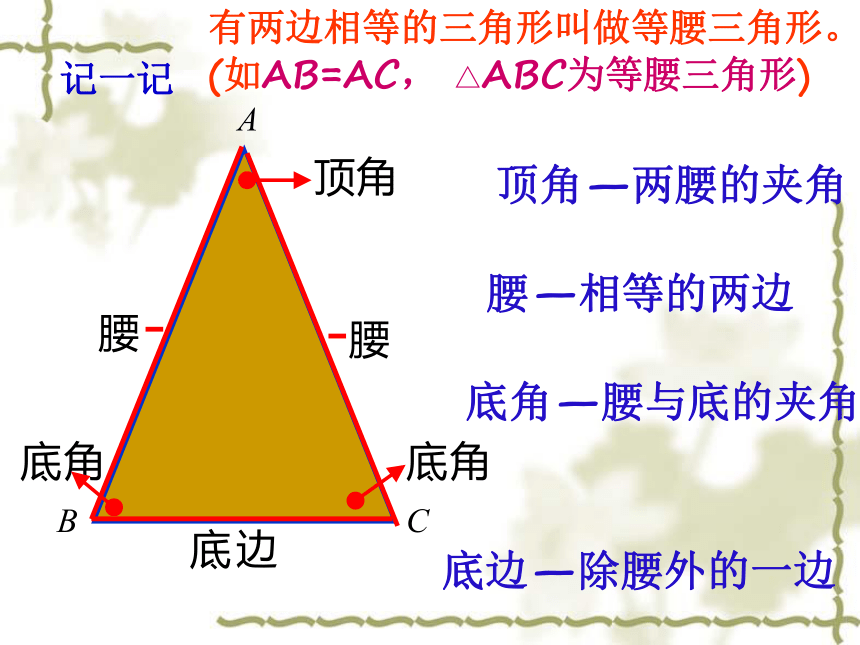
有两边相等的三角形叫做等腰三角形。
(如AB=AC, △ABC为等腰三角形)
腰—相等的两边
底边—除腰外的一边
顶角—两腰的夹角
底角—腰与底的夹角
记一记
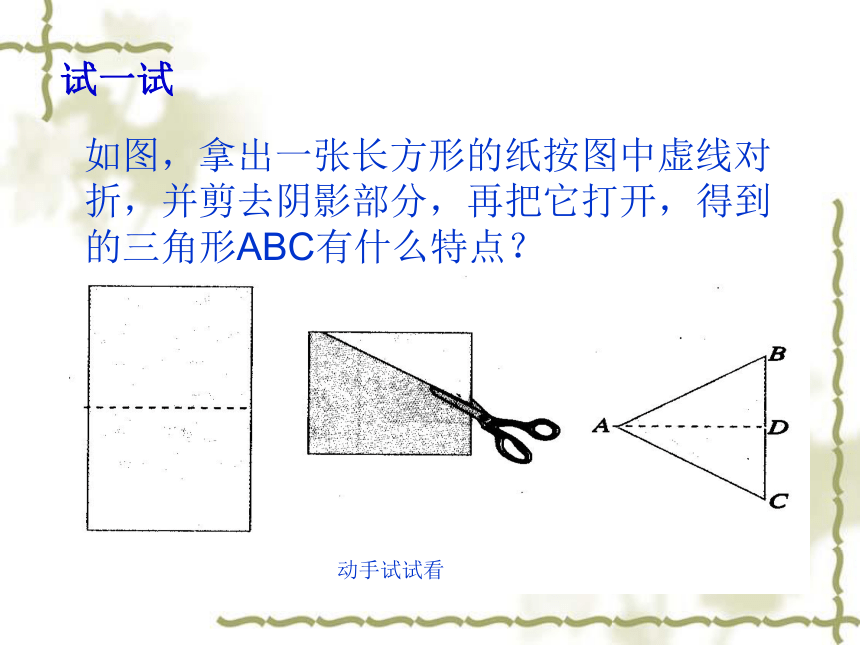
如图,拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?
动手试试看
试一试
想一想
1、上面剪出的等腰三角形是轴对称图形吗?
2、把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。
3、由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
设问:你发现了什么现象,
猜想等腰△ABC有哪些性质?
角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD
→ 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
结论: 等腰三角形是轴对称图形;
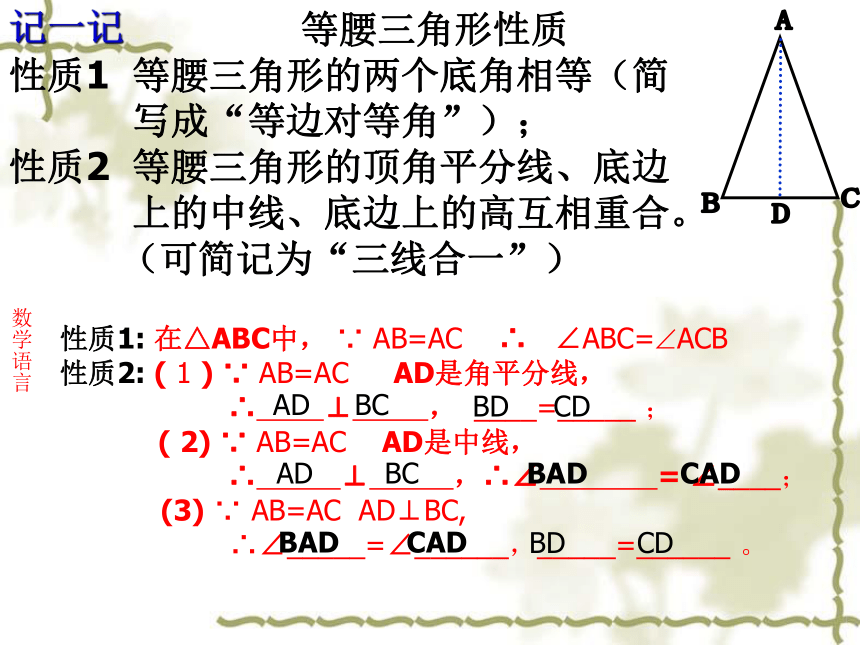
等腰三角形性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”);
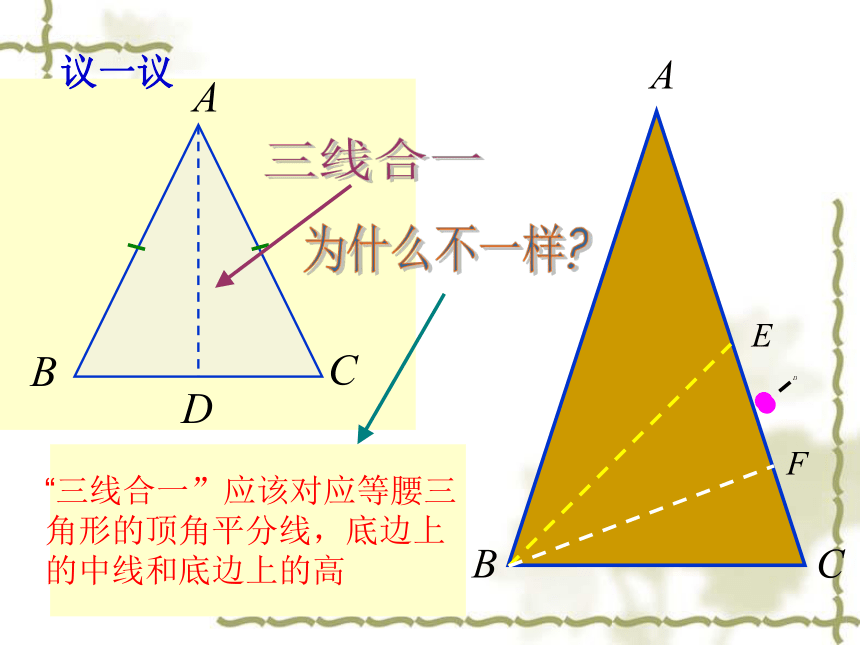
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
说一说
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
议一议
“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的
“等边对等角”必须在同一个等腰三角形中才成立
请注意哦!
等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
数学语言
性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC= ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
(3) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
记一记
A
B
C
已知:如图,在△ABC中, AB=AC,
求证:∠B=∠C。
求证:等腰三角形两底角相等
证一证
二J
三G
一Z
继续
D
已知:在△ABC中,若AB=AC,
求证:∠ABC= ACB.
∵在△BAD与△CAD 中
AB=AC
BD=CD
AD=AD ,
∴△BAD≌△CAD (SSS).
∴∠B=∠C.
证明:①作底边BC的中线AD.
A
B
C
D
② ∵ △BAD≌△CAD ∴∠BAD=∠CAD ∠ADB=∠ADC
又∵ ∠BAD+∠CAD =1800
∴∠BAD=∠CAD=900 即AD⊥BC
返回
D
已知:如图,在ΔABC中,AB=AC。
求证:∠B=∠C
A
B
C
证明:作顶角的平分线AD
② ∵ △BAD≌△CAD ∴BD=CD ∠ADB=∠ADC
又∵ ∠BAD+∠CAD =1800
∴∠BAD=∠CAD=900 即AD⊥BC
即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
返回
A
B
C
D
已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C
证明:作AD垂直BC于D。
即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中∵AB=AC AD=AD
∴ Rt △BAD≌ Rt △CAD (HL)
② ∵ Rt △BAD≌ Rt △CAD
∴ ∠BAD=∠CAD
BD=CD
返回
例1 已知:在△ABC中,AB=AC,∠B=80。求∠C和∠A的度数.
(已知)
(等边对等角)
(三角形内角和等于 )
学一学
例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30。求∠1和∠ADC的度数.
∵ AB=AC,D是BC边上的中点
∠ADC= 90。
∵ ∠BAC=180。-30。-30。=120 。
(三线合一)
学一学
练一练
1.如图,在下列等腰三角形中,分别求出其它两角的度数。
⌒
36°
⌒
108°
∟
⌒
⌒
72 °
72 °
⌒
⌒
36 °
36 °
⌒
⌒
45°
45°
2.回答。
(1)已知等腰三角形的一个底角是360,
则其余两角为_______________。
(2)已知等腰三角形的一个角是360,
则其余两角为___________________。
(3)已知等腰三角形的一个角是1100,
则其余两角为____________________。
36°,108°或72°,72°
35 °,35 °
36 °,
108°
练一练
如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠ CAD的度数,图中有哪些相等的线段?
A
C
B
∟
∟
D
45°
45°
45°
45°
相等的线段:
AB=AC
AD=BD=CD
议一议
概念:有两条边相等的三角形是等腰三角形
等腰三角形是轴对称图形,顶角平分线(或底边中线或底边上的高线)所在直线是它的对称轴.
1. 等腰三角形
2. 能根据等腰三角形的概念与性质求等腰三角形的边长、周长及其知道一角求其它两角。
谈一谈
本节课你学到了什么?
还有什么疑惑?
已知,如图AB=AC,AD=AE。
求证:BD=CE。
E
D
C
B
A
方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CE
F
∟
考一考
下载图片
看一看
有两边相等的三角形叫做等腰三角形。
(如AB=AC, △ABC为等腰三角形)
腰—相等的两边
底边—除腰外的一边
顶角—两腰的夹角
底角—腰与底的夹角
记一记
如图,拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?
动手试试看
试一试
想一想
1、上面剪出的等腰三角形是轴对称图形吗?
2、把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。
3、由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。
设问:你发现了什么现象,
猜想等腰△ABC有哪些性质?
角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD
→ 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
结论: 等腰三角形是轴对称图形;
等腰三角形性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
说一说
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
议一议
“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的
“等边对等角”必须在同一个等腰三角形中才成立
请注意哦!
等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
数学语言
性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC= ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
(3) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
记一记
A
B
C
已知:如图,在△ABC中, AB=AC,
求证:∠B=∠C。
求证:等腰三角形两底角相等
证一证
二J
三G
一Z
继续
D
已知:在△ABC中,若AB=AC,
求证:∠ABC= ACB.
∵在△BAD与△CAD 中
AB=AC
BD=CD
AD=AD ,
∴△BAD≌△CAD (SSS).
∴∠B=∠C.
证明:①作底边BC的中线AD.
A
B
C
D
② ∵ △BAD≌△CAD ∴∠BAD=∠CAD ∠ADB=∠ADC
又∵ ∠BAD+∠CAD =1800
∴∠BAD=∠CAD=900 即AD⊥BC
返回
D
已知:如图,在ΔABC中,AB=AC。
求证:∠B=∠C
A
B
C
证明:作顶角的平分线AD
② ∵ △BAD≌△CAD ∴BD=CD ∠ADB=∠ADC
又∵ ∠BAD+∠CAD =1800
∴∠BAD=∠CAD=900 即AD⊥BC
即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
返回
A
B
C
D
已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C
证明:作AD垂直BC于D。
即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中∵AB=AC AD=AD
∴ Rt △BAD≌ Rt △CAD (HL)
② ∵ Rt △BAD≌ Rt △CAD
∴ ∠BAD=∠CAD
BD=CD
返回
例1 已知:在△ABC中,AB=AC,∠B=80。求∠C和∠A的度数.
(已知)
(等边对等角)
(三角形内角和等于 )
学一学
例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30。求∠1和∠ADC的度数.
∵ AB=AC,D是BC边上的中点
∠ADC= 90。
∵ ∠BAC=180。-30。-30。=120 。
(三线合一)
学一学
练一练
1.如图,在下列等腰三角形中,分别求出其它两角的度数。
⌒
36°
⌒
108°
∟
⌒
⌒
72 °
72 °
⌒
⌒
36 °
36 °
⌒
⌒
45°
45°
2.回答。
(1)已知等腰三角形的一个底角是360,
则其余两角为_______________。
(2)已知等腰三角形的一个角是360,
则其余两角为___________________。
(3)已知等腰三角形的一个角是1100,
则其余两角为____________________。
36°,108°或72°,72°
35 °,35 °
36 °,
108°
练一练
如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠ CAD的度数,图中有哪些相等的线段?
A
C
B
∟
∟
D
45°
45°
45°
45°
相等的线段:
AB=AC
AD=BD=CD
议一议
概念:有两条边相等的三角形是等腰三角形
等腰三角形是轴对称图形,顶角平分线(或底边中线或底边上的高线)所在直线是它的对称轴.
1. 等腰三角形
2. 能根据等腰三角形的概念与性质求等腰三角形的边长、周长及其知道一角求其它两角。
谈一谈
本节课你学到了什么?
还有什么疑惑?
已知,如图AB=AC,AD=AE。
求证:BD=CE。
E
D
C
B
A
方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CE
F
∟
考一考
