华东师大版数学八年级上册 13.5.2 线段垂直平分线 课件(共17张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.5.2 线段垂直平分线 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 987.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 12:55:29 | ||
图片预览




文档简介
(共17张PPT)
线段垂直平分线
运用尺规作已知线段的垂直平分线,在垂直平分线上任意找一点,连结该点与线段的两个端点,最后沿垂直平分线对折。你发现了什么?
新课导入
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等。
推进新课
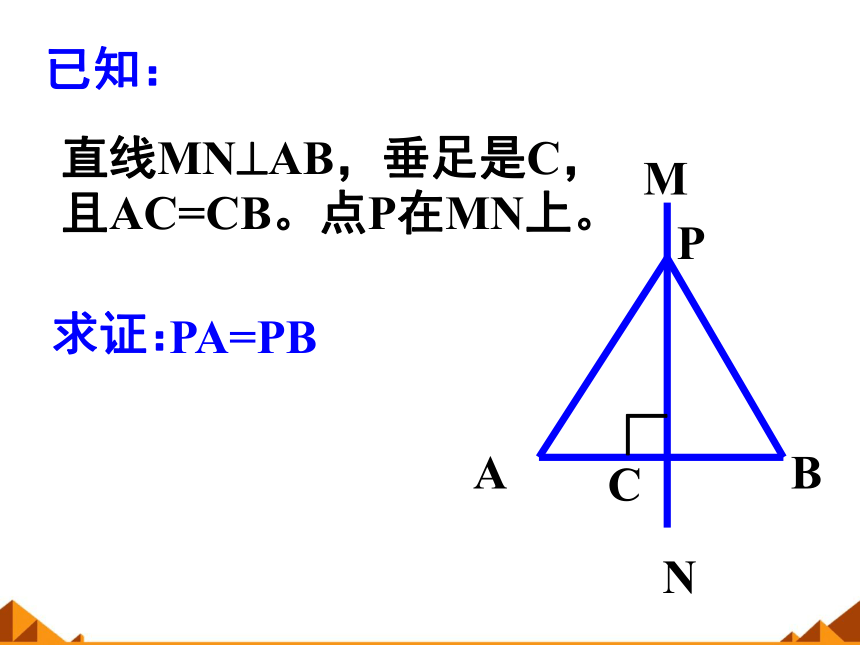
直线MN AB,垂足是C,且AC=CB。点P在MN上。
已知:
PA=PB
求证:
A
B
C
N
M
P
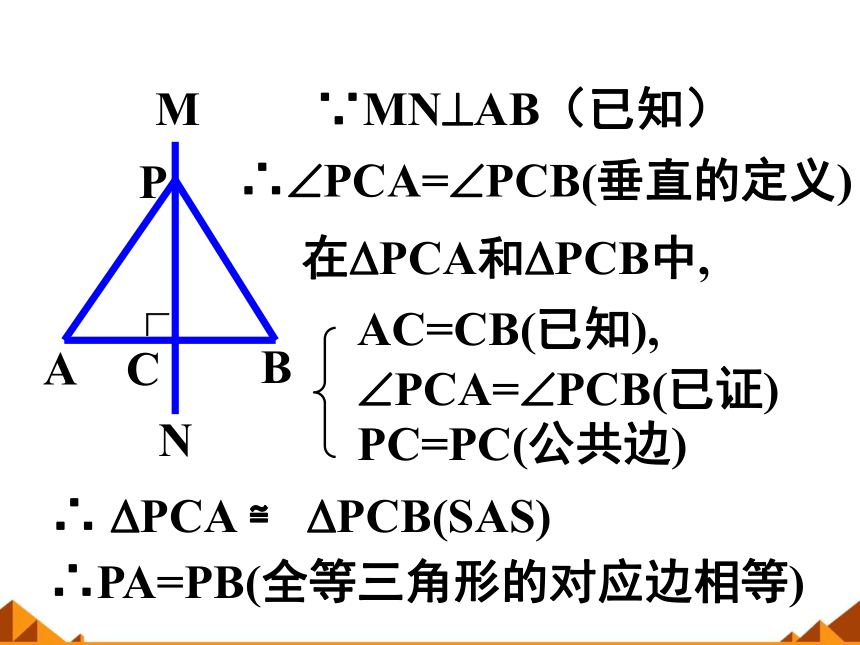
证明:
∵MN AB(已知)
∴ PCA= PCB(垂直的定义)
在 PCA和 PCB中,
AC=CB(已知),
PCA= PCB(已证)
PC=PC(公共边)
∴ PCA ≌ PCB(SAS)
∴PA=PB(全等三角形的对应边相等)
A
B
C
M
N
P
A
B
C
M
N
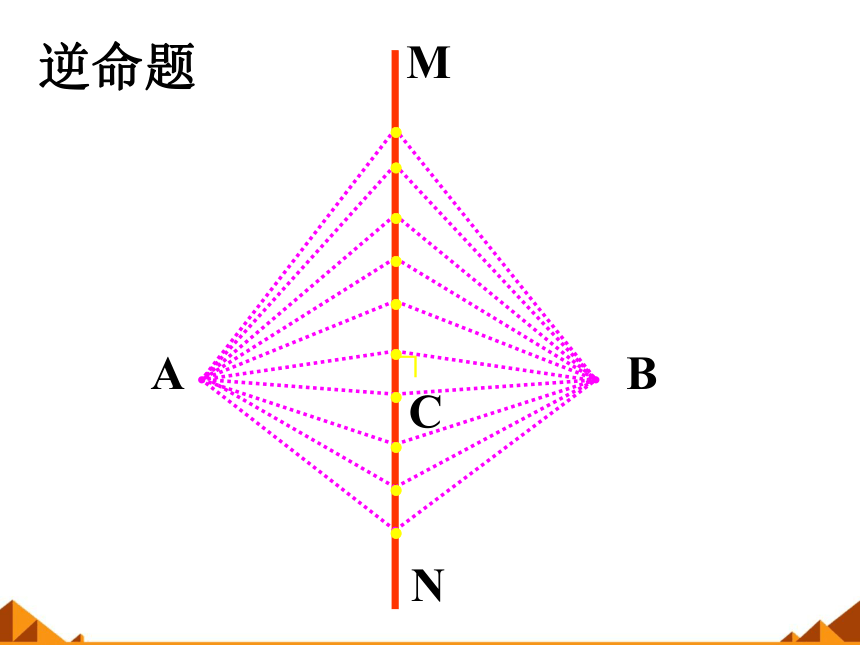
逆命题
条件 结论
性质定理
逆命题
一直线是一线段的垂直平分线
该直线上的点到线段两端的距离相等
点到线段两端的距离相等
该点在线段的垂直平分线上
B
P
C
已知:
线段AB,且PA=PB
求证:
点P在线段AB的垂直平分线MN上。
过点P作PC AB垂足为C。
∵ PA=PB(已知)
∴ PAB是等腰三角形(等腰三角 形的定义)
∴AC=BC(等腰三角形底边上的高是底边上的中线)
∴PC是线段AB的垂直平分线。
即点P在线段AB的垂直
平分线MN上。
证明:
A
到线段两端点距离相等的点在线段的垂直平分线上。
逆定理
例 已知:如图 ABC中,边AB、BC的垂直平分线相交于点P。
求证:PA=PB=PC。
∴ PA=PB(线段垂直平分线上的点和这条线段两个端点距离相等)
证明: ∵ 点A在线段AB的垂直平分线上(已知)
同理 PB=PC
∴ PA=PB=PC。
A
C
B
M
P
N
M/
N/
填空:
1。已知:如图,AD是 ABC的高,E为AD上一点,
且BE=CE,则 ABC为 三角形。
2。已知: 等腰 ABC,AB=AC,AD为BC边上的高,
E为AD上一点,则BE EC。(填>、<或=号)
A
B
C
E
D
A
B
C
E
D
1题图
2题图
等腰
=
随堂演练
3。已知:如图,AB=AC, A=30o,AB的垂直平分线MN交AC于D,则 1= , 2= 。
A
B
C
D
M
N
30o
1
2
75o
30o
60o
45o
2
填空:
4。已知:如图,在 ABC中,DE是AC的垂直平分线,
AE=3cm, ABD的周长为13cm,则 ABC 的周长
为 cm
A
B
D
C
E
3cm
3cm
19
13cm
5。如图,CD、EF分别是AB、BC的垂直平分线。请你指出图中相等的线段有哪些
AD =BD
CF = BF
AC = BC
CE = BE
1
2
3
CF =DF
即:BF=CF=DF
A
C
E
B
F
D
小结:
1。线段的垂直平分线上的点,到这条线段两个端点的距离相等。
2。到一条线段两个端点距离相等的 点,在这条线段的垂直平分线上。
互
逆
命
题
课堂小结
这节课你有哪些收获?你觉得还有哪些地方存在疑问,不妨与同伴交流。
如果学习只在于模仿,那么我们就不会有科学,也不会有技术。
——高尔基
线段垂直平分线
运用尺规作已知线段的垂直平分线,在垂直平分线上任意找一点,连结该点与线段的两个端点,最后沿垂直平分线对折。你发现了什么?
新课导入
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等。
推进新课
直线MN AB,垂足是C,且AC=CB。点P在MN上。
已知:
PA=PB
求证:
A
B
C
N
M
P
证明:
∵MN AB(已知)
∴ PCA= PCB(垂直的定义)
在 PCA和 PCB中,
AC=CB(已知),
PCA= PCB(已证)
PC=PC(公共边)
∴ PCA ≌ PCB(SAS)
∴PA=PB(全等三角形的对应边相等)
A
B
C
M
N
P
A
B
C
M
N
逆命题
条件 结论
性质定理
逆命题
一直线是一线段的垂直平分线
该直线上的点到线段两端的距离相等
点到线段两端的距离相等
该点在线段的垂直平分线上
B
P
C
已知:
线段AB,且PA=PB
求证:
点P在线段AB的垂直平分线MN上。
过点P作PC AB垂足为C。
∵ PA=PB(已知)
∴ PAB是等腰三角形(等腰三角 形的定义)
∴AC=BC(等腰三角形底边上的高是底边上的中线)
∴PC是线段AB的垂直平分线。
即点P在线段AB的垂直
平分线MN上。
证明:
A
到线段两端点距离相等的点在线段的垂直平分线上。
逆定理
例 已知:如图 ABC中,边AB、BC的垂直平分线相交于点P。
求证:PA=PB=PC。
∴ PA=PB(线段垂直平分线上的点和这条线段两个端点距离相等)
证明: ∵ 点A在线段AB的垂直平分线上(已知)
同理 PB=PC
∴ PA=PB=PC。
A
C
B
M
P
N
M/
N/
填空:
1。已知:如图,AD是 ABC的高,E为AD上一点,
且BE=CE,则 ABC为 三角形。
2。已知: 等腰 ABC,AB=AC,AD为BC边上的高,
E为AD上一点,则BE EC。(填>、<或=号)
A
B
C
E
D
A
B
C
E
D
1题图
2题图
等腰
=
随堂演练
3。已知:如图,AB=AC, A=30o,AB的垂直平分线MN交AC于D,则 1= , 2= 。
A
B
C
D
M
N
30o
1
2
75o
30o
60o
45o
2
填空:
4。已知:如图,在 ABC中,DE是AC的垂直平分线,
AE=3cm, ABD的周长为13cm,则 ABC 的周长
为 cm
A
B
D
C
E
3cm
3cm
19
13cm
5。如图,CD、EF分别是AB、BC的垂直平分线。请你指出图中相等的线段有哪些
AD =BD
CF = BF
AC = BC
CE = BE
1
2
3
CF =DF
即:BF=CF=DF
A
C
E
B
F
D
小结:
1。线段的垂直平分线上的点,到这条线段两个端点的距离相等。
2。到一条线段两个端点距离相等的 点,在这条线段的垂直平分线上。
互
逆
命
题
课堂小结
这节课你有哪些收获?你觉得还有哪些地方存在疑问,不妨与同伴交流。
如果学习只在于模仿,那么我们就不会有科学,也不会有技术。
——高尔基
