冀教版数学七年级上册 第二章 几何图形的初步认识 复习(共16张)
文档属性
| 名称 | 冀教版数学七年级上册 第二章 几何图形的初步认识 复习(共16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 564.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 14:03:13 | ||
图片预览





文档简介
(共16张PPT)
第二章 几何图形的初步认识
复习课件
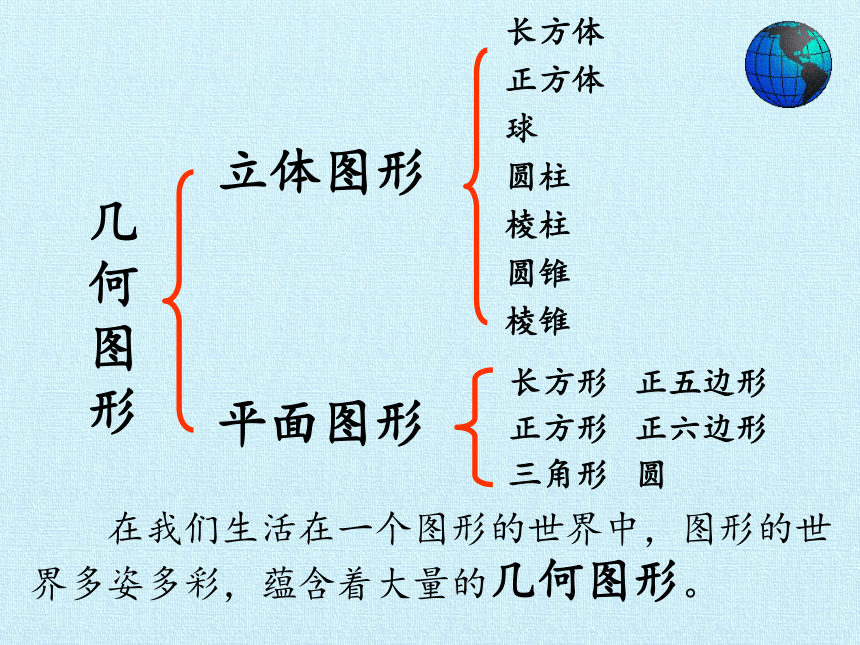
几何图形
立体图形
平面图形
长方形 正五边形
正方形 正六边形
三角形 圆
长方体
正方体
球
圆柱
棱柱
圆锥
棱锥
在我们生活在一个图形的世界中,图形的世界多姿多彩,蕴含着大量的几何图形。
点
线
角
1.抽象的概念,没有大小
2.表示方法:一个大写字母
是否可量
直线,射线
线段
1.概念
2.表示方法
3.角的大小的比较方法
4.角的运算
5.两角互余 互补
1.表示方法
2.区别,联系
3.和点的位置关系
1.表示方法
2.比较大小
图形的旋转
对应点到旋转中心的距离相等
每对对应点与旋转中心的连线所成的角都等于旋转角
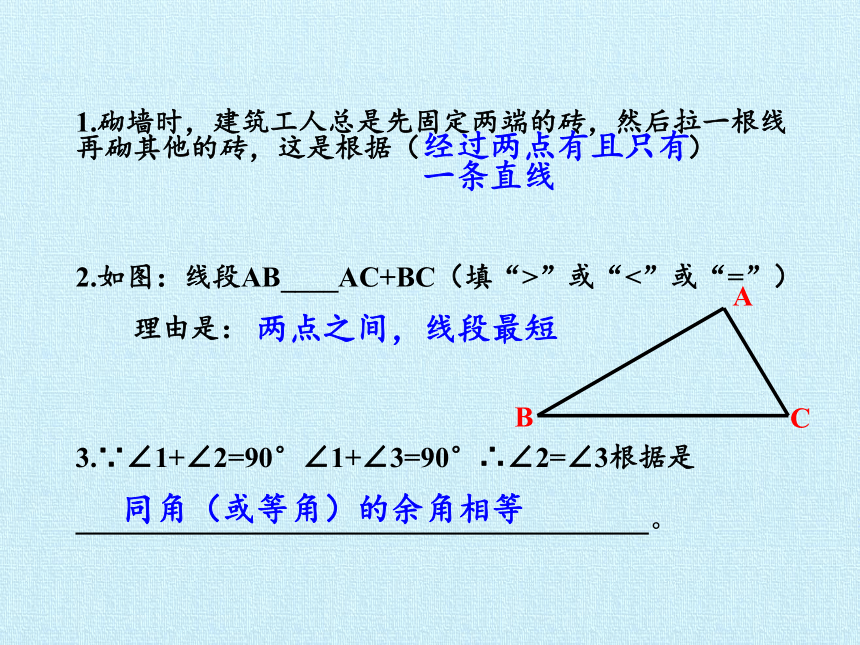
1.砌墙时,建筑工人总是先固定两端的砖,然后拉一根线
再砌其他的砖,这是根据( )
2.如图:线段AB____AC+BC(填“>”或“<”或“=”)
理由是:
3.∵∠1+∠2=90°∠1+∠3=90°∴∠2=∠3根据是
。
A
B
C
经过两点有且只有一条直线
两点之间,线段最短
同角(或等角)的余角相等
三个重要结论:
1.关于直线的:
经过两点有且只有一条直线
2.关于线段的:
两点之间,线段最短
3.关于两角的关系的:
同角(或等角)的余角相等
同角(或等角)的补角相等
达标检测
1.圆锥由_________个面围成,其中______个
是平的,________个是曲的。
2.圆柱共有_______个面,底面与侧面相交成
_______条_______线。
3. 圆锥的侧面与底面相交成_______条_____线。
2
1
1
3
1
曲
1
曲
4.①飞机飞行表演在空中留下漂亮的“彩带”用数学知识解释为______________。
②把一张纸对折,形成一条折痕,用数学
知识解释为_______________。
点动成线
面面相交形成线
5.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连。
6.四棱柱有____个面,____条棱,___个顶点。
五棱柱有____个面,____条棱,___个顶点。
六棱柱有____个面,____条棱,___个顶点。
12棱柱有____个面,____条棱,____个顶点。
那么n棱柱有____个面,____条棱,____个顶点。
6
12
8
7
15
10
18
8
14
36
24
12
n+2
3n
2n
7.将长方体的每一个角切掉,其中两个角的切法如图所示,这样得到的新图形边数为( )
A.24 B.30 C. 36 D.42 E. 48
C
8.把一张长方形的纸的四
个角同时剪去一个相同的
小正方形,然后把四边卷
起来,则形成的立体图
形是___________。
9.________展开图是一个长方形和两个圆的组合。
圆柱
无盖长方体
11.图是由四个相同的小长方体堆成的物体,试
画出分别从正面、左面、上面看这个物体所
得到的平面图。
10.如图所示,从正面看、左面看、上面看得到
的图形依次为图中的( )
正
面
看
上面看
左面看
A
12.一个画家将10个棱长是1cm的小正方体,
在地面上组成如图所示的几何体。然后她把
露出的表面都染上颜色,问有_______平
方厘米被她染上颜色。
解:
前面有3×6=18个小正方
形。后面有6×2=12个小
正方形。所以一共有30个
面被染色。而一个面是1×1=1(平方厘米),故有30×1=30(平方厘米)
13.某厨师把一块棱长为10cm的正方体的豆
腐切成棱长为2cm的小正方体。一盘可装25个。
这样的小正方体豆腐,那么棱长为10cm的正方
体豆腐可装多少盘?
解:10×10×10÷(2×2×2)=125(个),125÷25=5(盘)。
答:可以装5盘。
谢 谢
第二章 几何图形的初步认识
复习课件
几何图形
立体图形
平面图形
长方形 正五边形
正方形 正六边形
三角形 圆
长方体
正方体
球
圆柱
棱柱
圆锥
棱锥
在我们生活在一个图形的世界中,图形的世界多姿多彩,蕴含着大量的几何图形。
点
线
角
1.抽象的概念,没有大小
2.表示方法:一个大写字母
是否可量
直线,射线
线段
1.概念
2.表示方法
3.角的大小的比较方法
4.角的运算
5.两角互余 互补
1.表示方法
2.区别,联系
3.和点的位置关系
1.表示方法
2.比较大小
图形的旋转
对应点到旋转中心的距离相等
每对对应点与旋转中心的连线所成的角都等于旋转角
1.砌墙时,建筑工人总是先固定两端的砖,然后拉一根线
再砌其他的砖,这是根据( )
2.如图:线段AB____AC+BC(填“>”或“<”或“=”)
理由是:
3.∵∠1+∠2=90°∠1+∠3=90°∴∠2=∠3根据是
。
A
B
C
经过两点有且只有一条直线
两点之间,线段最短
同角(或等角)的余角相等
三个重要结论:
1.关于直线的:
经过两点有且只有一条直线
2.关于线段的:
两点之间,线段最短
3.关于两角的关系的:
同角(或等角)的余角相等
同角(或等角)的补角相等
达标检测
1.圆锥由_________个面围成,其中______个
是平的,________个是曲的。
2.圆柱共有_______个面,底面与侧面相交成
_______条_______线。
3. 圆锥的侧面与底面相交成_______条_____线。
2
1
1
3
1
曲
1
曲
4.①飞机飞行表演在空中留下漂亮的“彩带”用数学知识解释为______________。
②把一张纸对折,形成一条折痕,用数学
知识解释为_______________。
点动成线
面面相交形成线
5.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连。
6.四棱柱有____个面,____条棱,___个顶点。
五棱柱有____个面,____条棱,___个顶点。
六棱柱有____个面,____条棱,___个顶点。
12棱柱有____个面,____条棱,____个顶点。
那么n棱柱有____个面,____条棱,____个顶点。
6
12
8
7
15
10
18
8
14
36
24
12
n+2
3n
2n
7.将长方体的每一个角切掉,其中两个角的切法如图所示,这样得到的新图形边数为( )
A.24 B.30 C. 36 D.42 E. 48
C
8.把一张长方形的纸的四
个角同时剪去一个相同的
小正方形,然后把四边卷
起来,则形成的立体图
形是___________。
9.________展开图是一个长方形和两个圆的组合。
圆柱
无盖长方体
11.图是由四个相同的小长方体堆成的物体,试
画出分别从正面、左面、上面看这个物体所
得到的平面图。
10.如图所示,从正面看、左面看、上面看得到
的图形依次为图中的( )
正
面
看
上面看
左面看
A
12.一个画家将10个棱长是1cm的小正方体,
在地面上组成如图所示的几何体。然后她把
露出的表面都染上颜色,问有_______平
方厘米被她染上颜色。
解:
前面有3×6=18个小正方
形。后面有6×2=12个小
正方形。所以一共有30个
面被染色。而一个面是1×1=1(平方厘米),故有30×1=30(平方厘米)
13.某厨师把一块棱长为10cm的正方体的豆
腐切成棱长为2cm的小正方体。一盘可装25个。
这样的小正方体豆腐,那么棱长为10cm的正方
体豆腐可装多少盘?
解:10×10×10÷(2×2×2)=125(个),125÷25=5(盘)。
答:可以装5盘。
谢 谢
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
