八年级数学积的乘方1
图片预览



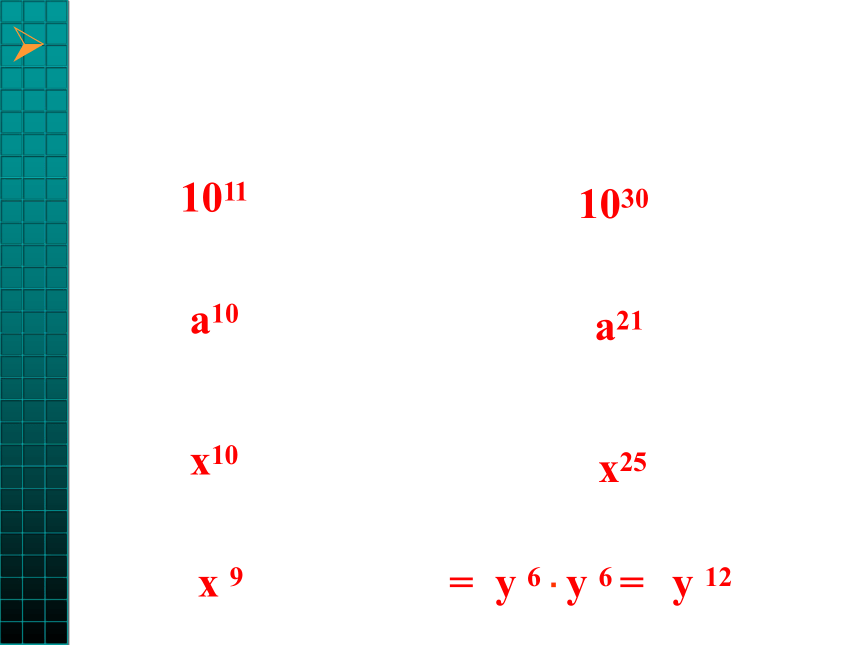




文档简介
课件20张PPT。15.1.3 积的乘方郧县安阳镇初级中学 龚频 2、唤起你的记忆:
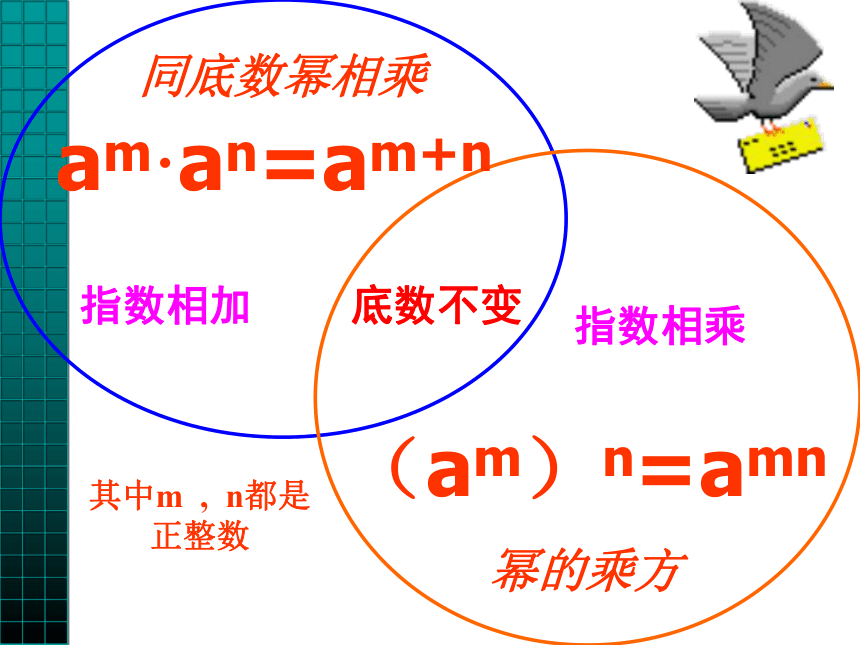
(1)叙述同底数幂乘法法则并用字母 表示。 同底数幂相乘,底数不变,指数相加。
am·an=am+n ( m、n都为正整数) 1、计算: 10×102× 103 (x5 )2一.复习回顾:(2).叙述幂的乘方法则 并用字母表示幂的乘方,底数不变,指数相乘。
(am)n=amn (m,n都是正整数)
底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n 比一比: 1.???计算:( 口答)1011 a10 x10 x 9 (3) a7 ·a3(5) x5 ·x5 (7) x5 ·x ·x3 (1) 105×106(2) (105)6(4) (a7)3 (6) (x5)5 (8)(y3)2· (y2)31030 a21 x25 y 12= y 6 · y 6 =①10m·10m-1·100=②3×27×9×3m= 2.???计算:③(m-n)4·(m-n) 5·(n-m)6
=④ (x-2y)4·(2y-x) 5·(x-2y)6
=1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xmc 相信你能行:2.x14不可以写成( )
(A)x5(x3)3 (B) (-x)(-x2)(-x3)(-x8)
(C)(x7)7 (D)x3x4x5x2c3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310 (D) -2×37B1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672开动脑筋!(1)(ab)2 = (ab) ? (ab) = (aa) ? (bb) = a ( )b( )
(2)(ab)3=__________________________
=__________________________
= a ( )b( )
(3)(ab)4=__________________________
=__________________________
= a ( )b( )(ab) ? (ab) ? (ab) (aaa) ? (bbb)22(ab) ? (ab) ? (ab) ? (ab) (aaaa) ? (bbbb)3344 【学习探究】积的乘方 试猜想:(ab)n=?
其中 n是正整数积的乘方 (ab)n =
=
= a nbn
? ∴(ab)n = a nbn (n为正整数)证明:语言叙述:积的乘方,等于把积的每个因式分别乘方,再把所得的幂相乘。(ab).(ab)…(ab)n个(a.a…a)(b.b…b)n个n个例3 计算:解(1)(2b)3(2)(2×a3)2(3)(-a)3(4)(-3x)4 =23b3
=8b3 =22×(a3)2
=4a6 =(-1)3 ?a3
= -a3 =(-3)4 ? x4
= 81 x41.判断下列计算是否正确,并说明理由:
(1)(xy3)2=xy6
(2)(-2x)3=-2x32.计算:
(1)(3a)2
(2)(-3a)3
(3)(ab2)2
(4)(-2×103)3x3y6-8x3=(-3)3a3=-27a3=a2(b2)2=a2b4=(-2)3×(103)3=-8×109=32a2=9a2逆 用 法 则 进 行 计 算 (1)24×44×0.1254
=
= (2)(-4)2005×(0.25)2005
=
=(2×4×0.125)4 1(-4×0.25)2005-1 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。
推广:
三个或三个以上的积的乘方等于什么?(abc)n = anbncn (n为正整数)课堂测验①(5ab)2
②(-xy2)3
③(-2xy3)4
④(-2×10) 3
⑤(-3x3)2-[(2x)2]3⑥(-3a3b2c)4
⑦(-anbn+1)3
⑧0.52005×22005
⑨ (-0.25)3×26
⑩ (-0.125) 8×230计 算 :小结:
1、本节课的主要内容: 幂的运算的三个性质:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都为正整数)2、 运用积的乘方法则时要注意什么?每一个因式都要“乘方”,还有符号问题。积的乘方 板书设计1.积的乘方:等于把积的每个因式分别乘方,再把所得的幂相乘。
(ab)n = a nbn (n为正整数)
2.逆用: anbn = (ab)n
3.推广:(abc)n = anbncn (n为正整数)
布置作业:1.导学练案
2.教材149页第3题谢谢!
(1)叙述同底数幂乘法法则并用字母 表示。 同底数幂相乘,底数不变,指数相加。
am·an=am+n ( m、n都为正整数) 1、计算: 10×102× 103 (x5 )2一.复习回顾:(2).叙述幂的乘方法则 并用字母表示幂的乘方,底数不变,指数相乘。
(am)n=amn (m,n都是正整数)
底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n 比一比: 1.???计算:( 口答)1011 a10 x10 x 9 (3) a7 ·a3(5) x5 ·x5 (7) x5 ·x ·x3 (1) 105×106(2) (105)6(4) (a7)3 (6) (x5)5 (8)(y3)2· (y2)31030 a21 x25 y 12= y 6 · y 6 =①10m·10m-1·100=②3×27×9×3m= 2.???计算:③(m-n)4·(m-n) 5·(n-m)6
=④ (x-2y)4·(2y-x) 5·(x-2y)6
=1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xmc 相信你能行:2.x14不可以写成( )
(A)x5(x3)3 (B) (-x)(-x2)(-x3)(-x8)
(C)(x7)7 (D)x3x4x5x2c3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310 (D) -2×37B1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672开动脑筋!(1)(ab)2 = (ab) ? (ab) = (aa) ? (bb) = a ( )b( )
(2)(ab)3=__________________________
=__________________________
= a ( )b( )
(3)(ab)4=__________________________
=__________________________
= a ( )b( )(ab) ? (ab) ? (ab) (aaa) ? (bbb)22(ab) ? (ab) ? (ab) ? (ab) (aaaa) ? (bbbb)3344 【学习探究】积的乘方 试猜想:(ab)n=?
其中 n是正整数积的乘方 (ab)n =
=
= a nbn
? ∴(ab)n = a nbn (n为正整数)证明:语言叙述:积的乘方,等于把积的每个因式分别乘方,再把所得的幂相乘。(ab).(ab)…(ab)n个(a.a…a)(b.b…b)n个n个例3 计算:解(1)(2b)3(2)(2×a3)2(3)(-a)3(4)(-3x)4 =23b3
=8b3 =22×(a3)2
=4a6 =(-1)3 ?a3
= -a3 =(-3)4 ? x4
= 81 x41.判断下列计算是否正确,并说明理由:
(1)(xy3)2=xy6
(2)(-2x)3=-2x32.计算:
(1)(3a)2
(2)(-3a)3
(3)(ab2)2
(4)(-2×103)3x3y6-8x3=(-3)3a3=-27a3=a2(b2)2=a2b4=(-2)3×(103)3=-8×109=32a2=9a2逆 用 法 则 进 行 计 算 (1)24×44×0.1254
=
= (2)(-4)2005×(0.25)2005
=
=(2×4×0.125)4 1(-4×0.25)2005-1 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。
推广:
三个或三个以上的积的乘方等于什么?(abc)n = anbncn (n为正整数)课堂测验①(5ab)2
②(-xy2)3
③(-2xy3)4
④(-2×10) 3
⑤(-3x3)2-[(2x)2]3⑥(-3a3b2c)4
⑦(-anbn+1)3
⑧0.52005×22005
⑨ (-0.25)3×26
⑩ (-0.125) 8×230计 算 :小结:
1、本节课的主要内容: 幂的运算的三个性质:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都为正整数)2、 运用积的乘方法则时要注意什么?每一个因式都要“乘方”,还有符号问题。积的乘方 板书设计1.积的乘方:等于把积的每个因式分别乘方,再把所得的幂相乘。
(ab)n = a nbn (n为正整数)
2.逆用: anbn = (ab)n
3.推广:(abc)n = anbncn (n为正整数)
布置作业:1.导学练案
2.教材149页第3题谢谢!
