八年级数学全等三角形学案
文档属性
| 名称 | 八年级数学全等三角形学案 |  | |
| 格式 | zip | ||
| 文件大小 | 121.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 11:52:03 | ||
图片预览

文档简介
第五章 三角形
知识回顾:
三角形两边之和______第三边,两边之差_____第三边.
三条线段a,b,c,若c为最长线段,如果,则能围成三角形。
在求解等腰三角形时,要分两钟情况讨论,并检验是否满足三边关系。
三角形内角和________.(n边形内角和______)
三角形分为___________,___________,_____________.
直角三角形中两锐_______.
特殊线段:角平分线、高线、中线。三条中线、角平分线交与一点。
三角形________把三角形分成两个面积相等的三角形。
如图,在中, ,的平分线交与点O,则
题型归纳:
求第三边取值范围。
在中,,则。
一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是_____.
一个等腰三角形的一边长是5cm,另一边长是7cm,则这个三角形周长是______.
从长度为2、3、4、5的四条线段中,任选3条,能组成三角形的概率是____.
如图所示,在 中,D是AB上的一点,则成立吗?说明你的理由。
如图所示,在中,在,,则图中互余的角有多少对?相等的锐角有多少对?
新知讲解:全等三角形及其sss判定条件。
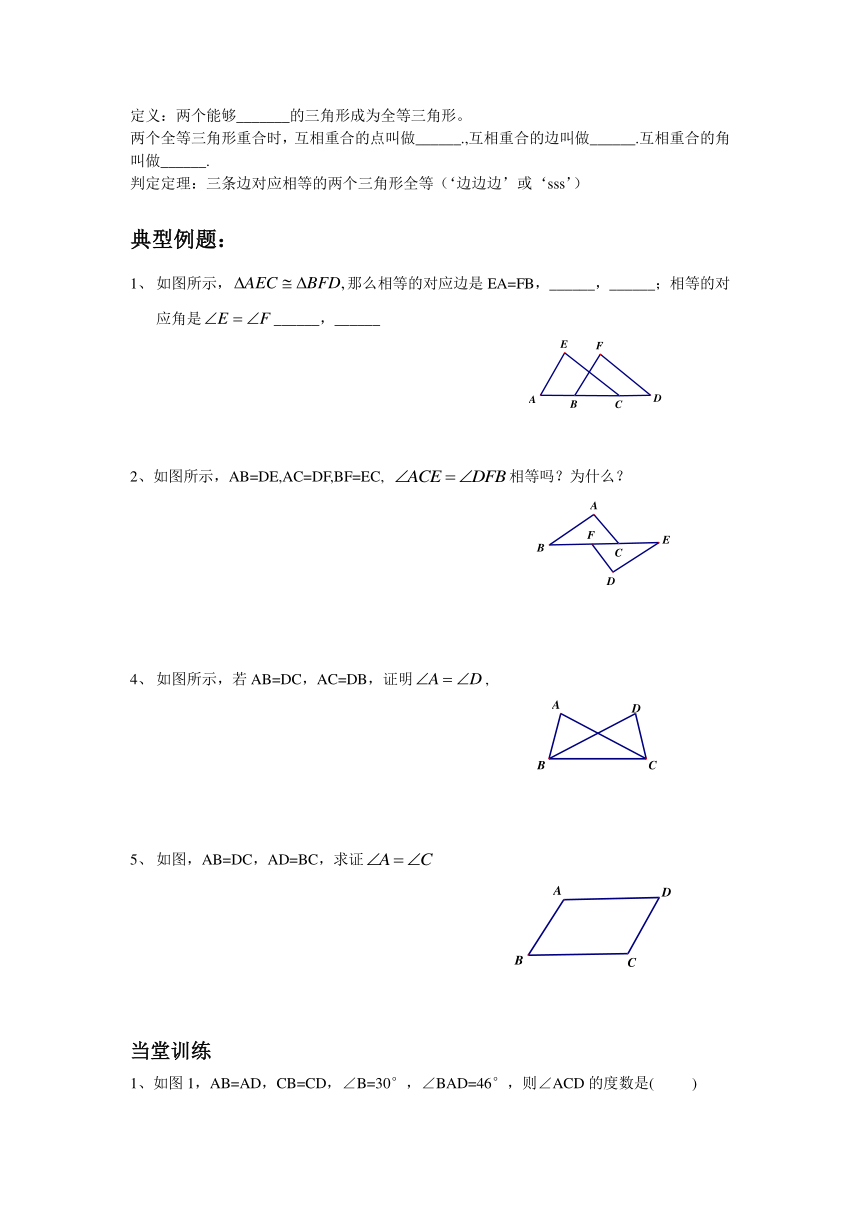
定义:两个能够_______的三角形成为全等三角形。
两个全等三角形重合时,互相重合的点叫做______.,互相重合的边叫做______.互相重合的角叫做______.
判定定理:三条边对应相等的两个三角形全等(‘边边边’或‘sss’)
典型例题:
如图所示,那么相等的对应边是EA=FB,______,______;相等的对应角是______,______
2、如图所示,AB=DE,AC=DF,BF=EC, 相等吗?为什么?
如图所示,若AB=DC,AC=DB,证明,
如图,AB=DC,AD=BC,求证
当堂训练
1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是( )
A.△ABC≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D
3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.
4、如图,AB=AC,BD=CD,求证:∠1=∠2.
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.
6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.
7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
⑴请你添加一个条件,使△DEC≌△BFA;
⑵在⑴的基础上,求证:DE∥BF.
作业:
下列一定全等的三角形是()
A、面积相等的三角形 B周长相等的三角形
C 形状相同的三角形 D能够完全重合的两个三角形
2、如图所示,在平行四边形ABCD的对角线AC,BD相交与点O,那么图中全等三角形共有( )
A、1对 B、2对 C、3对 D、4对
2、如图所示,已知绕点A顺时针旋转20后得到
(1)和有何关系?
(2)求的度数。
(3)若,,将绕顶点A顺时针旋转多少度时,旋转后的
的顶点E与原的顶点B和A在同一直线上。
3、已知如图所示,AE=DF,B、C是AD上的点,且AB=CD,EC=FB,AE与DF平行吗?为什么?
在长方形ABCD中,E、F是BC上的点,且BE=CF,AF=DE,求证:。
如图,已知D是BC的中点,AB=AC,BE=CE,图中有几对全等三角形,请选一对加以证明。
知识回顾:
三角形两边之和______第三边,两边之差_____第三边.
三条线段a,b,c,若c为最长线段,如果,则能围成三角形。
在求解等腰三角形时,要分两钟情况讨论,并检验是否满足三边关系。
三角形内角和________.(n边形内角和______)
三角形分为___________,___________,_____________.
直角三角形中两锐_______.
特殊线段:角平分线、高线、中线。三条中线、角平分线交与一点。
三角形________把三角形分成两个面积相等的三角形。
如图,在中, ,的平分线交与点O,则
题型归纳:
求第三边取值范围。
在中,,则。
一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是_____.
一个等腰三角形的一边长是5cm,另一边长是7cm,则这个三角形周长是______.
从长度为2、3、4、5的四条线段中,任选3条,能组成三角形的概率是____.
如图所示,在 中,D是AB上的一点,则成立吗?说明你的理由。
如图所示,在中,在,,则图中互余的角有多少对?相等的锐角有多少对?
新知讲解:全等三角形及其sss判定条件。
定义:两个能够_______的三角形成为全等三角形。
两个全等三角形重合时,互相重合的点叫做______.,互相重合的边叫做______.互相重合的角叫做______.
判定定理:三条边对应相等的两个三角形全等(‘边边边’或‘sss’)
典型例题:
如图所示,那么相等的对应边是EA=FB,______,______;相等的对应角是______,______
2、如图所示,AB=DE,AC=DF,BF=EC, 相等吗?为什么?
如图所示,若AB=DC,AC=DB,证明,
如图,AB=DC,AD=BC,求证
当堂训练
1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C.127° D.104°
2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是( )
A.△ABC≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D
3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.
4、如图,AB=AC,BD=CD,求证:∠1=∠2.
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.
6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.
7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.
⑴请你添加一个条件,使△DEC≌△BFA;
⑵在⑴的基础上,求证:DE∥BF.
作业:
下列一定全等的三角形是()
A、面积相等的三角形 B周长相等的三角形
C 形状相同的三角形 D能够完全重合的两个三角形
2、如图所示,在平行四边形ABCD的对角线AC,BD相交与点O,那么图中全等三角形共有( )
A、1对 B、2对 C、3对 D、4对
2、如图所示,已知绕点A顺时针旋转20后得到
(1)和有何关系?
(2)求的度数。
(3)若,,将绕顶点A顺时针旋转多少度时,旋转后的
的顶点E与原的顶点B和A在同一直线上。
3、已知如图所示,AE=DF,B、C是AD上的点,且AB=CD,EC=FB,AE与DF平行吗?为什么?
在长方形ABCD中,E、F是BC上的点,且BE=CF,AF=DE,求证:。
如图,已知D是BC的中点,AB=AC,BE=CE,图中有几对全等三角形,请选一对加以证明。
