2021-2022学年青岛版九年级数学下册 5.2反比例函数与三角形面积专题(Word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学下册 5.2反比例函数与三角形面积专题(Word版含解析) | 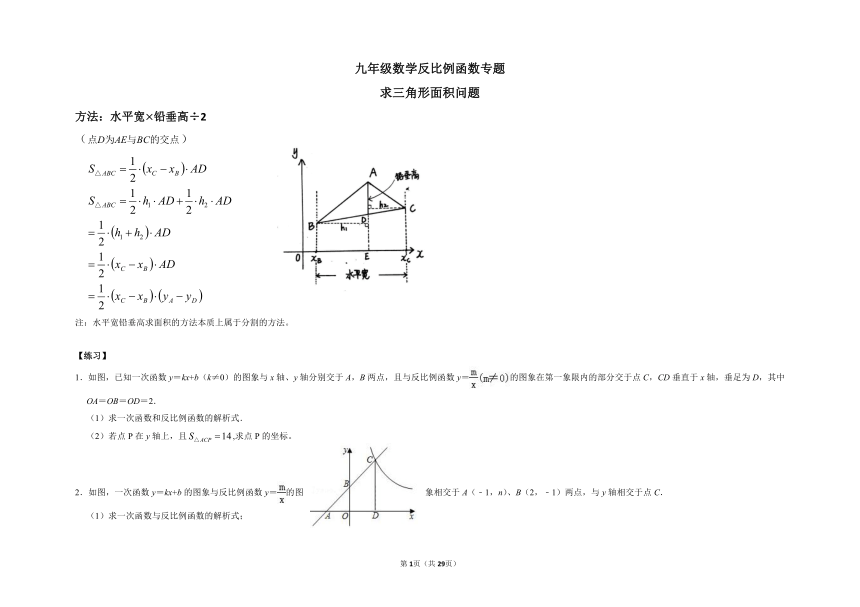 | |
| 格式 | docx | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 14:35:18 | ||
图片预览





文档简介
九年级数学反比例函数专题
求三角形面积问题
方法:水平宽铅垂高÷2
()
注:水平宽铅垂高求面积的方法本质上属于分割的方法。
【练习】
1.如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=的图象在第一象限内的部分交于点C,CD垂直于x轴,垂足为D,其中OA=OB=OD=2.
(1)求一次函数和反比例函数的解析式.
(2)若点P在y轴上,且,求点P的坐标。
2.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)当时,直接写出自变量x的取值范围。
(3)若点D与点C关于x轴对称,点P为y轴上一点,且S△ABD=S△ACP,求点P的坐标.
3.如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;(2)根据图象,直接写出当x<0时不等式>﹣x+5的解集;
(3)求△AOD的面积.
4.如图,在直角坐标系中,直线y=﹣x与反比例函数y=的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;(2)将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
5.如图,已知A(﹣4,0.5),B(﹣1,2)是一次函数y=ax+b与反比例函数(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
6.如图,一次函数y=﹣x+的图象与反比例函数y=(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.(1)求反比例函数的解析式;(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
7.已知:如图,矩形ABCD中,AB=5,AD=3,E是CD上一点(不与C、D重合),连接AE,过点B作BF⊥AE,垂足为F.
(1)若DE=2,求cos∠ABF的值;
(2)设AE=x,BF=y,①求y关于x之间的函数关系式,写出自变量x的取值范围;②问当点E从D运动到C,BF的值在增大还是减小?并说明理由.
(3)当△AEB为等腰三角形时,求BF的长.
8.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.
(1)求反比例函数y=的表达式;
(2)求点B的坐标及OB所在直线解析式;
(3)求△OAP的面积.
9.如图,在平面直角坐标系xOy中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
10.如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
11.如图,在平面直角坐标系xOy中,一次函数y=﹣x+5的图象与反比例函数y=(k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且△BOC的面积为.
(1)求反比例函数的表达式;
(2)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度?
12.如图,一次函数y=﹣x+b与反比例函数y=﹣(x>0)的图象分别交于点A(﹣2,m),B(4,n),与y轴交于点C,连接OA,OB.
(1)求一次函数y=﹣x+b和反比例函数y=(x>0)的表达式;
(2)求△AOB的面积.
13.如图,在平面直角坐标系xOy中,直角△ABC的顶点A,B在函数y=(k>0,x>0)图象上,AC∥x轴,线段AB的垂直平分线交CB于点M,交AC的延长线于点E,点A纵坐标为2,点B横坐标为1,CE=1.
(1)求点C和点E的坐标及k的值;
(2)连接BE,求△MBE的面积.
14.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象经过点A(2,6),将点A向右平移2个单位,再向下平移a个单位得到点B,点B恰好落在反比例函数y=(x>0)的图象上,过A,B两点的直线与y轴交于点C.
(1)求k的值及点C的坐标;
(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.
15.如图,点A(a,2)在反比例函数y=的图象上,AB∥x轴,且交y轴于点C,交反比例函数y=于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y=的解析式;
(3)点D为反比例函数y=上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
16.如图,在平面直角坐标系xOy中,一次函数y=x+b的图象分别与x轴、y轴交于点A、B,与反比例函数y=(x>0)的图象交于点C,连接OC.已知点A(﹣4,0),AB=2BC.
(1)求b、k的值;
(2)求△AOC的面积.
17.如图,在平面直角坐标系中,一次函数y=x﹣2的图象与y轴相交于点A,与反比例函数y=在第一象限内的图象相交于点B(m,2),过点B作BC⊥y轴于点C.
(1)求反比例函数的解析式;
(2)求△ABC的面积.
18.如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A,B,与反比例函数y2=(m>0)的图象交于点C(1,2),D(2,n).
(1)分别求出两个函数的解析式;
(2)连接OD,求△BOD的面积.
19.如图,已知反比例函数y=(k≠0)与正比例函数y=2x的图象交于A(1,m),B两点.
(1)求该反比例函数的表达式;
(2)若点C在x轴上,且△BOC的面积为3,求点C的坐标.
20.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象交于A(﹣1,n),B(3,﹣2)两点.
(1)求一次函数和反比例函数的解析式;
(2)点P在x轴上,且满足△ABP的面积等于4,请直接写出点P的坐标.
九年级数学反比例函数专题
参考答案与试题解析
1.解:(1)∵OA=OB=OD=2.
∴A点坐标为(﹣2,0),B点坐标为(0,2),
∵OB∥CD,
∴OB:CD=OA:AD,
∴CD==4,
∴C点坐标为(2,4),
(2)把C(2,4)代入,得m=2×4=8,
∴反比例函数的解析式为,
把A(﹣2,0),B(0,2)代入y=kx+b得,
解得,
∴一次函数的解析式为y=x+2.
2.解:(1)∵点B(2,﹣1)在反比例函数y=的图象上,
∴﹣1=,
解得,m=﹣2,
∴反比例函数解析式为:y=﹣,
∵点A(﹣1,n)在反比例函数y=﹣的图象上,
∴n=﹣=2,
∴点A的坐标为(﹣1,2),
则,
解得,,
∴一次函数的解析式为:y=﹣x+1;
(2)对于y=﹣x+1,当x=0时,y=1,
∴点C的坐标为(0,1),
∵点D与点C关于x轴对称,
∴点D的坐标为(0,﹣1),
∴BD∥x轴,且BD=2,
∴S△ABD=×2×3=3,
设点P的坐标为(0,m),
由题意得,×|m﹣1|×1=3,
解得,m=﹣5或7,
∴点P的坐标为(0,﹣5)或(0,7).
3.解:(1)y=﹣x+5,
当y=0时,x=5,
即OC=5,C点的坐标是(5,0),
过A作AM⊥x轴于M,
∵S△AOC=15,
∴=15,
解得:AM=6,
即A点的纵坐标是6,
把y=6代入y=﹣x+5得:x=﹣1,
即A点的坐标是(﹣1,6),
把A点的坐标代入y=得:k=﹣6;
(2)当x<0时不等式>﹣x+5的解集是﹣1<x<0;
(3)∵CD:AC=2:3,
∴CD:AD=2:1,
∵S△AOC=15,
∴△AOD的面积=S△AOC==7.5.
4.解:(1)令一次函数y=﹣x中y=3,则3=﹣x,
解得:x=﹣6,即点A的坐标为(﹣6,3).
∵点A(﹣6,3)在反比例函数y=的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣;
(2)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为48,
∴S△ABF=OF (xB﹣xA)=48,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴b×12=48,
∴b=8.
∴平移后的直线的函数表达式为y=﹣x+8.
5.解:(1)当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(2)把A(﹣4,0.5),B(﹣1,2)代入y=kx+b得,
,解得,
所以一次函数解析式为y=x+;
把B(﹣1,2)代入,得m=﹣1×2=﹣2;
(3)连接PC、PD,如图,设P点坐标为(t,t+).
∵△PCA和△PDB面积相等,
∴ (t+4)= 1 (2﹣t﹣),
解得t=﹣,
∴P点坐标为(﹣,).
6.解:(1)∵反比例函数y=(k>0)的图象过点A,过A点作x轴的垂线,垂足为M,△AOM面积为1,
∴|k|=1,
∵k>0,
∴k=2,
故反比例函数的解析式为:y=;
(2)作点A关于y轴的对称点A′,连接A′B,交y轴于点P,则PA+PB最小.
由,解得,或,
∴A(1,2),B(4,),
∴A′(﹣1,2),最小值A′B==.
设直线A′B的解析式为y=mx+n,
则,解得,
∴直线A′B的解析式为y=﹣x+,
∴x=0时,y=,
∴P点坐标为(0,).
7.解:(1)∵BF⊥AE,
∴∠FBA+∠FAB=90°,∠AFB=90°,
∵∠D=∠AFB=90°,
∵∠DAE+∠EAB=90°,
∴∠FBA=∠EAD,
∴△ABF∽△EDA
∵DE=2,AD=3,
∴AE=,
∴cos∠ABF===;
(2)根据(1)可知:
①=即y=;
②减小,因为y=中,每个象限内,y随x的增大而减小;
(3)当△AEB为等腰三角形时,有3种情况:
a、当AB=BE时,则BE=5,则CE==4,∴DE=5﹣4=1,
∴AE==,
∴AF=,
∴BF=;
b、当AE=BE时,E为CD中点,则DE=2.5,AE=,
∵AD AB=BF AE,
∴3×5=BF×,
∴BF=;
c、当AB=AE=5时,△ABF≌△AED,则BF=AD=3.
所以BF的值为:或 或3.
8.解:(1)将点A(4,3)代入y=(k≠0),
得:k=12,
则反比例函数解析式为y=;
(2)如图,过点A作AC⊥x轴于点C,
则OC=4、AC=3,
∴OA==5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
设OB所在直线解析式为y=mx(m≠0),
将点B(9,3)代入得m=,
∴OB所在直线解析式为y=x;
(3)联立解析式:
解得:,
可得点P坐标为(6,2),
过点P作PD⊥x轴,延长DP交AB于点E,连接AP,
则点E坐标为(6,3),
∴AE=2,PE=1,PD=2,
则△OAP的面积=×(2+6)×3﹣×6×2﹣×2×1=5.
8.解:(1)由得,
∴A(﹣2,4),
∵反比例函数y=的图象经过点A,
∴k=﹣2×4=﹣8,
∴反比例函数的表达式是y=﹣;
(2)解得或,
∴B(﹣8,1),
由直线AB的解析式为y=x+5得到直线与x轴的交点为(﹣10,0),
∴S△AOB=×10×4﹣×10×1=15.
9.解:(1)联立y=x+5①和y=﹣2x得:,
解得:,故点A(﹣2,4),
将点A的坐标代入反比例函数表达式得:4=,解得:k=﹣8,
故反比例函数表达式为:y=﹣②;
(2)联立①②并解得:x=﹣2或﹣8,
当x=﹣8时,y=x+5=1,故点B(﹣8,1),
设y=x+5交x轴于点C,
令y=0,则x+5=0,
∴x=﹣10,
∴C(﹣10,0),
过点A、B分别作x轴的垂线交x轴于点M、N,
则S△AOB=S△AOC﹣S△BOC=OC AMOC BN=.
10.解:(1)一次函数y=﹣x+5中,令y=0,解得x=5,
∴C(5,0),
∴OC=5,
作BD⊥OC于D,
∵△BOC的面积为,
∴OC BD=,即BD=,
∴BD=1,
∴点B的纵坐标为1,
代入y=﹣x+5中,求得x=4,
∴B(4,1),
∵反比例函数y=(k>0)的图象经过B点,
∴k=4×1=4,
∴反比例函数的解析式为y=;
(2)将直线AB向下平移m(m>0)个单位长度得直线解析式为y=﹣x+5﹣m,
∵直线AB向下平移m(m>0)个单位长度后与反比例函数的图象只有一个公共交点,
∴=﹣x+5﹣m,
整理得x2+(m﹣5)x+4=0,
△=(m﹣5)2﹣4×1×4=0,解得m=9或m=1,
即m的值为1或9.
11.解:(1)∵点A在反比例函数y=上,
∴﹣2m=﹣10,
解得m=5,
∴点A坐标为(﹣2,5).
把(﹣2,5)代入y=﹣x+b得5=1+b,
解得b=4,
∴一次函数表达式为y=x+4,
把B(4,n)代入y=x+4得n=﹣2+4=2,
∴点B坐标为(4,2),
∵点B在反比例函数y=图象上,
∴k=4×2=8,
∴反比例函数表达式为y=.
(2)把x=0代入y=x+4得y=4,
∴点C坐标为(0,4),
∴S△AOB=S△AOC+S△BOC=×4×2+×4×4=12.
12.解:(1)由题意得点A的坐标为(,2),点B的坐标为(1,k),
又AC∥x轴,且△ACB为直角三角形,
∴点C的坐标为(1,2),
又CE=1,
∴点E的坐标为(2,2),
∵点E在线段AB的垂直平分线上,
∴EA=EB,
在Rt△BCE中,EB2=BC2+CE2,
∴1+(k﹣2)2=,
∴k=2或,
当k=2时,点A,B,C三点重合,不能构成三角形,故舍去,
∴k=,
∴C(1,2),E(2,2),k=;
(2)由(1)可得,AC=,BC=,CE=1,
设AB的中点为D,
AB==,BD==,
∵∠ABC=∠MBD,∠BDM=∠BCA=90°,
∴△BDM∽△BCA,
∴=,
∴BM=×=,
∴S△MBE==×1=.
13.解:(1)把点A(2,6)代入y=,k=2×6=12,
∴反比例函数的解析式为y=,
∵将点A向右平移2个单位,
∴x=4,
当x=4时,y==3,
∴B(4,3),
设直线AB的解析式为y=mx+n,
由题意可得,
解得,
∴y=﹣x+9,
当x=0时,y=9,
∴C(0,9);
(2)由(1)知CD=9﹣5=4,
∴S△ABD=S△BCD﹣S△ACD=CD |xB|﹣CD |xA|=×4×4﹣×4×2=4.
14.解:(1)∵点A(a,2)在反比例函数y=的图象上,
∴2=,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y=得:2=,
∴k=﹣2,
∴反比例函数y=的解析式为y=;
(3)设D(t,),而A(2,2),
∴AD中点E(,+1),
而E在y轴上,
∴=0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOE=OE |xD|=××2=,
S△AOE=OE |xA|=××2=,
∴△OAD面积S=S△DOE+S△AOE=3.
15.解:(1)作CD⊥y轴于D,
则△ABO∽△CBD,
∴,
∵AB=2BC,
∴AO=2CD,
∵点A(﹣4,0),
∴OA=4,
∴CD=2,
∵点A(﹣4,0)在一次函数y=x+b的图象上,
∴b=2,
∴,
当x=2时,y=3,
∴C(2,3),
∵点C在反比例函数y=(x>0)的图象上,
∴k=2×3=6;
(2)作CE⊥x轴于E,
S△AOC=.
16.解:(1)∵B点是直线与反比例函数交点,
∴B点坐标满足一次函数解析式,
∴,
∴m=3,
∴B(3,2),
∴k=6,
∴反比例函数的解析式为;
(2)∵BC⊥y轴,
∴C(0,2),BC∥x轴,
∴BC=3,
令x=0,则y=,
∴A(0,﹣2),
∴AC=4,
∴,
∴△ABC的面积为6.
17.解:(1)由y2=过点C(1,2)和D(2,n)可得:
,
解得:,
故y2=,
又由y1=kx+b过点C(1,2)和D(2,1)可得:
,
解得,
故y1=﹣x+3.
(2)由y1=﹣x+3过点B,可知B(0,3),
故OB=3,
而点D到y轴的距离为2,
∴S△BOD==3.
18.解:(1)把A(1,m)代入y=2x中,
得m=2,
∴点A的坐标为(1,2),
把点A(1,2)代入y=中,
得k=2,
∴反比例函数的解析式为y=;
(2)过点B作BD垂直与x轴,垂足为D,
设点C的坐标为(a,0),
∵点A与点B关于原点对称,
∴点B的坐标为(﹣1,﹣2),
∴BD=|﹣2|=2,OC=|a|,
S△BOC==,
解得:a=3或a=﹣3,
∴点C的坐标为(3,0)或(﹣3,0).
19.解:(1)由题意可得:
点B(3,﹣2)在反比例函数图象上,
∴,则m=﹣6,
∴反比例函数的解析式为,
将A(﹣1,n)代入,
得:,即A(﹣1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为y1=﹣2x+4;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为y1=﹣2x+4,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
|a﹣2|=4,即|a﹣2|=4,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
第1页(共1页)
求三角形面积问题
方法:水平宽铅垂高÷2
()
注:水平宽铅垂高求面积的方法本质上属于分割的方法。
【练习】
1.如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=的图象在第一象限内的部分交于点C,CD垂直于x轴,垂足为D,其中OA=OB=OD=2.
(1)求一次函数和反比例函数的解析式.
(2)若点P在y轴上,且,求点P的坐标。
2.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)当时,直接写出自变量x的取值范围。
(3)若点D与点C关于x轴对称,点P为y轴上一点,且S△ABD=S△ACP,求点P的坐标.
3.如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;(2)根据图象,直接写出当x<0时不等式>﹣x+5的解集;
(3)求△AOD的面积.
4.如图,在直角坐标系中,直线y=﹣x与反比例函数y=的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;(2)将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
5.如图,已知A(﹣4,0.5),B(﹣1,2)是一次函数y=ax+b与反比例函数(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
6.如图,一次函数y=﹣x+的图象与反比例函数y=(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.(1)求反比例函数的解析式;(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
7.已知:如图,矩形ABCD中,AB=5,AD=3,E是CD上一点(不与C、D重合),连接AE,过点B作BF⊥AE,垂足为F.
(1)若DE=2,求cos∠ABF的值;
(2)设AE=x,BF=y,①求y关于x之间的函数关系式,写出自变量x的取值范围;②问当点E从D运动到C,BF的值在增大还是减小?并说明理由.
(3)当△AEB为等腰三角形时,求BF的长.
8.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.
(1)求反比例函数y=的表达式;
(2)求点B的坐标及OB所在直线解析式;
(3)求△OAP的面积.
9.如图,在平面直角坐标系xOy中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
10.如图,在平面直角坐标系中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)求反比例函数的表达式;
(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
11.如图,在平面直角坐标系xOy中,一次函数y=﹣x+5的图象与反比例函数y=(k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且△BOC的面积为.
(1)求反比例函数的表达式;
(2)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度?
12.如图,一次函数y=﹣x+b与反比例函数y=﹣(x>0)的图象分别交于点A(﹣2,m),B(4,n),与y轴交于点C,连接OA,OB.
(1)求一次函数y=﹣x+b和反比例函数y=(x>0)的表达式;
(2)求△AOB的面积.
13.如图,在平面直角坐标系xOy中,直角△ABC的顶点A,B在函数y=(k>0,x>0)图象上,AC∥x轴,线段AB的垂直平分线交CB于点M,交AC的延长线于点E,点A纵坐标为2,点B横坐标为1,CE=1.
(1)求点C和点E的坐标及k的值;
(2)连接BE,求△MBE的面积.
14.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象经过点A(2,6),将点A向右平移2个单位,再向下平移a个单位得到点B,点B恰好落在反比例函数y=(x>0)的图象上,过A,B两点的直线与y轴交于点C.
(1)求k的值及点C的坐标;
(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.
15.如图,点A(a,2)在反比例函数y=的图象上,AB∥x轴,且交y轴于点C,交反比例函数y=于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y=的解析式;
(3)点D为反比例函数y=上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
16.如图,在平面直角坐标系xOy中,一次函数y=x+b的图象分别与x轴、y轴交于点A、B,与反比例函数y=(x>0)的图象交于点C,连接OC.已知点A(﹣4,0),AB=2BC.
(1)求b、k的值;
(2)求△AOC的面积.
17.如图,在平面直角坐标系中,一次函数y=x﹣2的图象与y轴相交于点A,与反比例函数y=在第一象限内的图象相交于点B(m,2),过点B作BC⊥y轴于点C.
(1)求反比例函数的解析式;
(2)求△ABC的面积.
18.如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A,B,与反比例函数y2=(m>0)的图象交于点C(1,2),D(2,n).
(1)分别求出两个函数的解析式;
(2)连接OD,求△BOD的面积.
19.如图,已知反比例函数y=(k≠0)与正比例函数y=2x的图象交于A(1,m),B两点.
(1)求该反比例函数的表达式;
(2)若点C在x轴上,且△BOC的面积为3,求点C的坐标.
20.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0)的图象交于A(﹣1,n),B(3,﹣2)两点.
(1)求一次函数和反比例函数的解析式;
(2)点P在x轴上,且满足△ABP的面积等于4,请直接写出点P的坐标.
九年级数学反比例函数专题
参考答案与试题解析
1.解:(1)∵OA=OB=OD=2.
∴A点坐标为(﹣2,0),B点坐标为(0,2),
∵OB∥CD,
∴OB:CD=OA:AD,
∴CD==4,
∴C点坐标为(2,4),
(2)把C(2,4)代入,得m=2×4=8,
∴反比例函数的解析式为,
把A(﹣2,0),B(0,2)代入y=kx+b得,
解得,
∴一次函数的解析式为y=x+2.
2.解:(1)∵点B(2,﹣1)在反比例函数y=的图象上,
∴﹣1=,
解得,m=﹣2,
∴反比例函数解析式为:y=﹣,
∵点A(﹣1,n)在反比例函数y=﹣的图象上,
∴n=﹣=2,
∴点A的坐标为(﹣1,2),
则,
解得,,
∴一次函数的解析式为:y=﹣x+1;
(2)对于y=﹣x+1,当x=0时,y=1,
∴点C的坐标为(0,1),
∵点D与点C关于x轴对称,
∴点D的坐标为(0,﹣1),
∴BD∥x轴,且BD=2,
∴S△ABD=×2×3=3,
设点P的坐标为(0,m),
由题意得,×|m﹣1|×1=3,
解得,m=﹣5或7,
∴点P的坐标为(0,﹣5)或(0,7).
3.解:(1)y=﹣x+5,
当y=0时,x=5,
即OC=5,C点的坐标是(5,0),
过A作AM⊥x轴于M,
∵S△AOC=15,
∴=15,
解得:AM=6,
即A点的纵坐标是6,
把y=6代入y=﹣x+5得:x=﹣1,
即A点的坐标是(﹣1,6),
把A点的坐标代入y=得:k=﹣6;
(2)当x<0时不等式>﹣x+5的解集是﹣1<x<0;
(3)∵CD:AC=2:3,
∴CD:AD=2:1,
∵S△AOC=15,
∴△AOD的面积=S△AOC==7.5.
4.解:(1)令一次函数y=﹣x中y=3,则3=﹣x,
解得:x=﹣6,即点A的坐标为(﹣6,3).
∵点A(﹣6,3)在反比例函数y=的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣;
(2)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为48,
∴S△ABF=OF (xB﹣xA)=48,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴b×12=48,
∴b=8.
∴平移后的直线的函数表达式为y=﹣x+8.
5.解:(1)当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(2)把A(﹣4,0.5),B(﹣1,2)代入y=kx+b得,
,解得,
所以一次函数解析式为y=x+;
把B(﹣1,2)代入,得m=﹣1×2=﹣2;
(3)连接PC、PD,如图,设P点坐标为(t,t+).
∵△PCA和△PDB面积相等,
∴ (t+4)= 1 (2﹣t﹣),
解得t=﹣,
∴P点坐标为(﹣,).
6.解:(1)∵反比例函数y=(k>0)的图象过点A,过A点作x轴的垂线,垂足为M,△AOM面积为1,
∴|k|=1,
∵k>0,
∴k=2,
故反比例函数的解析式为:y=;
(2)作点A关于y轴的对称点A′,连接A′B,交y轴于点P,则PA+PB最小.
由,解得,或,
∴A(1,2),B(4,),
∴A′(﹣1,2),最小值A′B==.
设直线A′B的解析式为y=mx+n,
则,解得,
∴直线A′B的解析式为y=﹣x+,
∴x=0时,y=,
∴P点坐标为(0,).
7.解:(1)∵BF⊥AE,
∴∠FBA+∠FAB=90°,∠AFB=90°,
∵∠D=∠AFB=90°,
∵∠DAE+∠EAB=90°,
∴∠FBA=∠EAD,
∴△ABF∽△EDA
∵DE=2,AD=3,
∴AE=,
∴cos∠ABF===;
(2)根据(1)可知:
①=即y=;
②减小,因为y=中,每个象限内,y随x的增大而减小;
(3)当△AEB为等腰三角形时,有3种情况:
a、当AB=BE时,则BE=5,则CE==4,∴DE=5﹣4=1,
∴AE==,
∴AF=,
∴BF=;
b、当AE=BE时,E为CD中点,则DE=2.5,AE=,
∵AD AB=BF AE,
∴3×5=BF×,
∴BF=;
c、当AB=AE=5时,△ABF≌△AED,则BF=AD=3.
所以BF的值为:或 或3.
8.解:(1)将点A(4,3)代入y=(k≠0),
得:k=12,
则反比例函数解析式为y=;
(2)如图,过点A作AC⊥x轴于点C,
则OC=4、AC=3,
∴OA==5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
设OB所在直线解析式为y=mx(m≠0),
将点B(9,3)代入得m=,
∴OB所在直线解析式为y=x;
(3)联立解析式:
解得:,
可得点P坐标为(6,2),
过点P作PD⊥x轴,延长DP交AB于点E,连接AP,
则点E坐标为(6,3),
∴AE=2,PE=1,PD=2,
则△OAP的面积=×(2+6)×3﹣×6×2﹣×2×1=5.
8.解:(1)由得,
∴A(﹣2,4),
∵反比例函数y=的图象经过点A,
∴k=﹣2×4=﹣8,
∴反比例函数的表达式是y=﹣;
(2)解得或,
∴B(﹣8,1),
由直线AB的解析式为y=x+5得到直线与x轴的交点为(﹣10,0),
∴S△AOB=×10×4﹣×10×1=15.
9.解:(1)联立y=x+5①和y=﹣2x得:,
解得:,故点A(﹣2,4),
将点A的坐标代入反比例函数表达式得:4=,解得:k=﹣8,
故反比例函数表达式为:y=﹣②;
(2)联立①②并解得:x=﹣2或﹣8,
当x=﹣8时,y=x+5=1,故点B(﹣8,1),
设y=x+5交x轴于点C,
令y=0,则x+5=0,
∴x=﹣10,
∴C(﹣10,0),
过点A、B分别作x轴的垂线交x轴于点M、N,
则S△AOB=S△AOC﹣S△BOC=OC AMOC BN=.
10.解:(1)一次函数y=﹣x+5中,令y=0,解得x=5,
∴C(5,0),
∴OC=5,
作BD⊥OC于D,
∵△BOC的面积为,
∴OC BD=,即BD=,
∴BD=1,
∴点B的纵坐标为1,
代入y=﹣x+5中,求得x=4,
∴B(4,1),
∵反比例函数y=(k>0)的图象经过B点,
∴k=4×1=4,
∴反比例函数的解析式为y=;
(2)将直线AB向下平移m(m>0)个单位长度得直线解析式为y=﹣x+5﹣m,
∵直线AB向下平移m(m>0)个单位长度后与反比例函数的图象只有一个公共交点,
∴=﹣x+5﹣m,
整理得x2+(m﹣5)x+4=0,
△=(m﹣5)2﹣4×1×4=0,解得m=9或m=1,
即m的值为1或9.
11.解:(1)∵点A在反比例函数y=上,
∴﹣2m=﹣10,
解得m=5,
∴点A坐标为(﹣2,5).
把(﹣2,5)代入y=﹣x+b得5=1+b,
解得b=4,
∴一次函数表达式为y=x+4,
把B(4,n)代入y=x+4得n=﹣2+4=2,
∴点B坐标为(4,2),
∵点B在反比例函数y=图象上,
∴k=4×2=8,
∴反比例函数表达式为y=.
(2)把x=0代入y=x+4得y=4,
∴点C坐标为(0,4),
∴S△AOB=S△AOC+S△BOC=×4×2+×4×4=12.
12.解:(1)由题意得点A的坐标为(,2),点B的坐标为(1,k),
又AC∥x轴,且△ACB为直角三角形,
∴点C的坐标为(1,2),
又CE=1,
∴点E的坐标为(2,2),
∵点E在线段AB的垂直平分线上,
∴EA=EB,
在Rt△BCE中,EB2=BC2+CE2,
∴1+(k﹣2)2=,
∴k=2或,
当k=2时,点A,B,C三点重合,不能构成三角形,故舍去,
∴k=,
∴C(1,2),E(2,2),k=;
(2)由(1)可得,AC=,BC=,CE=1,
设AB的中点为D,
AB==,BD==,
∵∠ABC=∠MBD,∠BDM=∠BCA=90°,
∴△BDM∽△BCA,
∴=,
∴BM=×=,
∴S△MBE==×1=.
13.解:(1)把点A(2,6)代入y=,k=2×6=12,
∴反比例函数的解析式为y=,
∵将点A向右平移2个单位,
∴x=4,
当x=4时,y==3,
∴B(4,3),
设直线AB的解析式为y=mx+n,
由题意可得,
解得,
∴y=﹣x+9,
当x=0时,y=9,
∴C(0,9);
(2)由(1)知CD=9﹣5=4,
∴S△ABD=S△BCD﹣S△ACD=CD |xB|﹣CD |xA|=×4×4﹣×4×2=4.
14.解:(1)∵点A(a,2)在反比例函数y=的图象上,
∴2=,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y=得:2=,
∴k=﹣2,
∴反比例函数y=的解析式为y=;
(3)设D(t,),而A(2,2),
∴AD中点E(,+1),
而E在y轴上,
∴=0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOE=OE |xD|=××2=,
S△AOE=OE |xA|=××2=,
∴△OAD面积S=S△DOE+S△AOE=3.
15.解:(1)作CD⊥y轴于D,
则△ABO∽△CBD,
∴,
∵AB=2BC,
∴AO=2CD,
∵点A(﹣4,0),
∴OA=4,
∴CD=2,
∵点A(﹣4,0)在一次函数y=x+b的图象上,
∴b=2,
∴,
当x=2时,y=3,
∴C(2,3),
∵点C在反比例函数y=(x>0)的图象上,
∴k=2×3=6;
(2)作CE⊥x轴于E,
S△AOC=.
16.解:(1)∵B点是直线与反比例函数交点,
∴B点坐标满足一次函数解析式,
∴,
∴m=3,
∴B(3,2),
∴k=6,
∴反比例函数的解析式为;
(2)∵BC⊥y轴,
∴C(0,2),BC∥x轴,
∴BC=3,
令x=0,则y=,
∴A(0,﹣2),
∴AC=4,
∴,
∴△ABC的面积为6.
17.解:(1)由y2=过点C(1,2)和D(2,n)可得:
,
解得:,
故y2=,
又由y1=kx+b过点C(1,2)和D(2,1)可得:
,
解得,
故y1=﹣x+3.
(2)由y1=﹣x+3过点B,可知B(0,3),
故OB=3,
而点D到y轴的距离为2,
∴S△BOD==3.
18.解:(1)把A(1,m)代入y=2x中,
得m=2,
∴点A的坐标为(1,2),
把点A(1,2)代入y=中,
得k=2,
∴反比例函数的解析式为y=;
(2)过点B作BD垂直与x轴,垂足为D,
设点C的坐标为(a,0),
∵点A与点B关于原点对称,
∴点B的坐标为(﹣1,﹣2),
∴BD=|﹣2|=2,OC=|a|,
S△BOC==,
解得:a=3或a=﹣3,
∴点C的坐标为(3,0)或(﹣3,0).
19.解:(1)由题意可得:
点B(3,﹣2)在反比例函数图象上,
∴,则m=﹣6,
∴反比例函数的解析式为,
将A(﹣1,n)代入,
得:,即A(﹣1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为y1=﹣2x+4;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为y1=﹣2x+4,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
|a﹣2|=4,即|a﹣2|=4,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
第1页(共1页)
