2021-2022学年湘教版九年级数学下册第3章 投影与视图 单元测试(Word版含简答)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册第3章 投影与视图 单元测试(Word版含简答) | 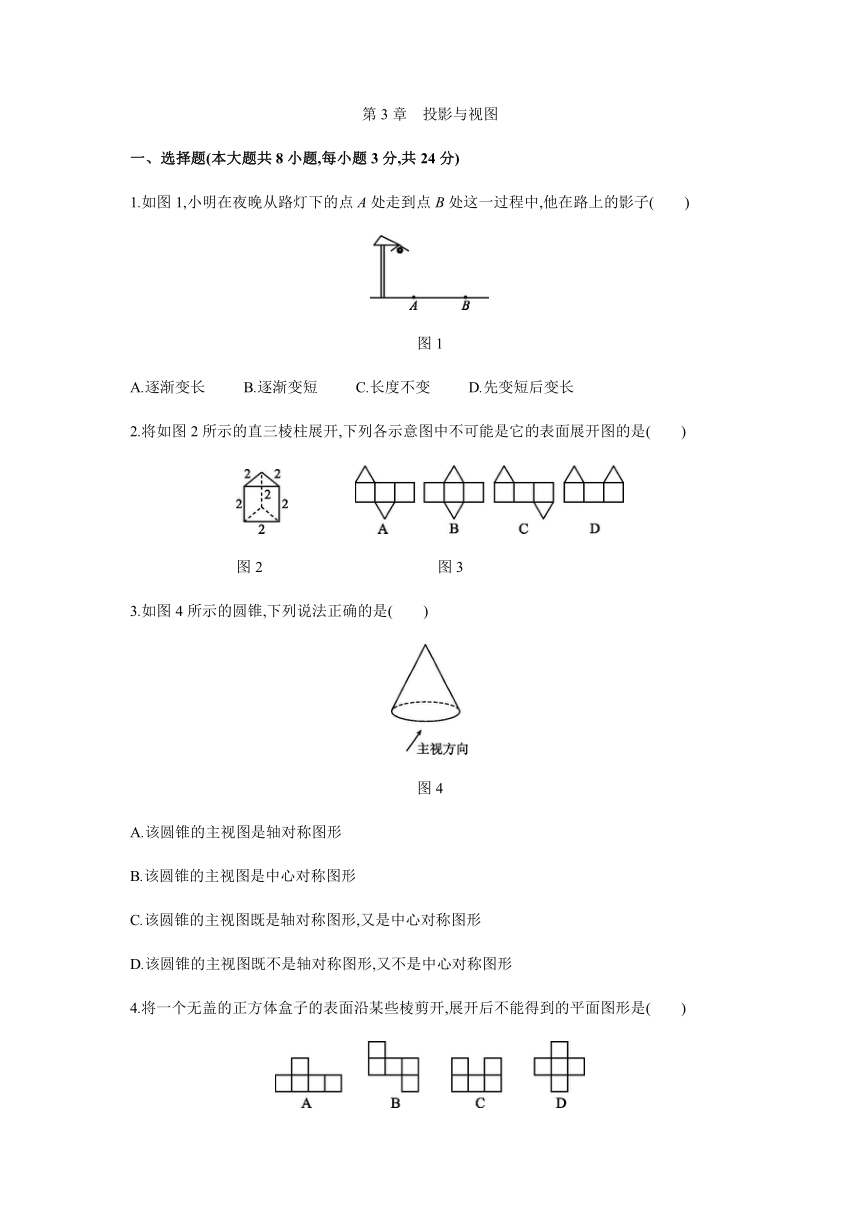 | |
| 格式 | docx | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 16:26:55 | ||
图片预览


文档简介
第3章 投影与视图
一、选择题(本大题共8小题,每小题3分,共24分)
1.如图1,小明在夜晚从路灯下的点A处走到点B处这一过程中,他在路上的影子( )
图1
A.逐渐变长 B.逐渐变短 C.长度不变 D.先变短后变长
2.将如图2所示的直三棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
图2 图3
3.如图4所示的圆锥,下列说法正确的是( )
图4
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
4.将一个无盖的正方体盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )
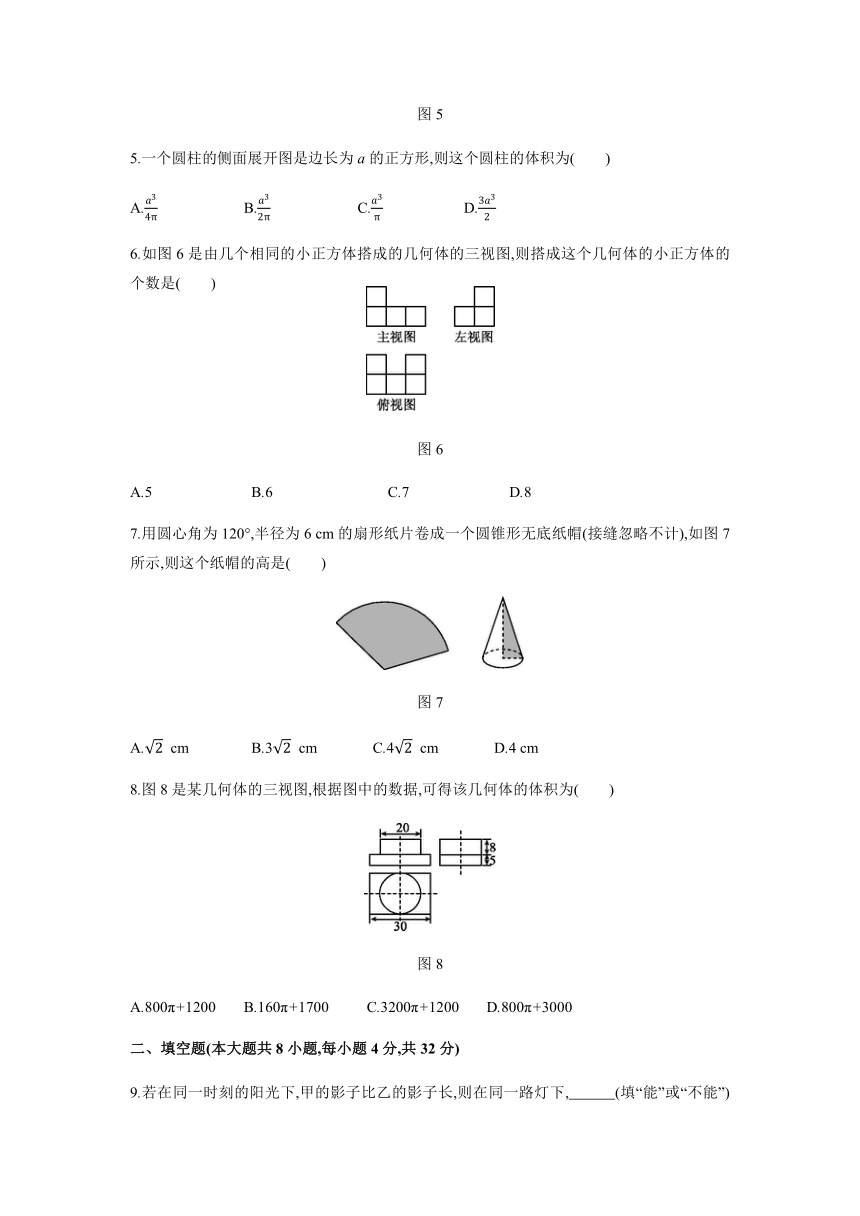
图5
5.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
6.如图6是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
图6
A.5 B.6 C.7 D.8
7.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),如图7所示,则这个纸帽的高是( )
图7
A. cm B.3 cm C.4 cm D.4 cm
8.图8是某几何体的三视图,根据图中的数据,可得该几何体的体积为( )
图8
A.800π+1200 B.160π+1700 C.3200π+1200 D.800π+3000
二、填空题(本大题共8小题,每小题4分,共32分)
9.若在同一时刻的阳光下,甲的影子比乙的影子长,则在同一路灯下, (填“能”或“不能”)判断甲、乙谁的影子长.
10.在长方体、圆柱、圆锥、球体中,三视图均一样的几何体是 .
11.如图9所示的几何体中,主视图与左视图都是长方形的是 (填序号).
图9
12.三棱柱的底面边长都是3 cm,侧棱长为5 cm,则它的侧面展开图的面积为 cm2.
13.如图10,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是 .
图10
14.若一个几何体的三视图如图11所示,则这个几何体的名称是 .
图11
15.图12是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 .
图12
16.在桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图13所示,设组成这个几何体的小正方体的个数为n,则n的最小值为 .
图13
三、解答题(共44分)
17.(10分)在同一时刻、同一地点,一棵树(EF)和一旗杆(DC)的影子如图14所示.
(1)该投影是平行投影还是中心投影 (2)画出小明的影子.
图14
18.(10分)如图15是一个几何体的三视图(单位:cm).
(1)说出组成该几何体的两部分分别是什么几何体;
(2)求该几何体的体积(结果保留π).
图15
19.(12分)如图16所示,正方体盒子的棱长为2,BC的中点为M.
(1)一只蚂蚁从点M沿正方体的棱爬行到点D1,蚂蚁爬行的最短路程是多少
(2)若蚂蚁从点M沿正方体的表面爬行到点D1,请你结合正方体的展开图画出蚂蚁爬行的最短路线.
图16
20.(12分)如图17,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子,已知窗框的影子DE到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口(即AB)的高度.
图17
答案
1.A 2.D 3.A 4.C 5.A 6.B7.C 8.D
9.不能
10.球体
11.(1)(3)(4) 12.45 13.7 14.直四棱柱
15.72 16.5
17.解:(1)中心投影. (2)略.
18.解:(1)上部分是圆柱,下部分是长方体.
(2)该几何体的体积=30×40×25+π×(20÷2)2×32=(30000+3200π)cm3.
19.解:(1)一只蚂蚁从点M沿正方体的棱爬到点D1,蚂蚁爬行的最短路程是1+2+2=5.
(2)当把正方体的面B1BCC1展开到和面C1CDD1在同一平面上时,得到的图形如图所示,图中的线段MD1表示蚂蚁爬行的最短路线(也可将其他面展开).
20.解:由于阳光是平行光线,即AE∥BD,
∴∠AEC=∠BDC.
又∵∠BCD是公共角,
∴△AEC∽△BDC,
∴=.
又∵AC=AB+BC,DC=EC-DE,EC=3.9 m,DE=2.1 m,BC=1.2 m,
∴=,解得AB=1.4(m).
答:窗口的高度为1.4 m.
一、选择题(本大题共8小题,每小题3分,共24分)
1.如图1,小明在夜晚从路灯下的点A处走到点B处这一过程中,他在路上的影子( )
图1
A.逐渐变长 B.逐渐变短 C.长度不变 D.先变短后变长
2.将如图2所示的直三棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
图2 图3
3.如图4所示的圆锥,下列说法正确的是( )
图4
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
4.将一个无盖的正方体盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )
图5
5.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
6.如图6是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
图6
A.5 B.6 C.7 D.8
7.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),如图7所示,则这个纸帽的高是( )
图7
A. cm B.3 cm C.4 cm D.4 cm
8.图8是某几何体的三视图,根据图中的数据,可得该几何体的体积为( )
图8
A.800π+1200 B.160π+1700 C.3200π+1200 D.800π+3000
二、填空题(本大题共8小题,每小题4分,共32分)
9.若在同一时刻的阳光下,甲的影子比乙的影子长,则在同一路灯下, (填“能”或“不能”)判断甲、乙谁的影子长.
10.在长方体、圆柱、圆锥、球体中,三视图均一样的几何体是 .
11.如图9所示的几何体中,主视图与左视图都是长方形的是 (填序号).
图9
12.三棱柱的底面边长都是3 cm,侧棱长为5 cm,则它的侧面展开图的面积为 cm2.
13.如图10,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是 .
图10
14.若一个几何体的三视图如图11所示,则这个几何体的名称是 .
图11
15.图12是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 .
图12
16.在桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图13所示,设组成这个几何体的小正方体的个数为n,则n的最小值为 .
图13
三、解答题(共44分)
17.(10分)在同一时刻、同一地点,一棵树(EF)和一旗杆(DC)的影子如图14所示.
(1)该投影是平行投影还是中心投影 (2)画出小明的影子.
图14
18.(10分)如图15是一个几何体的三视图(单位:cm).
(1)说出组成该几何体的两部分分别是什么几何体;
(2)求该几何体的体积(结果保留π).
图15
19.(12分)如图16所示,正方体盒子的棱长为2,BC的中点为M.
(1)一只蚂蚁从点M沿正方体的棱爬行到点D1,蚂蚁爬行的最短路程是多少
(2)若蚂蚁从点M沿正方体的表面爬行到点D1,请你结合正方体的展开图画出蚂蚁爬行的最短路线.
图16
20.(12分)如图17,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子,已知窗框的影子DE到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口(即AB)的高度.
图17
答案
1.A 2.D 3.A 4.C 5.A 6.B7.C 8.D
9.不能
10.球体
11.(1)(3)(4) 12.45 13.7 14.直四棱柱
15.72 16.5
17.解:(1)中心投影. (2)略.
18.解:(1)上部分是圆柱,下部分是长方体.
(2)该几何体的体积=30×40×25+π×(20÷2)2×32=(30000+3200π)cm3.
19.解:(1)一只蚂蚁从点M沿正方体的棱爬到点D1,蚂蚁爬行的最短路程是1+2+2=5.
(2)当把正方体的面B1BCC1展开到和面C1CDD1在同一平面上时,得到的图形如图所示,图中的线段MD1表示蚂蚁爬行的最短路线(也可将其他面展开).
20.解:由于阳光是平行光线,即AE∥BD,
∴∠AEC=∠BDC.
又∵∠BCD是公共角,
∴△AEC∽△BDC,
∴=.
又∵AC=AB+BC,DC=EC-DE,EC=3.9 m,DE=2.1 m,BC=1.2 m,
∴=,解得AB=1.4(m).
答:窗口的高度为1.4 m.
