4.4约分(课件)-2021-2022学年数学五年级下册 (21张PPT)
文档属性
| 名称 | 4.4约分(课件)-2021-2022学年数学五年级下册 (21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 593.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 19:34:12 | ||
图片预览






文档简介
(共21张PPT)
约 分
进一步理解分数的基本性质。
能应用分数的基本性质把一个分数化成最简分数。
1.填一填。
3
1
=
6
( )
4
1
=
( )
5
20
4
=
=
20÷ ( )
4÷ ( )
( )
1
20
4
4
5
2
10
3
=
=
10×( )
3 × ( )
( )
30
3
3
9
2.判断每组的两个分数是否相等,并说明理由。
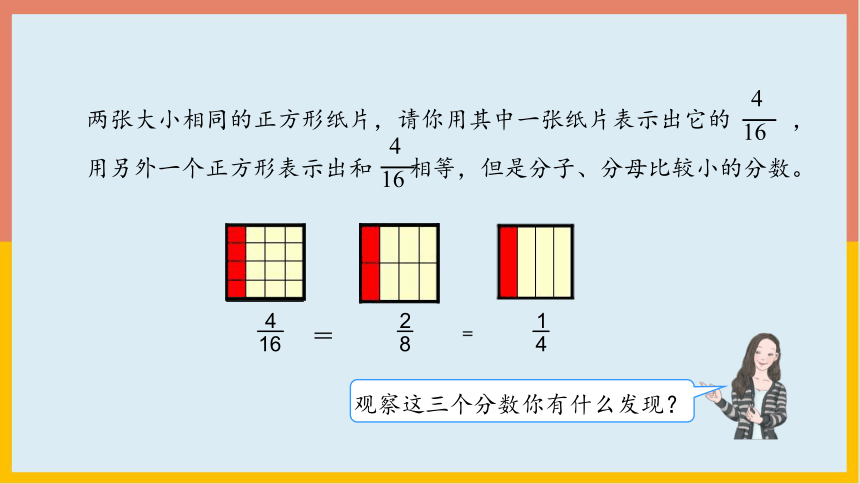
观察这三个分数你有什么发现?
=
﹦
两张大小相同的正方形纸片,请你用其中一张纸片表示出它的 ,
用另外一个正方形表示出和 相等,但是分子、分母比较小的分数。
16
4
16
4
﹦
﹦
﹦
﹦
﹦
﹦
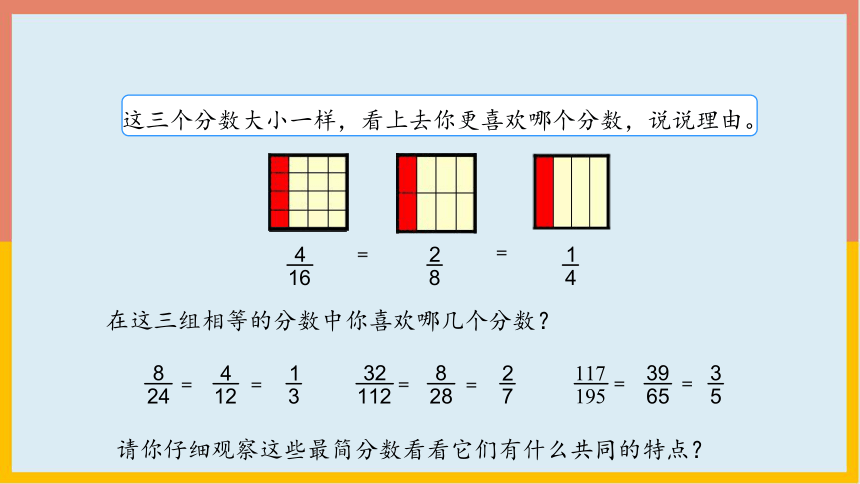
在这三组相等的分数中你喜欢哪几个分数?
请你仔细观察这些最简分数看看它们有什么共同的特点?
﹦
﹦
这三个分数大小一样,看上去你更喜欢哪个分数,说说理由。
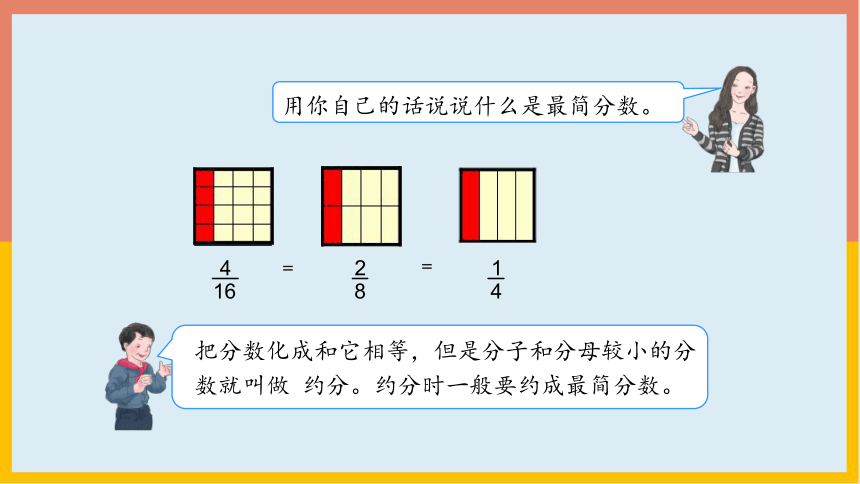
用你自己的话说说什么是最简分数。
把分数化成和它相等,但是分子和分母较小的分数就叫做 约分。约分时一般要约成最简分数。
﹦
﹦
如果没有纸片帮忙,你能把这个分数约分吗?
可以用分子和分母的公因数(1除外)去除。
﹦
16
4
16÷2
4÷2
﹦
﹦
8
2
8÷2
2÷2
﹦
4
1
自己独立想一想,把 约分成一个最简分数。
分步约分:
﹦
30
24
30÷6
24÷6
﹦
5
4
﹦
30
24
30÷2
24÷2
﹦
﹦
15
12
15÷3
12÷3
﹦
5
4
用24和30的最大公因数是6约分。
两种约分的方法都对吗?它们有什么相同的地方呢?
方法一是:一步一步进行约分,每一步都是分子和分母同时除以它们的公因数。
逐次除以大于1的公因数,最后得到最简分数的方法叫做“逐次约分法”。
一次除以最大公因数直接得到最简分数的方法叫做“一次约分法”。
方法二是:一次约分成最简分数,是分子和分母同时除以它们的最大公因数。
这两种约分方法都应用了分数的基本性质,它们有什么不同之处吗?
或者
30
24
12
15
4
5
=
5
4
30
24
5
4
5
4
=
约分过程还可以这样写,在约分的过程中划右斜线,所 得的商分别写在分母的正下方和分子的正上方。
1.请你用喜欢的方式约分 和 。
60
15
75
25
60
15
5
20
1
4
=
4
1
75
25
5
15
1
3
=
3
1
9
2. 下列分数中哪些是最简分数,把不是最简分数的化成最简分数。
5
4
4
3
1
4
5
3. 把上下两行相等的两个分数用线连起来。
4.红色部分和黄色部分哪个多些?为什么?
一样大,因为两个部分都占整个圆的 。
5.观察下面的每个分数的分子和分母,哪些有公因数2?哪些有公因数5?哪些有公因数3?
2
3、5
3
3、5
2、5
2、3
6.把下面分数化成最简分数。
÷
÷
3
4
15
20
=
15 ( )
20 ( )
=
( )
( )
5
5
÷
÷
4
5
48
60
=
48 ( )
60 ( )
=
( )
( )
12
12
7.下面哪些分数没有化成最简分数?请把它们化成最简分数?
2.约分时,可以一步一步进行约分,每一步都是分子和分母同时除以它们的公因数。也可以用分子和分母同时除以它们的最大公因数,一次约分成最简分数。
约 分
1.把分数化成和它相等,但是分子和分母较小的分数就叫做约分。约分时一般要约成最简分数。
3.逐次除以大于1的公因数,最后得到最简分数的方法叫做“逐次约分法”。 一次除以最大公因数直接得到最简分数的方法叫做“一次约分法”。
1.在线完成4.4约分课后作业。
2.同学说说约分的方法。
再见
约 分
进一步理解分数的基本性质。
能应用分数的基本性质把一个分数化成最简分数。
1.填一填。
3
1
=
6
( )
4
1
=
( )
5
20
4
=
=
20÷ ( )
4÷ ( )
( )
1
20
4
4
5
2
10
3
=
=
10×( )
3 × ( )
( )
30
3
3
9
2.判断每组的两个分数是否相等,并说明理由。
观察这三个分数你有什么发现?
=
﹦
两张大小相同的正方形纸片,请你用其中一张纸片表示出它的 ,
用另外一个正方形表示出和 相等,但是分子、分母比较小的分数。
16
4
16
4
﹦
﹦
﹦
﹦
﹦
﹦
在这三组相等的分数中你喜欢哪几个分数?
请你仔细观察这些最简分数看看它们有什么共同的特点?
﹦
﹦
这三个分数大小一样,看上去你更喜欢哪个分数,说说理由。
用你自己的话说说什么是最简分数。
把分数化成和它相等,但是分子和分母较小的分数就叫做 约分。约分时一般要约成最简分数。
﹦
﹦
如果没有纸片帮忙,你能把这个分数约分吗?
可以用分子和分母的公因数(1除外)去除。
﹦
16
4
16÷2
4÷2
﹦
﹦
8
2
8÷2
2÷2
﹦
4
1
自己独立想一想,把 约分成一个最简分数。
分步约分:
﹦
30
24
30÷6
24÷6
﹦
5
4
﹦
30
24
30÷2
24÷2
﹦
﹦
15
12
15÷3
12÷3
﹦
5
4
用24和30的最大公因数是6约分。
两种约分的方法都对吗?它们有什么相同的地方呢?
方法一是:一步一步进行约分,每一步都是分子和分母同时除以它们的公因数。
逐次除以大于1的公因数,最后得到最简分数的方法叫做“逐次约分法”。
一次除以最大公因数直接得到最简分数的方法叫做“一次约分法”。
方法二是:一次约分成最简分数,是分子和分母同时除以它们的最大公因数。
这两种约分方法都应用了分数的基本性质,它们有什么不同之处吗?
或者
30
24
12
15
4
5
=
5
4
30
24
5
4
5
4
=
约分过程还可以这样写,在约分的过程中划右斜线,所 得的商分别写在分母的正下方和分子的正上方。
1.请你用喜欢的方式约分 和 。
60
15
75
25
60
15
5
20
1
4
=
4
1
75
25
5
15
1
3
=
3
1
9
2. 下列分数中哪些是最简分数,把不是最简分数的化成最简分数。
5
4
4
3
1
4
5
3. 把上下两行相等的两个分数用线连起来。
4.红色部分和黄色部分哪个多些?为什么?
一样大,因为两个部分都占整个圆的 。
5.观察下面的每个分数的分子和分母,哪些有公因数2?哪些有公因数5?哪些有公因数3?
2
3、5
3
3、5
2、5
2、3
6.把下面分数化成最简分数。
÷
÷
3
4
15
20
=
15 ( )
20 ( )
=
( )
( )
5
5
÷
÷
4
5
48
60
=
48 ( )
60 ( )
=
( )
( )
12
12
7.下面哪些分数没有化成最简分数?请把它们化成最简分数?
2.约分时,可以一步一步进行约分,每一步都是分子和分母同时除以它们的公因数。也可以用分子和分母同时除以它们的最大公因数,一次约分成最简分数。
约 分
1.把分数化成和它相等,但是分子和分母较小的分数就叫做约分。约分时一般要约成最简分数。
3.逐次除以大于1的公因数,最后得到最简分数的方法叫做“逐次约分法”。 一次除以最大公因数直接得到最简分数的方法叫做“一次约分法”。
1.在线完成4.4约分课后作业。
2.同学说说约分的方法。
再见
