人教版数学五年级下册 8.2运用优化策略解决问题 课件(22张PPT)
文档属性
| 名称 | 人教版数学五年级下册 8.2运用优化策略解决问题 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 19:40:14 | ||
图片预览







文档简介
(共22张PPT)
运用优化策略解决问题
能够借助纸笔对“找次品”问题进行分析,归纳出解决这类问题的最优策略。
体会解决问题策略的多样性及运用优化的方法解决问题的有效性。
01
02
本节目标
1、有6颗外观一样的保龄球,其中5颗一样重,另外一颗轻一些,如果用天平称几次才能保证称出来。
答:最少需要称2次就能保证可以找出来。
复习旧知
2、有7颗外观一样的巧克力,其中6颗一样重,另外一颗轻一些,如果用天平称几次才能保证称出来。
答:最少需要称2次就能保证可以找出来。
复习旧知
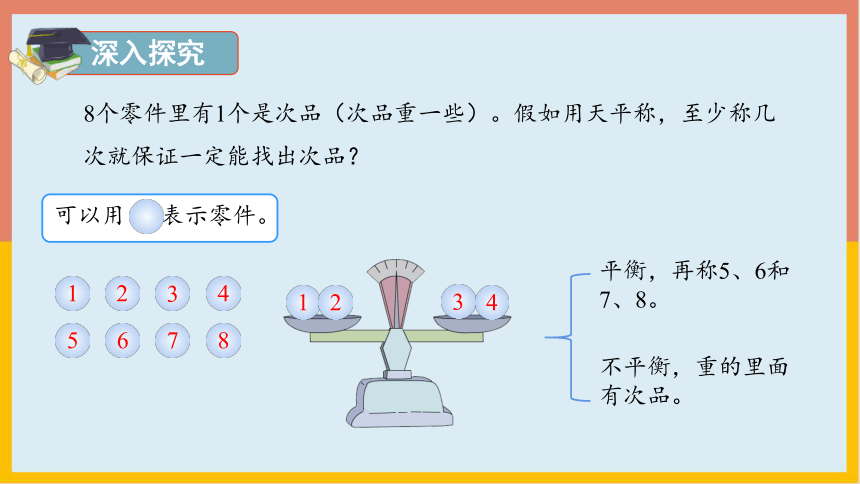
8个零件里有1个是次品(次品重一些)。假如用天平称,
至少称几次就保证一定能找出次品?
是什么意思?
是指肯定能找出次品的最少次数。
深入探究
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次就保证一定能找出次品?
平衡,再称5、6和7、8。
不平衡,重的里面有次品。
可以用 表示零件。
1
2
3
4
5
6
7
8
1
2
3
4
深入探究
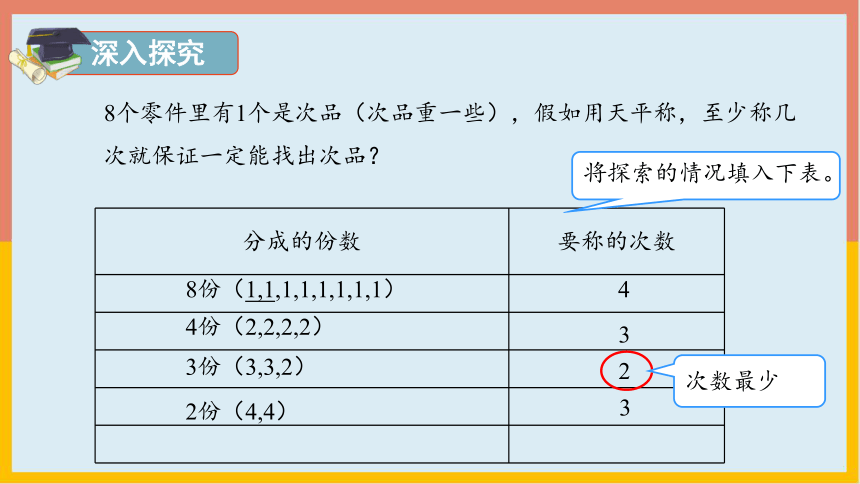
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品?
分成的份数 要称的次数
将探索的情况填入下表。
4份(2,2,2,2)
3
8份(1,1,1,1,1,1,1,1)
4
3份(3,3,2)
2
2份(4,4)
3
次数最少
深入探究
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品?
分成的份数、分的方法与找出次品所要称的次数有什么关系?怎样分找出次品需要称的次数最少呢?
利用天平找次品的时候,把待分的物品分成3份,能够平均分的平均分成3份。不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
深入探究
有9个乒乓球,其中有一个次品(比较轻一些),几次可以保证找出来?
第一次 第二次 第三次 第四次
9(4,4,1)
4(1,1,2)
2(1,1)
9(3,3,3)
3(1,1,1)
9(2,2,5)
5(2,2,1)
2(1,1)
9(1,1,7)
7(1,1,5)
5(1,1,3)
3(1,1,1)
将探索的情况填入下表。比一比那种方法好。
深入探究
如果是12个、22个、27个,几次可以保证找出来?画一画,填一填。
第一次 第二次 第三次 第四次
深入探究
个数 分成的份数 保证能找出的最少次数
3
3(1,1,1)
1
9
2
9(3,3,3)
27
27(9,9,9)
3
通过前面的探究,你发现了什么?
8
2
8(3,3,2)
深入探究
1、1箱饼干有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋饼干来?
接着把找的过程表示出来。
12袋饼干
12袋
巩固练习
12袋饼干
平衡
不平衡
次品在较轻的4袋中,把它分成3份,天平两边各放1袋。
次品在剩下的4袋中,把它分成3份,天平两边各放1袋。
再需要一次保证找出这袋饼干来。
巩固练习
1、1箱饼干有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋饼干来?
2
2
2
2
5
5
平衡,次品在6箱中
不平衡,次品在轻的一侧5箱中
平衡,次品在没称的2箱中
不平衡,次品在轻的一侧2箱中
平衡,剩下1箱是次品
不平衡,次品在轻的一侧2箱中
把有次品的2箱分别放在天平两侧,轻的一侧为次品。
答:最少需要称3次就能保证可以找出这一箱。
6
把16箱饼干分成3份(5 ,5, 6)
2
1
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
巩固练习
也可以这样表示:16
5 5 6
2 2 1
2 2 2
1 1 1 1
答:最少需要称3次就能保证可以找出这一箱。
巩固练习
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
答:最少需要称3次就能保证可以找出这一箱。
还可以这样表示:
16(5,5,6)
5(2,2,1)
6(2,2,2)
2(1,1)
2(1,1)
1
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
巩固练习
3、有24个玻璃球,其中有1个球是次品,比其他球稍轻点,如果只能利用没有砝码的天平来判定哪一个球是次品,请问你最少要称几次才能保证找到这个玻璃球?
至少称3次能保证找到这个玻璃球。
巩固练习
4、在外观相同的20个保龄球中,有一只次品质量略轻,用没有砝码的天平至少称几次,一定可以找出这个次品。
至少称3次能保证找到这个保龄球。
巩固练习
5、有28瓶水,其中27瓶质量相同,另有1瓶是碱水,比其他的水略重一些。至少称几次能保证找出这瓶碱水?
至少称4次能保证找到这瓶碱水。
把28瓶水分成3份(9,9,10)
巩固练习
01
02
能够平均分的平均分成3份。不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
运用优化策略解决问题
利用天平找次品的时候,把待分的物品分成3份。
03
解决问题时可能有很多方法,我们通常是运用最优化策略来解决问题。
本节总结
1、在线完成8.2运用优化策略解决问题课后作业。
2、和你的同学说说解决找次品问题中运用优化策略解决问题的策略。
布置作业
再 见
运用优化策略解决问题
能够借助纸笔对“找次品”问题进行分析,归纳出解决这类问题的最优策略。
体会解决问题策略的多样性及运用优化的方法解决问题的有效性。
01
02
本节目标
1、有6颗外观一样的保龄球,其中5颗一样重,另外一颗轻一些,如果用天平称几次才能保证称出来。
答:最少需要称2次就能保证可以找出来。
复习旧知
2、有7颗外观一样的巧克力,其中6颗一样重,另外一颗轻一些,如果用天平称几次才能保证称出来。
答:最少需要称2次就能保证可以找出来。
复习旧知
8个零件里有1个是次品(次品重一些)。假如用天平称,
至少称几次就保证一定能找出次品?
是什么意思?
是指肯定能找出次品的最少次数。
深入探究
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次就保证一定能找出次品?
平衡,再称5、6和7、8。
不平衡,重的里面有次品。
可以用 表示零件。
1
2
3
4
5
6
7
8
1
2
3
4
深入探究
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品?
分成的份数 要称的次数
将探索的情况填入下表。
4份(2,2,2,2)
3
8份(1,1,1,1,1,1,1,1)
4
3份(3,3,2)
2
2份(4,4)
3
次数最少
深入探究
8个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品?
分成的份数、分的方法与找出次品所要称的次数有什么关系?怎样分找出次品需要称的次数最少呢?
利用天平找次品的时候,把待分的物品分成3份,能够平均分的平均分成3份。不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
深入探究
有9个乒乓球,其中有一个次品(比较轻一些),几次可以保证找出来?
第一次 第二次 第三次 第四次
9(4,4,1)
4(1,1,2)
2(1,1)
9(3,3,3)
3(1,1,1)
9(2,2,5)
5(2,2,1)
2(1,1)
9(1,1,7)
7(1,1,5)
5(1,1,3)
3(1,1,1)
将探索的情况填入下表。比一比那种方法好。
深入探究
如果是12个、22个、27个,几次可以保证找出来?画一画,填一填。
第一次 第二次 第三次 第四次
深入探究
个数 分成的份数 保证能找出的最少次数
3
3(1,1,1)
1
9
2
9(3,3,3)
27
27(9,9,9)
3
通过前面的探究,你发现了什么?
8
2
8(3,3,2)
深入探究
1、1箱饼干有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋饼干来?
接着把找的过程表示出来。
12袋饼干
12袋
巩固练习
12袋饼干
平衡
不平衡
次品在较轻的4袋中,把它分成3份,天平两边各放1袋。
次品在剩下的4袋中,把它分成3份,天平两边各放1袋。
再需要一次保证找出这袋饼干来。
巩固练习
1、1箱饼干有12袋,其中有11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋饼干来?
2
2
2
2
5
5
平衡,次品在6箱中
不平衡,次品在轻的一侧5箱中
平衡,次品在没称的2箱中
不平衡,次品在轻的一侧2箱中
平衡,剩下1箱是次品
不平衡,次品在轻的一侧2箱中
把有次品的2箱分别放在天平两侧,轻的一侧为次品。
答:最少需要称3次就能保证可以找出这一箱。
6
把16箱饼干分成3份(5 ,5, 6)
2
1
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
巩固练习
也可以这样表示:16
5 5 6
2 2 1
2 2 2
1 1 1 1
答:最少需要称3次就能保证可以找出这一箱。
巩固练习
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
答:最少需要称3次就能保证可以找出这一箱。
还可以这样表示:
16(5,5,6)
5(2,2,1)
6(2,2,2)
2(1,1)
2(1,1)
1
2、仓库里有16箱同一规格的可可豆。其中有一箱可可豆质量不够(轻)最少需要称几次就能保证可以找出这一箱?
巩固练习
3、有24个玻璃球,其中有1个球是次品,比其他球稍轻点,如果只能利用没有砝码的天平来判定哪一个球是次品,请问你最少要称几次才能保证找到这个玻璃球?
至少称3次能保证找到这个玻璃球。
巩固练习
4、在外观相同的20个保龄球中,有一只次品质量略轻,用没有砝码的天平至少称几次,一定可以找出这个次品。
至少称3次能保证找到这个保龄球。
巩固练习
5、有28瓶水,其中27瓶质量相同,另有1瓶是碱水,比其他的水略重一些。至少称几次能保证找出这瓶碱水?
至少称4次能保证找到这瓶碱水。
把28瓶水分成3份(9,9,10)
巩固练习
01
02
能够平均分的平均分成3份。不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
运用优化策略解决问题
利用天平找次品的时候,把待分的物品分成3份。
03
解决问题时可能有很多方法,我们通常是运用最优化策略来解决问题。
本节总结
1、在线完成8.2运用优化策略解决问题课后作业。
2、和你的同学说说解决找次品问题中运用优化策略解决问题的策略。
布置作业
再 见
