安徽省安庆市怀宁县第二中学2022届高三上学期12月第四次月考数学(理)试题(Word版含答案解析)
文档属性
| 名称 | 安徽省安庆市怀宁县第二中学2022届高三上学期12月第四次月考数学(理)试题(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 554.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 22:33:57 | ||
图片预览




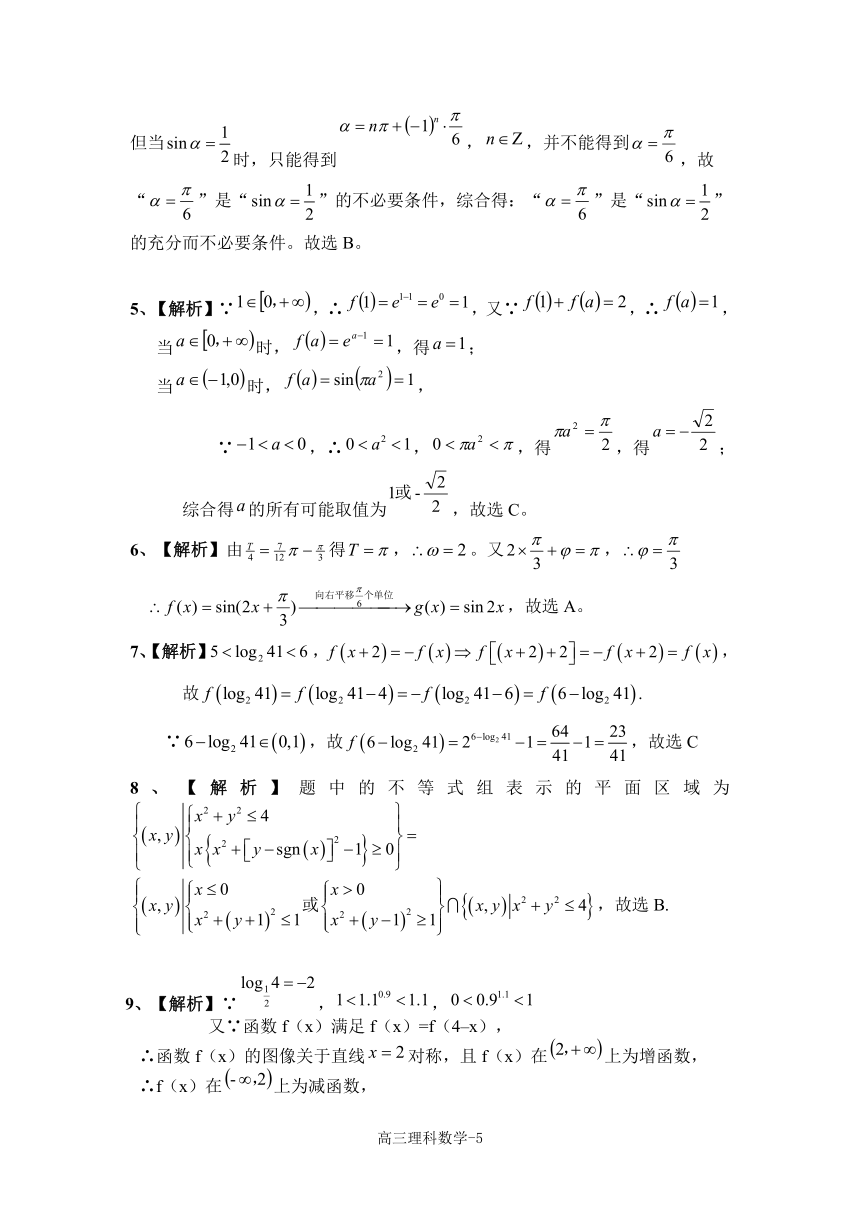
文档简介
怀宁县第二中学2022届高三上学期第四次月考
数学试题(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合,,则为()
A、 B、 C、 D、
2、若,则下列不等式成立的是 ()
A、 B、 C、 D、
3、列函数既有零点,又是单调函数的是 ()
A、 B、 C、 D、
4、“”是“”的
A、既不充分也不必要条件 B、充分而不必要条件
C、必要而不充分条件 D、充分必要条件
5、满足,则的所有可能取值为
A、 B、 C、 D、
6、函数(其中,)的图象如图所示,为了得到的图象,则只需将的图象
A、向右平移个长度单位 B、向右平移个长度单位
C、向左平移个长度单位 D、向左平移个长度单位
7、已知是R上的奇函数,且对,有,当时,,则
A、40 B、 C、 D、
8、太极图被称为“中华第一图”.从孔庙大成殿梁柱,到老子楼观台、三茅宫、白云观的标记物;到中医、气功、武术及中国传统文化的书刊封面、会徽、会标这种广为人知的太极图,其形状如阴阳两鱼互纠在一起,因而被习称为“阴阳鱼太极图”。已知函数,则以下图形中,阴影部分可以用不等式组表示的是
A、B、C、 D、
9、设函数f(x)满足f(x)=f(4–x),当x>2时,f(x)为增函数,则a =f(1.10.9),b =f(0.91.1),c =f(log)的大小关系是
A、a>b>c B、b>a>c C、a>c>b D、c>b>a
10、已知在上为减函数,则的取值范围为
A、 B、 C、 D、
11、已知函数,若等比数列满足,则
A、2021 B、 C、2 D、
12、设函数是定义在上的奇函数,函数是函数的导函数,当时,,则不等式的解集为
A、 B、
C、 D、
二、填空题:本大题共4小题,每小题5分,共20分.
13、设向量,满足,,且,则__________。
14、已知角的终边与单位圆交于点,则的值为_________。
15、若函数在其定义域内的一个子区间内不是单调函数,则实数k 的取值范围是 。
16、若直角坐标平面内M、N两点满足:
①点M、N都在函数f(x)的图像上;
②点M、N关于原点对称,则称这两点M、N是函数f(x)的一对“靓点”。
已知函数则函数f(x)有 对“靓点”。
三、解答题:本大题共6小题,共70分
17、(本小题满分10分)
命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
q:函数f(x)=(3-2a)x是增函数,若p或q为真,p且q为假,
求实数a的取值范围.
18、(本小题满分12分)
已知向量,,
(Ⅰ)求并求的单调递增区间;
(Ⅱ)若,且与共线,为第二象限角,求的值。
19、(本小题满分12分)
在中,角的对边分别为,且.
(Ⅰ)求角的大小;
(Ⅱ)若边上的中线的长为,求面积的最大值.
20、(本小题满分12分)
已知f(x)=sin2x-2sin·sin.
(Ⅰ)若tan α=2,求f(α)的值;
(Ⅱ)若x∈,求f(x)的取值范围.
21、(本小题满分12分)
(12分)已知函数,.
(1)讨论函数f(x)的单调区间;
(2)若对恒成立,求a的取值范围.
22、(本小题满分12分)
已知函数
(Ⅰ)若曲线在点处的切线与直线垂直,求函数的单调区间;
(Ⅱ)若对都有成立,试求实数a的取值范围;
(Ⅲ)记,当a=1时,函数在区间上有两个零点,求实数b的取值范围.
怀宁县第二中学2022届高三上学期第四次月考
数学试题(理科)参考答案
一、选择题:本大题共12小题,每小题5分,共60分
1、【解析】,,故选A。
2、【解析】,,故选C。
3、【解析】∵对于A,函数在R上单调递增且没有零点;对于B,函数在 单调递减,在单调递增,它有两个零点和;对于C,函数在单调递减,在单调递减,它有一个零点;对于D,函数在上单调递增,且有一个零点;故选D。
4、【解析】由,可以得到,故“”是“”的充分条件,
但当时,只能得到,,并不能得到,故“”是“”的不必要条件,综合得:“”是“”的充分而不必要条件。故选B。
5、【解析】∵,∴,又∵,∴,
当时,,得;
当时,,
∵,∴,,得,得;
综合得的所有可能取值为,故选C。
6、【解析】由得,。又,
,故选A。
7、【解析】,,
故.
∵,故,故选C
8、【解析】题中的不等式组表示的平面区域为
,故选B.
9、【解析】∵,,
又∵函数f(x)满足f(x)=f(4–x),
∴函数f(x)的图像关于直线对称,且f(x)在上为增函数,
∴f(x)在上为减函数,
又,
∴,∴,故选D。
10、【解析】令,;令,,
则,
∵,∴函数,为减函数
又∵,为减函数
根据复合函数的单调性可知,函数,单调递增,且,
∴,解得,故实数的取值范围为。故选C。
11、【解析】∵,∴
∵为等比数列,∴,
,…,,,
则,故选A。
12、【解析】令,则,
∵,
∴在上单调递减,且,
∴当时,,而,
即时,;
当时,,而,
即时,;
故在和上都有,
又由为奇函数,故在和上都有,
或,可解得或,
故的取值范围为,故选C。
二、填空题:本大题共4小题,每小题5分,共20分
13、【解析】由题意可知,,
又∵,
∴,故填。
14、【解析】由题意,
则,
故填。
15、【解析】令得,∴且得,故填。
16、【解析】
,故填1。
三、解答题:本大题共6小题,共70分,第17题10分,其余每题12分
17、解:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
所以函数g(x)的图象开口向上且与x轴没有交点,
故Δ=4a2-16<0,∴-2<a<2.
又∵函数f(x)=(3-2a)x是增函数,
∴3-2a>1,∴a<1.
又由于p或q为真命题,p且q为假命题,可知命题p和命题q一真一假
(1)若命题p为真命题,命题q为假命题,则,∴
(2)若命题p为假命题,命题q为真命题,则,∴
综上所述,所求实数的取值范围为
18、解:(Ⅰ)的增区间
是
(Ⅰ),
由于为第二象限角所以,
19、解:(Ⅰ)由及正弦定理可得,
又∵,∴,
∴
∴,得,
又∵,∴,
∴,又∵,∴;
(Ⅱ)∵,
∴,
∴,
即,
∴,,
又∵,当且仅当时“=”成立,
∴,∴,
∴,
故的面积的最大值为。
20、解 :(Ⅰ)f(x)=(sin2x+sin xcos x)+2sin·cos
=+sin 2x+sin
=+(sin 2x-cos 2x)+cos 2x
=(sin 2x+cos 2x)+.
由tan α=2,得sin 2α===.
cos 2α===-.
所以f(α)=(sin 2α+cos 2α)+=.
(Ⅱ)由(Ⅰ)得f(x)=(sin 2x+cos 2x)+=sin+.
由x∈,得2x+∈.
∴-≤sin≤1,∴0≤f(x)≤,
所以f(x)的取值范围是.
21、解:(1),
当时,,在R上单调通增,
当时,令,得,
当时,,在上单调递减,
当时,,在上单调递增,
(2)设
,
即对恒成立,
,
令,对恒成立,
,
①当,即时,
,在上单调递增,
,
,
又,,
②当,即时,
则存在唯一的使,,
当时,,
当时,,
即时,单调递减,时,单调递增,
故,
解得,,
又而在上单调递增,
,解得,
综上,实数a的取值范围为.
22、(本小题满分12分)
解:(Ⅰ)直线的斜率为1.
函数的定义域为,,
所以,解得………1分
所以,
,得x>2; 得0所以f(x)的单调递增区间是(2,+),单调递减区间(0,2) ..…3分
(Ⅱ)==,,
得,得
所以f(x)的单调递增区间是(,+),单调递减区间(0, )
当x=时,取极小值,也就是最小值= ……5分
对都有成立,∴>2
>2,………6分
∴, ,.实数a的取值范围(0, ) ……..…7分
(Ⅲ)当=1时,=,(x>0)
=,由>0得x>1, 由<0得0所以的单调递增区间是(1,+),单调递减区间(0, 1)
x=1时取得极小值. ………10分
因为函数在区间上有两个零点,所以 ……11分
解得.
所以的取值范围是. ……………12分
高三理科数学-3
数学试题(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合,,则为()
A、 B、 C、 D、
2、若,则下列不等式成立的是 ()
A、 B、 C、 D、
3、列函数既有零点,又是单调函数的是 ()
A、 B、 C、 D、
4、“”是“”的
A、既不充分也不必要条件 B、充分而不必要条件
C、必要而不充分条件 D、充分必要条件
5、满足,则的所有可能取值为
A、 B、 C、 D、
6、函数(其中,)的图象如图所示,为了得到的图象,则只需将的图象
A、向右平移个长度单位 B、向右平移个长度单位
C、向左平移个长度单位 D、向左平移个长度单位
7、已知是R上的奇函数,且对,有,当时,,则
A、40 B、 C、 D、
8、太极图被称为“中华第一图”.从孔庙大成殿梁柱,到老子楼观台、三茅宫、白云观的标记物;到中医、气功、武术及中国传统文化的书刊封面、会徽、会标这种广为人知的太极图,其形状如阴阳两鱼互纠在一起,因而被习称为“阴阳鱼太极图”。已知函数,则以下图形中,阴影部分可以用不等式组表示的是
A、B、C、 D、
9、设函数f(x)满足f(x)=f(4–x),当x>2时,f(x)为增函数,则a =f(1.10.9),b =f(0.91.1),c =f(log)的大小关系是
A、a>b>c B、b>a>c C、a>c>b D、c>b>a
10、已知在上为减函数,则的取值范围为
A、 B、 C、 D、
11、已知函数,若等比数列满足,则
A、2021 B、 C、2 D、
12、设函数是定义在上的奇函数,函数是函数的导函数,当时,,则不等式的解集为
A、 B、
C、 D、
二、填空题:本大题共4小题,每小题5分,共20分.
13、设向量,满足,,且,则__________。
14、已知角的终边与单位圆交于点,则的值为_________。
15、若函数在其定义域内的一个子区间内不是单调函数,则实数k 的取值范围是 。
16、若直角坐标平面内M、N两点满足:
①点M、N都在函数f(x)的图像上;
②点M、N关于原点对称,则称这两点M、N是函数f(x)的一对“靓点”。
已知函数则函数f(x)有 对“靓点”。
三、解答题:本大题共6小题,共70分
17、(本小题满分10分)
命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
q:函数f(x)=(3-2a)x是增函数,若p或q为真,p且q为假,
求实数a的取值范围.
18、(本小题满分12分)
已知向量,,
(Ⅰ)求并求的单调递增区间;
(Ⅱ)若,且与共线,为第二象限角,求的值。
19、(本小题满分12分)
在中,角的对边分别为,且.
(Ⅰ)求角的大小;
(Ⅱ)若边上的中线的长为,求面积的最大值.
20、(本小题满分12分)
已知f(x)=sin2x-2sin·sin.
(Ⅰ)若tan α=2,求f(α)的值;
(Ⅱ)若x∈,求f(x)的取值范围.
21、(本小题满分12分)
(12分)已知函数,.
(1)讨论函数f(x)的单调区间;
(2)若对恒成立,求a的取值范围.
22、(本小题满分12分)
已知函数
(Ⅰ)若曲线在点处的切线与直线垂直,求函数的单调区间;
(Ⅱ)若对都有成立,试求实数a的取值范围;
(Ⅲ)记,当a=1时,函数在区间上有两个零点,求实数b的取值范围.
怀宁县第二中学2022届高三上学期第四次月考
数学试题(理科)参考答案
一、选择题:本大题共12小题,每小题5分,共60分
1、【解析】,,故选A。
2、【解析】,,故选C。
3、【解析】∵对于A,函数在R上单调递增且没有零点;对于B,函数在 单调递减,在单调递增,它有两个零点和;对于C,函数在单调递减,在单调递减,它有一个零点;对于D,函数在上单调递增,且有一个零点;故选D。
4、【解析】由,可以得到,故“”是“”的充分条件,
但当时,只能得到,,并不能得到,故“”是“”的不必要条件,综合得:“”是“”的充分而不必要条件。故选B。
5、【解析】∵,∴,又∵,∴,
当时,,得;
当时,,
∵,∴,,得,得;
综合得的所有可能取值为,故选C。
6、【解析】由得,。又,
,故选A。
7、【解析】,,
故.
∵,故,故选C
8、【解析】题中的不等式组表示的平面区域为
,故选B.
9、【解析】∵,,
又∵函数f(x)满足f(x)=f(4–x),
∴函数f(x)的图像关于直线对称,且f(x)在上为增函数,
∴f(x)在上为减函数,
又,
∴,∴,故选D。
10、【解析】令,;令,,
则,
∵,∴函数,为减函数
又∵,为减函数
根据复合函数的单调性可知,函数,单调递增,且,
∴,解得,故实数的取值范围为。故选C。
11、【解析】∵,∴
∵为等比数列,∴,
,…,,,
则,故选A。
12、【解析】令,则,
∵,
∴在上单调递减,且,
∴当时,,而,
即时,;
当时,,而,
即时,;
故在和上都有,
又由为奇函数,故在和上都有,
或,可解得或,
故的取值范围为,故选C。
二、填空题:本大题共4小题,每小题5分,共20分
13、【解析】由题意可知,,
又∵,
∴,故填。
14、【解析】由题意,
则,
故填。
15、【解析】令得,∴且得,故填。
16、【解析】
,故填1。
三、解答题:本大题共6小题,共70分,第17题10分,其余每题12分
17、解:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
所以函数g(x)的图象开口向上且与x轴没有交点,
故Δ=4a2-16<0,∴-2<a<2.
又∵函数f(x)=(3-2a)x是增函数,
∴3-2a>1,∴a<1.
又由于p或q为真命题,p且q为假命题,可知命题p和命题q一真一假
(1)若命题p为真命题,命题q为假命题,则,∴
(2)若命题p为假命题,命题q为真命题,则,∴
综上所述,所求实数的取值范围为
18、解:(Ⅰ)的增区间
是
(Ⅰ),
由于为第二象限角所以,
19、解:(Ⅰ)由及正弦定理可得,
又∵,∴,
∴
∴,得,
又∵,∴,
∴,又∵,∴;
(Ⅱ)∵,
∴,
∴,
即,
∴,,
又∵,当且仅当时“=”成立,
∴,∴,
∴,
故的面积的最大值为。
20、解 :(Ⅰ)f(x)=(sin2x+sin xcos x)+2sin·cos
=+sin 2x+sin
=+(sin 2x-cos 2x)+cos 2x
=(sin 2x+cos 2x)+.
由tan α=2,得sin 2α===.
cos 2α===-.
所以f(α)=(sin 2α+cos 2α)+=.
(Ⅱ)由(Ⅰ)得f(x)=(sin 2x+cos 2x)+=sin+.
由x∈,得2x+∈.
∴-≤sin≤1,∴0≤f(x)≤,
所以f(x)的取值范围是.
21、解:(1),
当时,,在R上单调通增,
当时,令,得,
当时,,在上单调递减,
当时,,在上单调递增,
(2)设
,
即对恒成立,
,
令,对恒成立,
,
①当,即时,
,在上单调递增,
,
,
又,,
②当,即时,
则存在唯一的使,,
当时,,
当时,,
即时,单调递减,时,单调递增,
故,
解得,,
又而在上单调递增,
,解得,
综上,实数a的取值范围为.
22、(本小题满分12分)
解:(Ⅰ)直线的斜率为1.
函数的定义域为,,
所以,解得………1分
所以,
,得x>2; 得0
(Ⅱ)==,,
得,得
所以f(x)的单调递增区间是(,+),单调递减区间(0, )
当x=时,取极小值,也就是最小值= ……5分
对都有成立,∴>2
>2,………6分
∴, ,.实数a的取值范围(0, ) ……..…7分
(Ⅲ)当=1时,=,(x>0)
=,由>0得x>1, 由<0得0
x=1时取得极小值. ………10分
因为函数在区间上有两个零点,所以 ……11分
解得.
所以的取值范围是. ……………12分
高三理科数学-3
同课章节目录
