三角形和图形的运动(二)(课件)人教版 数学四年级下册(共23张PPT)
文档属性
| 名称 | 三角形和图形的运动(二)(课件)人教版 数学四年级下册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 837.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 12:13:36 | ||
图片预览






文档简介
(共23张PPT)
观察物体(二)
三角形和图形的运动(二)
对所学的观察物体、三角形和图形的运动知识内容有进一步的理解,巩固所学。
初步学会从知识领域的角度回顾梳理知识,体会知识间的内在联系,并进一步养成回顾与整理知识的良好学习习惯。
01
02
观察物体
三角形
观察物体(二)、三角形和图形的运动(二)
图形的运动
从不同方向观察同一物体,看到的形状可能不相同。从同一位置观察由相同个数的小正方体拼摆的物体,看到的形状有的相同、有的不同。
知识点1:观察物体
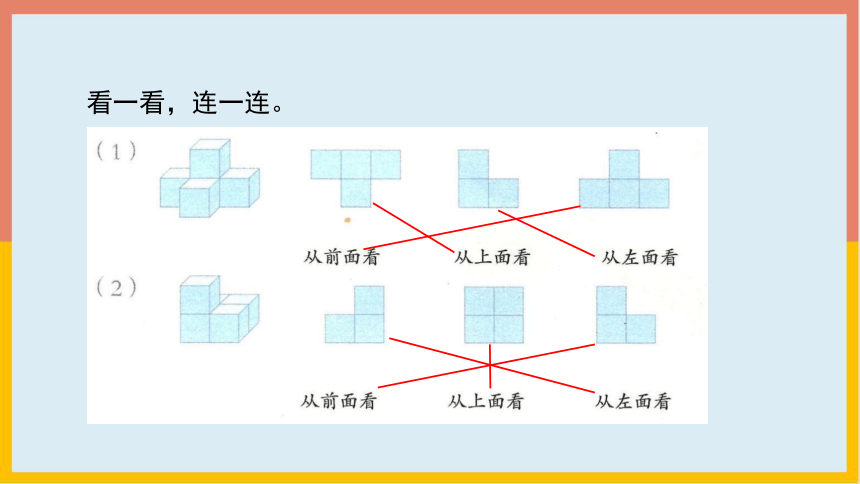
看一看,连一连。
从前面看
从左面看
从上面看
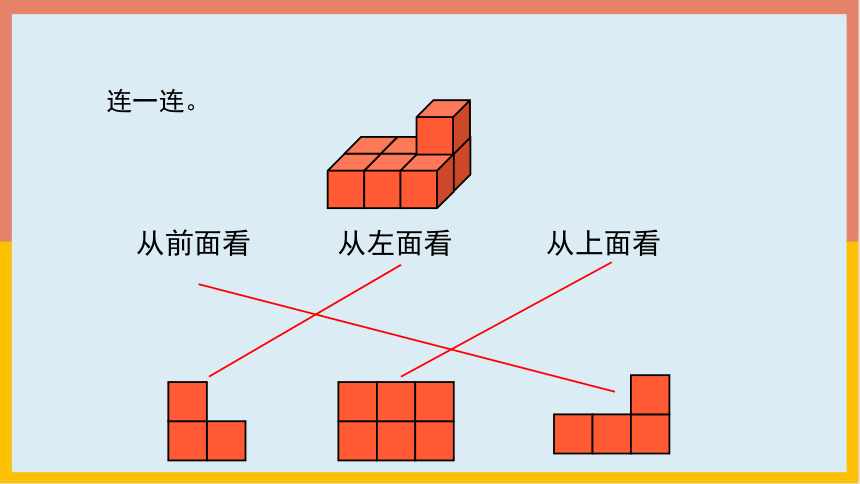
连一连。
知识点2:三角形
三角形具有稳定性。
两点之间,线段最短,这条线段的长度叫做两点间的距离。
三角形的任意两边的和大于第三边。
按角分:锐角三角形、直角三角形、钝角三角形。
按边分:等腰三角形(包括等边三角形)、不等边三角形。
三角形内角和是180°。
任意四边形的内角和是360°。
多边形内角和=180°×(边数-2)
在( )里填上适当的数或文字。
(1)小明准备用图钉固定硬纸条做一个三角形。他应该准备( )根硬纸条,因为三角形有( )条边,他应该准备( )个图 钉,因为三角形有三个( )。
(2)红领巾按角分类属于( )三角形,按边分类属于( )三角形。
(3)等边三角形的每个内角都是( )°,等腰直角三角形的一个底角是( )° 。
3
3
3
顶点
钝角
等腰
60
45
下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)在一个三角形中,如果有两个锐角,那么这个三角形就一定是锐角三角形。 ( )
×
(2)钝角三角形只有一条高。 ( )
×
(3)锐角三角形中任意两个锐角的和一定大于90°。 ( )
√
对称轴两侧的对应点到对称轴的距离相等。
根据对称轴补全轴对称图形的方法:
1.定点 2.画出对称点 3.连点成形。
图形平移的画法:
1.选点 2.移点 3.连点成形。
知识点3:图形的运动
先根据对称轴补全下面这个轴对称图形,再画出向右平移14格后的图形。
先补全下面这个轴对称图形,再画出向右平移4格后的图形。
1、你能算出下面这幅小鱼图形的面积是多少吗?
小鱼图形的面积是6cm2
2、把一个等边三角形分成4个相等的小的等边三角形。在下边的图里画一画。
3、在( )里填上适当的数。
( )个锐角,( )个锐角三角形。
( )个钝角,( )个钝角三角形。
( )个直角,( )个直角三角形。
10
2
2
2
4
4
观察物体(二)、三角形和图形的运动(二)
观察物体
三角形
图形的运动
从前面、上面、左面观察物体
观察由几个正方体摆成的组合体
三角形的特性
三角形的分类
三角形的内角和
轴对称
平移
(1)把一个大三角形剪成两个小三角形,每个小三角形的内角和是90°。 ( )
×
(2)一个等腰三角形的周长是21厘米,底边长是3厘米,则腰长是9厘米。 ( )
√
(3)有一个角是60°的等腰三角形一定是一个等边三角形 。
( )
√
1、下面的说法正确吗?正确的画“√”,错误的画“×”。
2、在下表中适当的空格内画上“√”,再说一说几种三角形之间的联系和区别。
图形名称 三条边都相等 只有两条边相等 有一个角是直角 只有两个锐角 有三个锐角
等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
√
√
√
√
√
√
√
3、在( )里填一填。
从( )面看
从( )面看
从( )面看
上
前
左
4、如果一个三角形的两条边分别是4cm和7cm,另一条边可能是几厘米(取整数值)?
4+7=11(cm)
3+4=7(cm)
3cm<第三条边<11cm
答:另一条边可能是4cm或5cm或6cm
或7cm或8cm或9cm或10cm。
我知道三角形
任意两边的和
大于第三边。
因为3+4=7,所以第三边要比3大,并且还要比11小。
(1)房屋的屋架做成三角形是运用了( )。
(2)下图中,与线段AB对应的高是线段( ),与线段BC对应的高是线段( )。
A
B
C
D
三角形的稳定性
AC
AD
5、在( )里填上适当的数或文字。
在线完成观察物体(二)、三角形和图形的运动(二)期末检测
观察物体(二)
三角形和图形的运动(二)
对所学的观察物体、三角形和图形的运动知识内容有进一步的理解,巩固所学。
初步学会从知识领域的角度回顾梳理知识,体会知识间的内在联系,并进一步养成回顾与整理知识的良好学习习惯。
01
02
观察物体
三角形
观察物体(二)、三角形和图形的运动(二)
图形的运动
从不同方向观察同一物体,看到的形状可能不相同。从同一位置观察由相同个数的小正方体拼摆的物体,看到的形状有的相同、有的不同。
知识点1:观察物体
看一看,连一连。
从前面看
从左面看
从上面看
连一连。
知识点2:三角形
三角形具有稳定性。
两点之间,线段最短,这条线段的长度叫做两点间的距离。
三角形的任意两边的和大于第三边。
按角分:锐角三角形、直角三角形、钝角三角形。
按边分:等腰三角形(包括等边三角形)、不等边三角形。
三角形内角和是180°。
任意四边形的内角和是360°。
多边形内角和=180°×(边数-2)
在( )里填上适当的数或文字。
(1)小明准备用图钉固定硬纸条做一个三角形。他应该准备( )根硬纸条,因为三角形有( )条边,他应该准备( )个图 钉,因为三角形有三个( )。
(2)红领巾按角分类属于( )三角形,按边分类属于( )三角形。
(3)等边三角形的每个内角都是( )°,等腰直角三角形的一个底角是( )° 。
3
3
3
顶点
钝角
等腰
60
45
下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)在一个三角形中,如果有两个锐角,那么这个三角形就一定是锐角三角形。 ( )
×
(2)钝角三角形只有一条高。 ( )
×
(3)锐角三角形中任意两个锐角的和一定大于90°。 ( )
√
对称轴两侧的对应点到对称轴的距离相等。
根据对称轴补全轴对称图形的方法:
1.定点 2.画出对称点 3.连点成形。
图形平移的画法:
1.选点 2.移点 3.连点成形。
知识点3:图形的运动
先根据对称轴补全下面这个轴对称图形,再画出向右平移14格后的图形。
先补全下面这个轴对称图形,再画出向右平移4格后的图形。
1、你能算出下面这幅小鱼图形的面积是多少吗?
小鱼图形的面积是6cm2
2、把一个等边三角形分成4个相等的小的等边三角形。在下边的图里画一画。
3、在( )里填上适当的数。
( )个锐角,( )个锐角三角形。
( )个钝角,( )个钝角三角形。
( )个直角,( )个直角三角形。
10
2
2
2
4
4
观察物体(二)、三角形和图形的运动(二)
观察物体
三角形
图形的运动
从前面、上面、左面观察物体
观察由几个正方体摆成的组合体
三角形的特性
三角形的分类
三角形的内角和
轴对称
平移
(1)把一个大三角形剪成两个小三角形,每个小三角形的内角和是90°。 ( )
×
(2)一个等腰三角形的周长是21厘米,底边长是3厘米,则腰长是9厘米。 ( )
√
(3)有一个角是60°的等腰三角形一定是一个等边三角形 。
( )
√
1、下面的说法正确吗?正确的画“√”,错误的画“×”。
2、在下表中适当的空格内画上“√”,再说一说几种三角形之间的联系和区别。
图形名称 三条边都相等 只有两条边相等 有一个角是直角 只有两个锐角 有三个锐角
等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
√
√
√
√
√
√
√
3、在( )里填一填。
从( )面看
从( )面看
从( )面看
上
前
左
4、如果一个三角形的两条边分别是4cm和7cm,另一条边可能是几厘米(取整数值)?
4+7=11(cm)
3+4=7(cm)
3cm<第三条边<11cm
答:另一条边可能是4cm或5cm或6cm
或7cm或8cm或9cm或10cm。
我知道三角形
任意两边的和
大于第三边。
因为3+4=7,所以第三边要比3大,并且还要比11小。
(1)房屋的屋架做成三角形是运用了( )。
(2)下图中,与线段AB对应的高是线段( ),与线段BC对应的高是线段( )。
A
B
C
D
三角形的稳定性
AC
AD
5、在( )里填上适当的数或文字。
在线完成观察物体(二)、三角形和图形的运动(二)期末检测
