2021-2022学年北师大版九年级数学下册3.6直线和圆的位置关系 同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.6直线和圆的位置关系 同步达标训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 457.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.6直线和圆的位置关系》
同步达标训练(附答案)
1.已知,⊙O的半径是一元二次方程x2﹣5x﹣6=0的一个根,圆心O到直线l的距离d=4,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.平行
2.半径为3的⊙P的圆心坐标为(2,4),则⊙P与x轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
3.如图,AB是圆O的直径,点C在BA的延长线上,直线CD与圆O相切于点D,弦DF⊥AB于点E,连接BD,CD=BD=4,则OE的长度为( )
A. B.2 C.2 D.4
4.如图△MBC中,∠B=90°,∠C=60°,MB=2,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )
A. B. C.2 D.3
5.如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于( )
A.30° B.60° C.90° D.120°
6.如图,点P是⊙O外一点,PAB为⊙O的一条割线,且PA=AB,PO交⊙O于点C,若OC=3,OP=5,则AB长为( )
A. B. C. D.
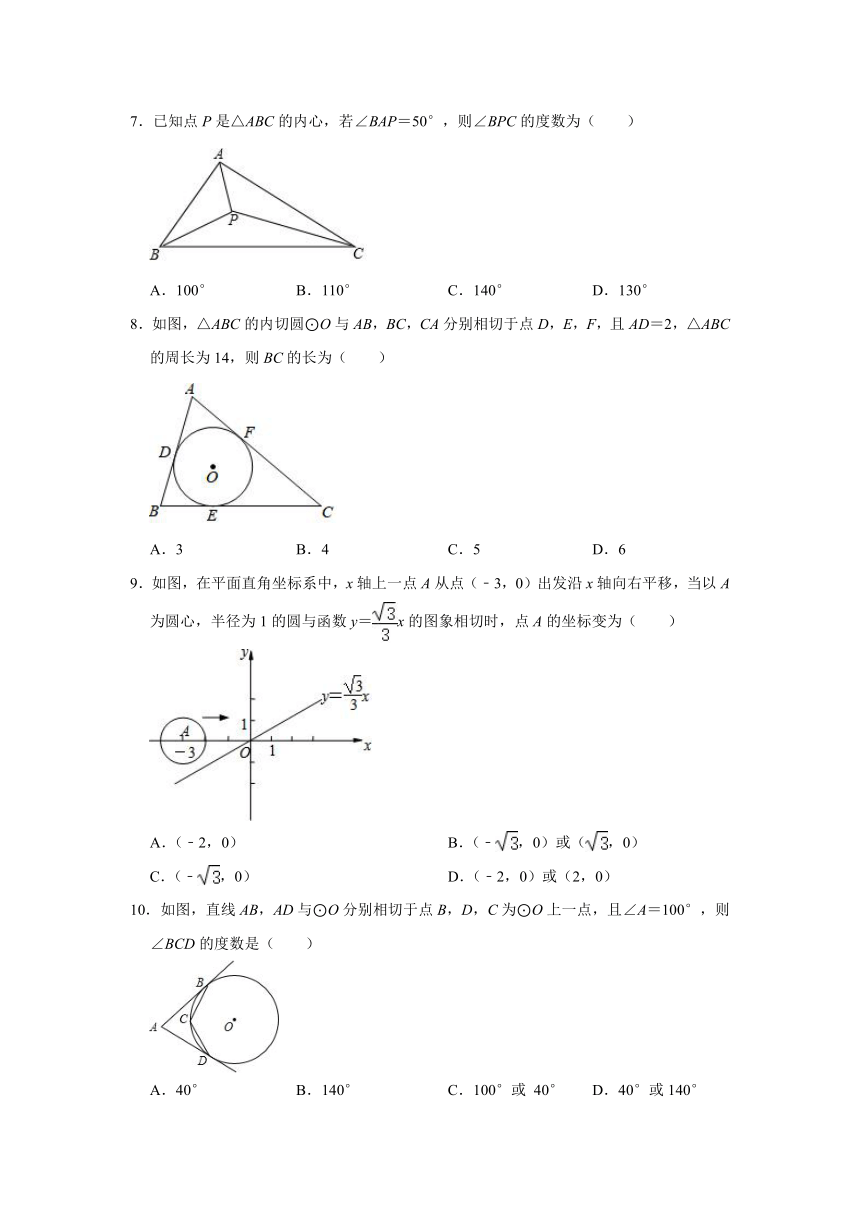
7.已知点P是△ABC的内心,若∠BAP=50°,则∠BPC的度数为( )
A.100° B.110° C.140° D.130°
8.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为( )
A.3 B.4 C.5 D.6
9.如图,在平面直角坐标系中,x轴上一点A从点(﹣3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=x的图象相切时,点A的坐标变为( )
A.(﹣2,0) B.(﹣,0)或(,0)
C.(﹣,0) D.(﹣2,0)或(2,0)
10.如图,直线AB,AD与⊙O分别相切于点B,D,C为⊙O上一点,且∠A=100°,则∠BCD的度数是( )
A.40° B.140° C.100°或 40° D.40°或140°
11.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )
A.l1和l2的距离为2
B.当MN与⊙O相切时,AM=2
C.MN=
D.当∠MON=90°时,MN与⊙O相切
12.如图,点C、O在线段AB上,且AC=CO=OB=5,过点A作以BC为直径的⊙O切线,D为切点,则AD的长为( )
A.5 B.6 C. D.10
13.如图,AB是⊙O的直径,CP切⊙O于点C,交AB的延长线于点P,若∠P=20°,则∠A= .
14.如图,AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切与点D,过点B作PD的垂线,与PD的延长线相交于点C,若⊙O的半径为4,BC=6,则PA的长为 .
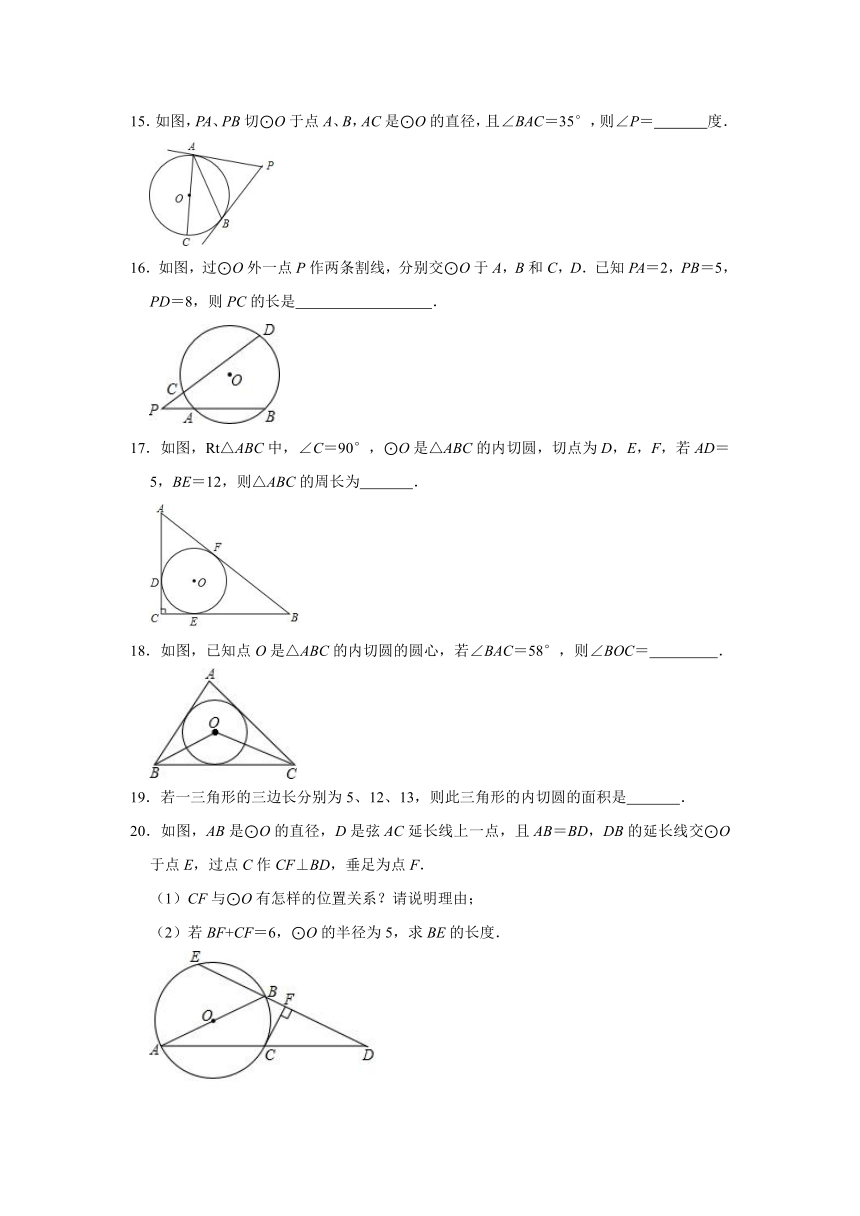
15.如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P= 度.
16.如图,过⊙O外一点P作两条割线,分别交⊙O于A,B和C,D.已知PA=2,PB=5,PD=8,则PC的长是 .
17.如图,Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点为D,E,F,若AD=5,BE=12,则△ABC的周长为 .
18.如图,已知点O是△ABC的内切圆的圆心,若∠BAC=58°,则∠BOC= .
19.若一三角形的三边长分别为5、12、13,则此三角形的内切圆的面积是 .
20.如图,AB是⊙O的直径,D是弦AC延长线上一点,且AB=BD,DB的延长线交⊙O于点E,过点C作CF⊥BD,垂足为点F.
(1)CF与⊙O有怎样的位置关系?请说明理由;
(2)若BF+CF=6,⊙O的半径为5,求BE的长度.
21.如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
22.如图,AB为⊙O直径,C、D为⊙O上的点,CE⊥DB交DB的延长线于点E,且∠CBE=∠ABC.
(1)判断直线CE与⊙O的位置关系,并说明理由;
(2)求证:CD=CA;
(3)若AC=4,AB=5,求CE的长.
23.如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(1)DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
(2)若AD=4、AB=6,求直角边BC的长.
24.如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
25.如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
26.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E.过点D作⊙O的切线,交AC于点F,交AB的延长线于点G,连接DE.
(1)求证:BD=CD;
(2)若∠G=40°,求∠AED的度数.
(3)若BG=6,CF=2,求⊙O的半径.
参考答案
1.解:∵x2﹣5x﹣6=0
∴x1=﹣1,x2=6
∵⊙O的半径为一元二次方程x2﹣5x﹣6=0的根,
∴r=6
∵d<r
∴直线l与⊙O的位置关系是相交
故选:A.
2.解:在直角坐标系内,以P(2,4)为圆心,3为半径画圆,则点P到x轴的距离为d=4,
∵r=3,
∴d>r,
∴⊙P与x轴的相离.
故选:B.
3.解:连接OD,如图,
∵直线CD与⊙O相切于点D,
∴OD⊥CD,
∴∠ODC=90°,
∵CD=BD=4,
∴∠C=∠B,
∵OD=OB,
∴∠B=∠ODB,
∴∠DOE=∠B+∠ODB=2∠B,
∴∠DOE=2∠C,
在Rt△OCD中,∠DOE=2∠C,则∠DOE=60°,∠C=30°,
∴OD=cot∠EOD CD=×4=4,
∵DF⊥AB,
∴∠DEO=90°,
在Rt△ODE中,OE=cos∠EOD OD=×4=2,
故选:B.
4.解:在直角△BCM中,
tan60°==,
得到BC==2,
∵AB为圆O的直径,且AB⊥BC,
∴BC为圆O的切线,又CD也为圆O的切线,
∴CD=BC=2.
故选:C.
5.解:∵DA与△ABC的外接圆相切于点A,
∴∠CAD=∠B=60°.(弦切角定理)
故选:B.
6.解:设PA=AB=x,延长PO交圆于点D.
∵PA PB=PC PD,OC=3,OP=5,
∴x 2x=16,
∴x=2.
故选:B.
7.解:∵点P是△ABC的内心,∠BAP=50°,
∴∠BAC=2∠BAP=100°,
∴∠ABC+∠ACB=80°,
∴∠PBC+∠PCB=80°=40°,
∴∠BPC=180°﹣40°=140°,
故选:C.
8.解:∵⊙O与AB,BC,CA分别相切于点D,E,F
∴AF=AD=2,BD=BE,CE=CF,
∵△ABC的周长为14,
∴AD+AF+BE+BD+CE+CF=14
∴2(BE+CE)=10
∴BC=5
故选:C.
9.解:①当圆A在x轴的负半轴和直线y=x相切时,
由题意得,直线与x轴的交点为30°,
点A到直线的距离为1,则OA=2,
点A的坐标为(﹣2,0);
②当圆A在x轴的正半轴和直线y=x相切时,
由①得,点A的坐标为(2,0);
故选:D.
10.解:当点C在劣弧BC上时,如图1
过点B作直径BE,连接OD、DE.
∵直线AB,AD与⊙O分别相切于点B,D,
∴∠OBA=∠ODA=90°,
∵∠A=100°,
∴∠BOD=80°,
∴∠DOE=100°,
∵OD=OE,
∴∠E=50°,
∵B、C、D、E共圆,
∴∠BCD=180°﹣40°=140°,
当点C在优弧BC′D上时,如图2,∠C′=40°
故选:D.
11.解:连接OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;
作NH⊥AM于H,如图1,
则MN=AB=2,
∵∠AMN=60°,
∴sin60°=,
∴MN==;
当MN与⊙O相切,如图2,连接OM,ON,
当MN在AB左侧时,∠AMO=∠AMN=×60°=30°,
在Rt△AMO中,tan∠AMO=,即AM==,
在Rt△OBN中,∠ONB=∠BNM=60°,tan∠ONB=,即BN==,
当MN在AB右侧时,AM=,
∴AM的长为;
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.
故选:B.
12.解:∵AD是⊙O的切线,ACB是⊙O的割线,
∴AD2=AC AB,
又AC=5,AB=AC+CO+OB=15,
∴AD2=5×15=75,
∴AD=5.(AD=﹣5不合题意舍去).
故选:C.
13.解:连接OC,
∵CP切⊙O于点C,∠P=20°,
∴∠OCP=90°,
∴∠COP=70°,
∵OA=OC,
∴∠OCA=∠A=,
故答案为:35°
14.解:连接DO
解:连接DO,
∵PD与⊙O相切于点D,
∴∠PDO=90°,
∵∠C=90°,
∴DO∥BC,
∴△PDO∽△PCB,
∴
∴
∴PA=4
故答案为4
15.解:连接OB;
∵PA、PB都是⊙O的切线,且切点为A、B,
∴∠OAP=∠OBP=90°,
∴∠AOB+∠P=180°;
在△AOB中,OA=OB,∠AOB=180°﹣2∠BAC;
∴∠P=2∠BAC=70°.
16.解:∵PA PB=PC PD,PA=2,PB=5,PD=8
∴PC==.
17.解:连接EO,DO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥BC,OD⊥AC,BF=BE=12,AD=AF=5,EC=CD,
又∵∠C=90°,
∴四边形ECDO是矩形,
又∵EO=DO,
∴矩形OECD是正方形,
设EO=x,
则EC=CD=x,
在Rt△ABC中
BC2+AC2=AB2
故(x+12)2+(x+5)2=172,
解得:x=3,
∴△ABC的周长=8+15+17=40.
故答案为40.
18.解:∵点O是△ABC的内切圆的圆心,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠BAC=58°,
∴∠ABC+∠ACB=180°﹣∠BAC=122°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣×122°=119°.
故答案为:119°
19.解:∵AC2+BC2=25+144=169,AB2=169,
∴AC2+BC2=AB2,
∴∠C=90°,
连接OE、OQ,
∵圆O是三角形ABC的内切圆,
∴AE=AF,BQ=BF,∠OEC=∠OQC=∠C=90°,OE=OQ,
∴四边形OECQ是正方形,
∴设OE=CE=CQ=OQ=a,
∵AF+BF=13,
∴12﹣a+5﹣a=13,
∴a=2,
∴它的内切圆半径,
∴内切圆面积S=π r2=π×22=4π.
故答案为:4π
20.解:(1)CF与⊙O相切.连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=BD,
∴∠A=∠D,
又∵OA=OB,
∴OC是△ABD的中位线.
∴OC∥BD,
∴∠OCF=∠CFD=90°,
即CF⊥OC.
∴CF与⊙O相切;
(2)过点O作OH⊥BE于点H,则∠OCF=∠CFH=∠OHB=90°,
∴四边形OCFH是矩形,
∴OC=FH,OH=CF,
设BH=x,
∵OC=5,BF+CF=6,
∴BF=5﹣x,OH=CF=6﹣(5﹣x)=x+1,
在Rt△BOH中,由勾股定理知:
BH2+OH2=OB2,即x2+(x+1)2=52,
解得x1=3,x2=﹣4(不合题意,舍去).
∴BH=3,
∵OH⊥BE,
∴BH=EH=BE,
∴BE=2BH=2×3=6.
21.解:(1)连接BD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD==5,
在Rt△ACB中,AB=10,BC=5,
∴AC==5,
答:AC=5,AD=5;
(2)直线PC与⊙O相切,理由是:
连接OC,
在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠COB=60°,
∵∠ACD=45°,
∴∠OCD=45°﹣30°=15°,
∴∠CEP=∠COB+∠OCD=15°+60°=75°,
∵PC=PE,
∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与⊙O相切.
22.解:(1)直线CE与⊙O相切,
理由:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥DB,
∴∠E=90°,
∵∠CBE=∠ABC,
∴∠ECB=∠A,
∵OC=OA,
∴∠A=∠ACO,
∵∠ACO+∠OCB=90°,
∴∠ECB+∠OCB=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)连接AD,
∵AB为⊙O直径,
∴AD⊥DE,
∵CE⊥DE,
∴CE∥AD,
∴∠ECD=∠ADC,
∵CE是⊙O的切线,
∴∠CAD=∠ECD,
∴∠CAD=∠ADC,
∴AC=CD;
(3)∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ACB中,AC=4,AB=5,
∴BC==3,
∵∠CAB=∠∠CDB,
∴Rt△ACB∽Rt△DEC,
∴=,即=,
∴EC=.
23.解:(1)连OD,OE,如图,
∵E是BC边上的中点,AB是半圆O的直径,
∴OE是△ABC的中位线,
∴OE∥AC,
∴∠1=∠3,∠2=∠A,而OD=OA,∠A=∠3,
∴∠1=∠2,
又∵OD=OB,OE为公共边,
∴△OED≌△OEB,
∴∠ODE=∠OBE=90°.
∴DE与半圆O相切.
(2)∵AB为直径
∴∠ADB=∠ABC=90°,
∴∠CAB=∠CAB,
∴△ABC∽△ADB.
∴,
∵AD=4、AB=6,
∴AC=9,
∴在Rt△ABC中:BC===3.
24.(1)证明:连接OD,如图所示:
∵OD=OB,
∴∠1=∠2,
又∵BD平分∠ABC,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥BC,
而∠C=90°,
∴OD⊥AD,
∴AC与⊙O相切于D点;
(2)解:∵OD⊥AD,
∴在RT△OAD中,OA2=OD2+AD2,
又∵AD=15,AE=9,设半径为r,
∴(r+9)2=152+r2,
解方程得,r=8,
即⊙O的半径为8.
25.解:(1)如图连接OD.
∵BD是⊙O的切线,
∴OD⊥BD.
∵AC⊥BD,
∴OD∥AC.
∴∠ODA=∠DAC.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD,即AD平分∠BAC.
(2)OD∥AC,
∴△BOD∽△BAC,
∴=,即=,解得:AC=.
26.(1)证明:连接AD,
∵AB为直径,
∴∠ACB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)解:连接OD,
∵GF是切线,OD是半径,
∴OD⊥GF,
∴∠ODG=90°,
∵∠G=40°,
∴∠GOD=50°,
∵OB=OD,
∴∠OBD=65°,
∵点A、B、D、E都在⊙O上,
∴∠ABD+∠AED=180°,
∴∠AED=115°;
(3)解:∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△GOD∽△GAF,
∴=,
∴设⊙O的半径是r,则AB=AC=2r,
∴AF=2r﹣2,
∴=,
∴r=3,
即⊙O的半径是3.
同步达标训练(附答案)
1.已知,⊙O的半径是一元二次方程x2﹣5x﹣6=0的一个根,圆心O到直线l的距离d=4,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.平行
2.半径为3的⊙P的圆心坐标为(2,4),则⊙P与x轴的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
3.如图,AB是圆O的直径,点C在BA的延长线上,直线CD与圆O相切于点D,弦DF⊥AB于点E,连接BD,CD=BD=4,则OE的长度为( )
A. B.2 C.2 D.4
4.如图△MBC中,∠B=90°,∠C=60°,MB=2,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )
A. B. C.2 D.3
5.如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于( )
A.30° B.60° C.90° D.120°
6.如图,点P是⊙O外一点,PAB为⊙O的一条割线,且PA=AB,PO交⊙O于点C,若OC=3,OP=5,则AB长为( )
A. B. C. D.
7.已知点P是△ABC的内心,若∠BAP=50°,则∠BPC的度数为( )
A.100° B.110° C.140° D.130°
8.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,△ABC的周长为14,则BC的长为( )
A.3 B.4 C.5 D.6
9.如图,在平面直角坐标系中,x轴上一点A从点(﹣3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=x的图象相切时,点A的坐标变为( )
A.(﹣2,0) B.(﹣,0)或(,0)
C.(﹣,0) D.(﹣2,0)或(2,0)
10.如图,直线AB,AD与⊙O分别相切于点B,D,C为⊙O上一点,且∠A=100°,则∠BCD的度数是( )
A.40° B.140° C.100°或 40° D.40°或140°
11.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )
A.l1和l2的距离为2
B.当MN与⊙O相切时,AM=2
C.MN=
D.当∠MON=90°时,MN与⊙O相切
12.如图,点C、O在线段AB上,且AC=CO=OB=5,过点A作以BC为直径的⊙O切线,D为切点,则AD的长为( )
A.5 B.6 C. D.10
13.如图,AB是⊙O的直径,CP切⊙O于点C,交AB的延长线于点P,若∠P=20°,则∠A= .
14.如图,AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切与点D,过点B作PD的垂线,与PD的延长线相交于点C,若⊙O的半径为4,BC=6,则PA的长为 .
15.如图,PA、PB切⊙O于点A、B,AC是⊙O的直径,且∠BAC=35°,则∠P= 度.
16.如图,过⊙O外一点P作两条割线,分别交⊙O于A,B和C,D.已知PA=2,PB=5,PD=8,则PC的长是 .
17.如图,Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点为D,E,F,若AD=5,BE=12,则△ABC的周长为 .
18.如图,已知点O是△ABC的内切圆的圆心,若∠BAC=58°,则∠BOC= .
19.若一三角形的三边长分别为5、12、13,则此三角形的内切圆的面积是 .
20.如图,AB是⊙O的直径,D是弦AC延长线上一点,且AB=BD,DB的延长线交⊙O于点E,过点C作CF⊥BD,垂足为点F.
(1)CF与⊙O有怎样的位置关系?请说明理由;
(2)若BF+CF=6,⊙O的半径为5,求BE的长度.
21.如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
22.如图,AB为⊙O直径,C、D为⊙O上的点,CE⊥DB交DB的延长线于点E,且∠CBE=∠ABC.
(1)判断直线CE与⊙O的位置关系,并说明理由;
(2)求证:CD=CA;
(3)若AC=4,AB=5,求CE的长.
23.如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(1)DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
(2)若AD=4、AB=6,求直角边BC的长.
24.如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
25.如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
26.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E.过点D作⊙O的切线,交AC于点F,交AB的延长线于点G,连接DE.
(1)求证:BD=CD;
(2)若∠G=40°,求∠AED的度数.
(3)若BG=6,CF=2,求⊙O的半径.
参考答案
1.解:∵x2﹣5x﹣6=0
∴x1=﹣1,x2=6
∵⊙O的半径为一元二次方程x2﹣5x﹣6=0的根,
∴r=6
∵d<r
∴直线l与⊙O的位置关系是相交
故选:A.
2.解:在直角坐标系内,以P(2,4)为圆心,3为半径画圆,则点P到x轴的距离为d=4,
∵r=3,
∴d>r,
∴⊙P与x轴的相离.
故选:B.
3.解:连接OD,如图,
∵直线CD与⊙O相切于点D,
∴OD⊥CD,
∴∠ODC=90°,
∵CD=BD=4,
∴∠C=∠B,
∵OD=OB,
∴∠B=∠ODB,
∴∠DOE=∠B+∠ODB=2∠B,
∴∠DOE=2∠C,
在Rt△OCD中,∠DOE=2∠C,则∠DOE=60°,∠C=30°,
∴OD=cot∠EOD CD=×4=4,
∵DF⊥AB,
∴∠DEO=90°,
在Rt△ODE中,OE=cos∠EOD OD=×4=2,
故选:B.
4.解:在直角△BCM中,
tan60°==,
得到BC==2,
∵AB为圆O的直径,且AB⊥BC,
∴BC为圆O的切线,又CD也为圆O的切线,
∴CD=BC=2.
故选:C.
5.解:∵DA与△ABC的外接圆相切于点A,
∴∠CAD=∠B=60°.(弦切角定理)
故选:B.
6.解:设PA=AB=x,延长PO交圆于点D.
∵PA PB=PC PD,OC=3,OP=5,
∴x 2x=16,
∴x=2.
故选:B.
7.解:∵点P是△ABC的内心,∠BAP=50°,
∴∠BAC=2∠BAP=100°,
∴∠ABC+∠ACB=80°,
∴∠PBC+∠PCB=80°=40°,
∴∠BPC=180°﹣40°=140°,
故选:C.
8.解:∵⊙O与AB,BC,CA分别相切于点D,E,F
∴AF=AD=2,BD=BE,CE=CF,
∵△ABC的周长为14,
∴AD+AF+BE+BD+CE+CF=14
∴2(BE+CE)=10
∴BC=5
故选:C.
9.解:①当圆A在x轴的负半轴和直线y=x相切时,
由题意得,直线与x轴的交点为30°,
点A到直线的距离为1,则OA=2,
点A的坐标为(﹣2,0);
②当圆A在x轴的正半轴和直线y=x相切时,
由①得,点A的坐标为(2,0);
故选:D.
10.解:当点C在劣弧BC上时,如图1
过点B作直径BE,连接OD、DE.
∵直线AB,AD与⊙O分别相切于点B,D,
∴∠OBA=∠ODA=90°,
∵∠A=100°,
∴∠BOD=80°,
∴∠DOE=100°,
∵OD=OE,
∴∠E=50°,
∵B、C、D、E共圆,
∴∠BCD=180°﹣40°=140°,
当点C在优弧BC′D上时,如图2,∠C′=40°
故选:D.
11.解:连接OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;
作NH⊥AM于H,如图1,
则MN=AB=2,
∵∠AMN=60°,
∴sin60°=,
∴MN==;
当MN与⊙O相切,如图2,连接OM,ON,
当MN在AB左侧时,∠AMO=∠AMN=×60°=30°,
在Rt△AMO中,tan∠AMO=,即AM==,
在Rt△OBN中,∠ONB=∠BNM=60°,tan∠ONB=,即BN==,
当MN在AB右侧时,AM=,
∴AM的长为;
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.
故选:B.
12.解:∵AD是⊙O的切线,ACB是⊙O的割线,
∴AD2=AC AB,
又AC=5,AB=AC+CO+OB=15,
∴AD2=5×15=75,
∴AD=5.(AD=﹣5不合题意舍去).
故选:C.
13.解:连接OC,
∵CP切⊙O于点C,∠P=20°,
∴∠OCP=90°,
∴∠COP=70°,
∵OA=OC,
∴∠OCA=∠A=,
故答案为:35°
14.解:连接DO
解:连接DO,
∵PD与⊙O相切于点D,
∴∠PDO=90°,
∵∠C=90°,
∴DO∥BC,
∴△PDO∽△PCB,
∴
∴
∴PA=4
故答案为4
15.解:连接OB;
∵PA、PB都是⊙O的切线,且切点为A、B,
∴∠OAP=∠OBP=90°,
∴∠AOB+∠P=180°;
在△AOB中,OA=OB,∠AOB=180°﹣2∠BAC;
∴∠P=2∠BAC=70°.
16.解:∵PA PB=PC PD,PA=2,PB=5,PD=8
∴PC==.
17.解:连接EO,DO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥BC,OD⊥AC,BF=BE=12,AD=AF=5,EC=CD,
又∵∠C=90°,
∴四边形ECDO是矩形,
又∵EO=DO,
∴矩形OECD是正方形,
设EO=x,
则EC=CD=x,
在Rt△ABC中
BC2+AC2=AB2
故(x+12)2+(x+5)2=172,
解得:x=3,
∴△ABC的周长=8+15+17=40.
故答案为40.
18.解:∵点O是△ABC的内切圆的圆心,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠BAC=58°,
∴∠ABC+∠ACB=180°﹣∠BAC=122°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣×122°=119°.
故答案为:119°
19.解:∵AC2+BC2=25+144=169,AB2=169,
∴AC2+BC2=AB2,
∴∠C=90°,
连接OE、OQ,
∵圆O是三角形ABC的内切圆,
∴AE=AF,BQ=BF,∠OEC=∠OQC=∠C=90°,OE=OQ,
∴四边形OECQ是正方形,
∴设OE=CE=CQ=OQ=a,
∵AF+BF=13,
∴12﹣a+5﹣a=13,
∴a=2,
∴它的内切圆半径,
∴内切圆面积S=π r2=π×22=4π.
故答案为:4π
20.解:(1)CF与⊙O相切.连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=BD,
∴∠A=∠D,
又∵OA=OB,
∴OC是△ABD的中位线.
∴OC∥BD,
∴∠OCF=∠CFD=90°,
即CF⊥OC.
∴CF与⊙O相切;
(2)过点O作OH⊥BE于点H,则∠OCF=∠CFH=∠OHB=90°,
∴四边形OCFH是矩形,
∴OC=FH,OH=CF,
设BH=x,
∵OC=5,BF+CF=6,
∴BF=5﹣x,OH=CF=6﹣(5﹣x)=x+1,
在Rt△BOH中,由勾股定理知:
BH2+OH2=OB2,即x2+(x+1)2=52,
解得x1=3,x2=﹣4(不合题意,舍去).
∴BH=3,
∵OH⊥BE,
∴BH=EH=BE,
∴BE=2BH=2×3=6.
21.解:(1)连接BD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD==5,
在Rt△ACB中,AB=10,BC=5,
∴AC==5,
答:AC=5,AD=5;
(2)直线PC与⊙O相切,理由是:
连接OC,
在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠COB=60°,
∵∠ACD=45°,
∴∠OCD=45°﹣30°=15°,
∴∠CEP=∠COB+∠OCD=15°+60°=75°,
∵PC=PE,
∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与⊙O相切.
22.解:(1)直线CE与⊙O相切,
理由:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥DB,
∴∠E=90°,
∵∠CBE=∠ABC,
∴∠ECB=∠A,
∵OC=OA,
∴∠A=∠ACO,
∵∠ACO+∠OCB=90°,
∴∠ECB+∠OCB=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)连接AD,
∵AB为⊙O直径,
∴AD⊥DE,
∵CE⊥DE,
∴CE∥AD,
∴∠ECD=∠ADC,
∵CE是⊙O的切线,
∴∠CAD=∠ECD,
∴∠CAD=∠ADC,
∴AC=CD;
(3)∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ACB中,AC=4,AB=5,
∴BC==3,
∵∠CAB=∠∠CDB,
∴Rt△ACB∽Rt△DEC,
∴=,即=,
∴EC=.
23.解:(1)连OD,OE,如图,
∵E是BC边上的中点,AB是半圆O的直径,
∴OE是△ABC的中位线,
∴OE∥AC,
∴∠1=∠3,∠2=∠A,而OD=OA,∠A=∠3,
∴∠1=∠2,
又∵OD=OB,OE为公共边,
∴△OED≌△OEB,
∴∠ODE=∠OBE=90°.
∴DE与半圆O相切.
(2)∵AB为直径
∴∠ADB=∠ABC=90°,
∴∠CAB=∠CAB,
∴△ABC∽△ADB.
∴,
∵AD=4、AB=6,
∴AC=9,
∴在Rt△ABC中:BC===3.
24.(1)证明:连接OD,如图所示:
∵OD=OB,
∴∠1=∠2,
又∵BD平分∠ABC,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥BC,
而∠C=90°,
∴OD⊥AD,
∴AC与⊙O相切于D点;
(2)解:∵OD⊥AD,
∴在RT△OAD中,OA2=OD2+AD2,
又∵AD=15,AE=9,设半径为r,
∴(r+9)2=152+r2,
解方程得,r=8,
即⊙O的半径为8.
25.解:(1)如图连接OD.
∵BD是⊙O的切线,
∴OD⊥BD.
∵AC⊥BD,
∴OD∥AC.
∴∠ODA=∠DAC.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD,即AD平分∠BAC.
(2)OD∥AC,
∴△BOD∽△BAC,
∴=,即=,解得:AC=.
26.(1)证明:连接AD,
∵AB为直径,
∴∠ACB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)解:连接OD,
∵GF是切线,OD是半径,
∴OD⊥GF,
∴∠ODG=90°,
∵∠G=40°,
∴∠GOD=50°,
∵OB=OD,
∴∠OBD=65°,
∵点A、B、D、E都在⊙O上,
∴∠ABD+∠AED=180°,
∴∠AED=115°;
(3)解:∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△GOD∽△GAF,
∴=,
∴设⊙O的半径是r,则AB=AC=2r,
∴AF=2r﹣2,
∴=,
∴r=3,
即⊙O的半径是3.
