2021-2022学年人教版九年级数学上册24.4弧长和扇形面积同步培优练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.4弧长和扇形面积同步培优练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 570.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 18:22:06 | ||
图片预览




文档简介
人教版 九年级数学上册 24.4 弧长和扇形面积 同步培优
一、选择题
1. 2019·湖州已知圆锥的底面半径为5 cm,母线长为13 cm,则这个圆锥的侧面积是( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
2. 2019·天水模拟 一个圆锥的轴截面是一个正三角形,则圆锥侧面展开图形的圆心角是( )
A.60° B.90° C.120° D.180°
3. (2020·达州)如图,在半径为5的⊙O中,将劣弧AB沿弦AB翻折,使折叠后的弧AB恰好与OA、OB相切,则劣弧AB的长为( )
A. B. C. D.
4. 小明用图中的扇形纸片作一个圆锥的侧面.已知该扇形的半径是5 cm,弧长是6π cm,那么这个圆锥的高是( )
A.4 cm B.6 cm C.8 cm D.12 cm
5. 如图,在Rt△ABC中,∠ACB=90°,AC=2,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
A. 2-π B. 4-π C. 2-π D. π
6. (2020 遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4﹣ B.2﹣ C.2﹣π D.1﹣
二、填空题
7. 如图,在⊙O中,∠AOB=60°,AB=3 cm,则劣弧的长为________ cm.
8. (2020·湘潭)如图,在半径为6的⊙O中,圆心角,则阴影部分面积为________.
9. (2020·温州)若扇形的圆心角为45°,半径为3,则该扇形的弧长为 .
10. 【题目】(2020·营口)一个圆锥的底面半径为3,高为4,则此圆锥的侧面积为 .
11. 如图,把一个圆锥沿母线OA剪开,展开后得到扇形OAC.已知圆锥的高h为12 cm,OA=13 cm,则扇形OAC中的长是________ cm.(结果保留π)
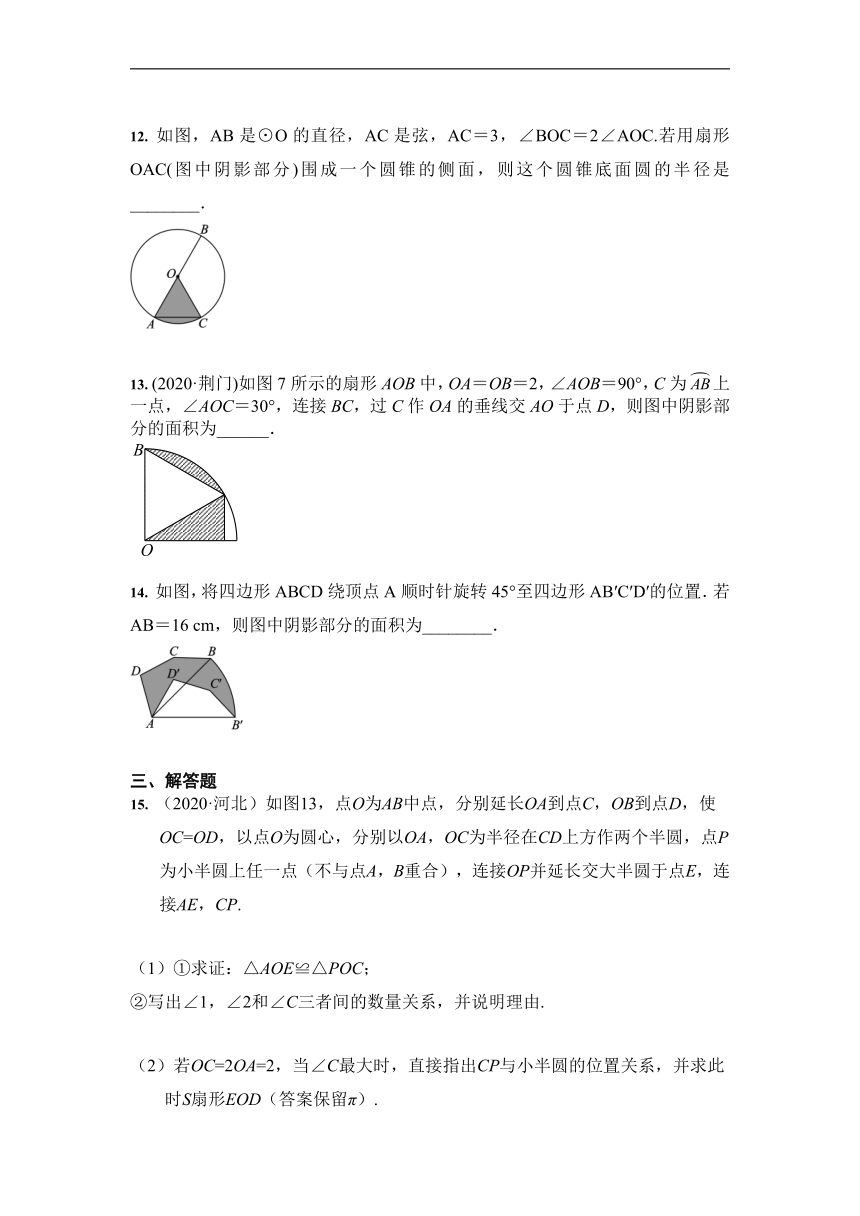
12. 如图,AB是⊙O的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是________.
13. (2020·荆门)如图7所示的扇形AOB中,OA=OB=2,∠AOB=90°,C为上一点,∠AOC=30°,连接BC,过C作OA的垂线交AO于点D,则图中阴影部分的面积为______.
14. 如图,将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置.若AB=16 cm,则图中阴影部分的面积为________.
三、解答题
15. (2020·河北)如图13,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD,以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆,点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)①求证:△AOE≌△POC;
②写出∠1,∠2和∠C三者间的数量关系,并说明理由.
(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).
16. 一个圆锥的高为3 ,侧面展开图半圆,求:
(1)圆锥的母线长与底面圆半径的比;
(2)圆锥的全面积.
17. 已知扇形的圆心角为120°,面积为300π cm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的体积是多少?
18. 如图所示的粮囤可以看成是圆柱体与圆锥体的组合体,已知其底面圆的半径为6 m,高为4 m,下方圆柱的高为3 m.
(1)求该粮囤的容积;
(2)求上方圆锥的侧面积(计算结果保留根号).
19. 当汽车在雨天行驶时,司机为了看清楚道路,要启动前方挡风玻璃上的雨刷.如图是某汽车的一个雨刷的转动示意图,雨刷杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕点A转动90°时,雨刷CD扫过的面积是图中阴影部分的面积,现量得CD=90 cm,∠DBA=20°,AC=115 cm,DA=35 cm,试从以上信息中选择所需要的数据,求出雨刷扫过的面积.
20. 如图,PB切⊙O于点B,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为D,交⊙O于点A,连接AO并延长交⊙O于点C,连接BC,AF,BF.
(1)若∠AOF=120°,⊙O的半径为3,
求:①∠CBF的度数;
②的长;
③阴影部分的面积.
(2)若AB=8,DE=2,求⊙O的半径.
(3)求证:直线PA为⊙O的切线.
(4)若BC=6,AD∶FD=1∶2,求⊙O的半径.
人教版 九年级数学上册 24.4 弧长和扇形面积 同步培优-答案
一、选择题
1. 【答案】B [解析] ∵r=5 cm,l=13 cm,∴S圆锥侧=πrl=π×5×13=65π(cm2).故选B.
2. 【答案】D
3. 【答案】B
【解析】由“折叠后的弧AB恰好与OA、OB相切”可知:∠OAB=∠OBA=45°,所以∠AOB=90°,劣弧AB的长=.
4. 【答案】A [解析] 设圆锥的底面圆的半径是r cm,则2πr=6π,解得r=3,则圆锥的高是=4(cm).
5. 【答案】A 【解析】设BC=x,∵D为AB的中点,∴AB=2BC=2x, ∴在Rt△ABC中,由勾股定理有(2x)2-x2=(2)2,解得x=2,又∵sinA==, ∴∠A=30°,∠B=60°,∴S阴影=S△ABC-S扇形BCD=×2×2-=2-π.
6. 【答案】连接OD,过O作OH⊥AC于H,如图,
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵⊙O与BC相切于点D,
∴OD⊥BC,
∴四边形ODCH为矩形,
∴OH=CD=,
在Rt△OAH中,∠OAH=45°,
∴OA=OH=2,
在Rt△OBD中,∵∠B=45°,
∴∠BOD=45°,BD=OD=2,
∴图中阴影部分面积=S△OBD﹣S扇形DOE
=×2×2﹣
=2﹣π.
故选:B.
二、填空题
7. 【答案】π 【解析】由OA=OB,∠AOB=60°.可得△AOB为等边三角形,∴⊙O的半径OA=AB=3 cm,∴l=×π×3=π(cm).
8. 【答案】
【解析】本题考查了扇形面积的计算,解题的关键是熟记扇形面积的计算公式.
阴影部分面积为,
故答案为:.
9. 【答案】
【解析】本题考查了弧长公式.∵n=45°,r=3,∴,因此本题答案为.
10. 【答案】
【解析】在圆锥中,底面半径r,高h,母线长l满足r2+h2=l2,因为r=3,h=4,可求得l=5(负值舍去).而圆锥的侧面积公式是S侧=rl,所以上述圆锥侧面积为×3×5=15.
11. 【答案】10π [解析] 由勾股定理,得圆锥的底面圆半径为=5(cm),∴扇形的弧长=圆锥的底面圆周长=2π×5=10π(cm).
12. 【答案】 [解析] 设这个圆锥底面圆的半径是r.
∵∠BOC=2∠AOC,∠BOC+∠AOC=180°,
∴∠AOC=60°.
又∵OA=OC,∴△OAC为等边三角形,
∴OA=OC=AC=3,∴l==2πr,
解得r=,
∴这个圆锥底面圆的半径是.
13. 【答案】π-
【解析】∵OC=OA=2,∠AOC=30°,∴∠BOC=60°,CD=1,OD=.∴S阴影=S△OCD+S弓BC=××1+-×22=π-.
14. 【答案】32π cm2 [解析] 由旋转的性质得∠BAB′=45°,四边形AB′C′D′≌四边形ABCD,
则图中阴影部分的面积=四边形ABCD的面积+扇形ABB′的面积-四边形AB′C′D′的面积=扇形ABB′的面积==32π(cm2).
三、解答题
15. 【答案】
解:解:(1)①证明:∵OA=OB,OE=OC,∠AOE=∠POC,∴△AOE≌△POC;
②∠1+∠C=∠2.理由:∵△AOE≌△POC,∴∠E=∠C.∵∠1+∠E=∠2,∴∠1+∠C=∠2.
(2)相切.
如图,∵CP与小半圆相切,∴CP⊥OP.
在Rt△OPC中,∵OP=1,OC=2,∴cos∠COP=,∴∠COP=60°.
∴∠DOE=120°.∴S扇形EOD=.
【解析】本题考查了平行四边形的性质、垂直的性质、三角形内角和定理、平行线的性质和全等三角形的判定和性质等知识.(1)在△AOE中,由∠AEO和∠AOE的度数求得∠EAO的度数,再由AC平分∠DAE求得∠OAD的度数,进而由AD∥BC得到∠ACB=∠OAD,问题得解;(2)先根据AAS证明△AEO≌△CFO,再根据相似三角形对应边相等得到AE=CF.
16. 【答案】
解:(1)设圆锥的母线长为l,底面圆的半径为r,
根据题意得2πr=,
所以l=2r,
即圆锥的母线长与底面圆半径的比为2∶1.
(2)因为r2+(3 )2=l2,
即r2+(3 )2=4r2,解得r=3(负值已舍去),
所以l=6,
所以圆锥的全面积=π·32+·2π·3·6=27π.
17. 【答案】
证明:如图,连接AD,OC.
∵OD⊥AC,∴AE=EC.
由翻折的性质,得AC是OD的垂直平分线,
∴OE=DE,
∴四边形OADC是平行四边形,
∴OA∥CD,OA=CD.
∵OA=OB,∴OB=CD,OB∥CD,
∴四边形BCDO是平行四边形.
又∵OB=OD,
∴四边形BCDO是菱形.
18. 【答案】
解:(1)证明:∵CD⊥AB,CD是⊙O的直径,
∴=,
∴∠AEC=∠BEC,
∴EC平分∠AEB.
(2)∵CD⊥AB,
∴BG=AG=AB=3,∠BGC=90°.
在Rt△BGC中,
∵CG=4,BG=3,
∴BC=5.
∵BC∥AE,
∴∠AEC=∠BCE.
又∵∠AEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC=5.
19. 【答案】
解: 如图,过点O作OG⊥AP于点G,连接OF.
∵DB=10 cm,
∴OD=OF=5 cm,
∴AO=AD+OD=3+5=8(cm).
∵∠PAC=30°,
∴OG=AO=×8=4(cm).
∵OG⊥EF,∴EG=GF=EF.
∵GF===3(cm),
∴EF=2GF=6 cm,
∴圆心O到AP的距离为4 cm,EF的长为6 cm.
20. 【答案】
解:P为半圆的中点.
证明:如图,连接OP.
∵∠OCD的平分线交⊙O于点P,∴∠PCD=∠PCO.
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD.
∵CD⊥AB,∴OP⊥AB,
∴=,即P为半圆的中点.
D
C
A
B
O
图7
一、选择题
1. 2019·湖州已知圆锥的底面半径为5 cm,母线长为13 cm,则这个圆锥的侧面积是( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
2. 2019·天水模拟 一个圆锥的轴截面是一个正三角形,则圆锥侧面展开图形的圆心角是( )
A.60° B.90° C.120° D.180°
3. (2020·达州)如图,在半径为5的⊙O中,将劣弧AB沿弦AB翻折,使折叠后的弧AB恰好与OA、OB相切,则劣弧AB的长为( )
A. B. C. D.
4. 小明用图中的扇形纸片作一个圆锥的侧面.已知该扇形的半径是5 cm,弧长是6π cm,那么这个圆锥的高是( )
A.4 cm B.6 cm C.8 cm D.12 cm
5. 如图,在Rt△ABC中,∠ACB=90°,AC=2,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
A. 2-π B. 4-π C. 2-π D. π
6. (2020 遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4﹣ B.2﹣ C.2﹣π D.1﹣
二、填空题
7. 如图,在⊙O中,∠AOB=60°,AB=3 cm,则劣弧的长为________ cm.
8. (2020·湘潭)如图,在半径为6的⊙O中,圆心角,则阴影部分面积为________.
9. (2020·温州)若扇形的圆心角为45°,半径为3,则该扇形的弧长为 .
10. 【题目】(2020·营口)一个圆锥的底面半径为3,高为4,则此圆锥的侧面积为 .
11. 如图,把一个圆锥沿母线OA剪开,展开后得到扇形OAC.已知圆锥的高h为12 cm,OA=13 cm,则扇形OAC中的长是________ cm.(结果保留π)
12. 如图,AB是⊙O的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是________.
13. (2020·荆门)如图7所示的扇形AOB中,OA=OB=2,∠AOB=90°,C为上一点,∠AOC=30°,连接BC,过C作OA的垂线交AO于点D,则图中阴影部分的面积为______.
14. 如图,将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置.若AB=16 cm,则图中阴影部分的面积为________.
三、解答题
15. (2020·河北)如图13,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD,以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆,点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)①求证:△AOE≌△POC;
②写出∠1,∠2和∠C三者间的数量关系,并说明理由.
(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).
16. 一个圆锥的高为3 ,侧面展开图半圆,求:
(1)圆锥的母线长与底面圆半径的比;
(2)圆锥的全面积.
17. 已知扇形的圆心角为120°,面积为300π cm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的体积是多少?
18. 如图所示的粮囤可以看成是圆柱体与圆锥体的组合体,已知其底面圆的半径为6 m,高为4 m,下方圆柱的高为3 m.
(1)求该粮囤的容积;
(2)求上方圆锥的侧面积(计算结果保留根号).
19. 当汽车在雨天行驶时,司机为了看清楚道路,要启动前方挡风玻璃上的雨刷.如图是某汽车的一个雨刷的转动示意图,雨刷杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕点A转动90°时,雨刷CD扫过的面积是图中阴影部分的面积,现量得CD=90 cm,∠DBA=20°,AC=115 cm,DA=35 cm,试从以上信息中选择所需要的数据,求出雨刷扫过的面积.
20. 如图,PB切⊙O于点B,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为D,交⊙O于点A,连接AO并延长交⊙O于点C,连接BC,AF,BF.
(1)若∠AOF=120°,⊙O的半径为3,
求:①∠CBF的度数;
②的长;
③阴影部分的面积.
(2)若AB=8,DE=2,求⊙O的半径.
(3)求证:直线PA为⊙O的切线.
(4)若BC=6,AD∶FD=1∶2,求⊙O的半径.
人教版 九年级数学上册 24.4 弧长和扇形面积 同步培优-答案
一、选择题
1. 【答案】B [解析] ∵r=5 cm,l=13 cm,∴S圆锥侧=πrl=π×5×13=65π(cm2).故选B.
2. 【答案】D
3. 【答案】B
【解析】由“折叠后的弧AB恰好与OA、OB相切”可知:∠OAB=∠OBA=45°,所以∠AOB=90°,劣弧AB的长=.
4. 【答案】A [解析] 设圆锥的底面圆的半径是r cm,则2πr=6π,解得r=3,则圆锥的高是=4(cm).
5. 【答案】A 【解析】设BC=x,∵D为AB的中点,∴AB=2BC=2x, ∴在Rt△ABC中,由勾股定理有(2x)2-x2=(2)2,解得x=2,又∵sinA==, ∴∠A=30°,∠B=60°,∴S阴影=S△ABC-S扇形BCD=×2×2-=2-π.
6. 【答案】连接OD,过O作OH⊥AC于H,如图,
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵⊙O与BC相切于点D,
∴OD⊥BC,
∴四边形ODCH为矩形,
∴OH=CD=,
在Rt△OAH中,∠OAH=45°,
∴OA=OH=2,
在Rt△OBD中,∵∠B=45°,
∴∠BOD=45°,BD=OD=2,
∴图中阴影部分面积=S△OBD﹣S扇形DOE
=×2×2﹣
=2﹣π.
故选:B.
二、填空题
7. 【答案】π 【解析】由OA=OB,∠AOB=60°.可得△AOB为等边三角形,∴⊙O的半径OA=AB=3 cm,∴l=×π×3=π(cm).
8. 【答案】
【解析】本题考查了扇形面积的计算,解题的关键是熟记扇形面积的计算公式.
阴影部分面积为,
故答案为:.
9. 【答案】
【解析】本题考查了弧长公式.∵n=45°,r=3,∴,因此本题答案为.
10. 【答案】
【解析】在圆锥中,底面半径r,高h,母线长l满足r2+h2=l2,因为r=3,h=4,可求得l=5(负值舍去).而圆锥的侧面积公式是S侧=rl,所以上述圆锥侧面积为×3×5=15.
11. 【答案】10π [解析] 由勾股定理,得圆锥的底面圆半径为=5(cm),∴扇形的弧长=圆锥的底面圆周长=2π×5=10π(cm).
12. 【答案】 [解析] 设这个圆锥底面圆的半径是r.
∵∠BOC=2∠AOC,∠BOC+∠AOC=180°,
∴∠AOC=60°.
又∵OA=OC,∴△OAC为等边三角形,
∴OA=OC=AC=3,∴l==2πr,
解得r=,
∴这个圆锥底面圆的半径是.
13. 【答案】π-
【解析】∵OC=OA=2,∠AOC=30°,∴∠BOC=60°,CD=1,OD=.∴S阴影=S△OCD+S弓BC=××1+-×22=π-.
14. 【答案】32π cm2 [解析] 由旋转的性质得∠BAB′=45°,四边形AB′C′D′≌四边形ABCD,
则图中阴影部分的面积=四边形ABCD的面积+扇形ABB′的面积-四边形AB′C′D′的面积=扇形ABB′的面积==32π(cm2).
三、解答题
15. 【答案】
解:解:(1)①证明:∵OA=OB,OE=OC,∠AOE=∠POC,∴△AOE≌△POC;
②∠1+∠C=∠2.理由:∵△AOE≌△POC,∴∠E=∠C.∵∠1+∠E=∠2,∴∠1+∠C=∠2.
(2)相切.
如图,∵CP与小半圆相切,∴CP⊥OP.
在Rt△OPC中,∵OP=1,OC=2,∴cos∠COP=,∴∠COP=60°.
∴∠DOE=120°.∴S扇形EOD=.
【解析】本题考查了平行四边形的性质、垂直的性质、三角形内角和定理、平行线的性质和全等三角形的判定和性质等知识.(1)在△AOE中,由∠AEO和∠AOE的度数求得∠EAO的度数,再由AC平分∠DAE求得∠OAD的度数,进而由AD∥BC得到∠ACB=∠OAD,问题得解;(2)先根据AAS证明△AEO≌△CFO,再根据相似三角形对应边相等得到AE=CF.
16. 【答案】
解:(1)设圆锥的母线长为l,底面圆的半径为r,
根据题意得2πr=,
所以l=2r,
即圆锥的母线长与底面圆半径的比为2∶1.
(2)因为r2+(3 )2=l2,
即r2+(3 )2=4r2,解得r=3(负值已舍去),
所以l=6,
所以圆锥的全面积=π·32+·2π·3·6=27π.
17. 【答案】
证明:如图,连接AD,OC.
∵OD⊥AC,∴AE=EC.
由翻折的性质,得AC是OD的垂直平分线,
∴OE=DE,
∴四边形OADC是平行四边形,
∴OA∥CD,OA=CD.
∵OA=OB,∴OB=CD,OB∥CD,
∴四边形BCDO是平行四边形.
又∵OB=OD,
∴四边形BCDO是菱形.
18. 【答案】
解:(1)证明:∵CD⊥AB,CD是⊙O的直径,
∴=,
∴∠AEC=∠BEC,
∴EC平分∠AEB.
(2)∵CD⊥AB,
∴BG=AG=AB=3,∠BGC=90°.
在Rt△BGC中,
∵CG=4,BG=3,
∴BC=5.
∵BC∥AE,
∴∠AEC=∠BCE.
又∵∠AEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC=5.
19. 【答案】
解: 如图,过点O作OG⊥AP于点G,连接OF.
∵DB=10 cm,
∴OD=OF=5 cm,
∴AO=AD+OD=3+5=8(cm).
∵∠PAC=30°,
∴OG=AO=×8=4(cm).
∵OG⊥EF,∴EG=GF=EF.
∵GF===3(cm),
∴EF=2GF=6 cm,
∴圆心O到AP的距离为4 cm,EF的长为6 cm.
20. 【答案】
解:P为半圆的中点.
证明:如图,连接OP.
∵∠OCD的平分线交⊙O于点P,∴∠PCD=∠PCO.
∵OC=OP,∴∠PCO=∠OPC,
∴∠PCD=∠OPC,∴OP∥CD.
∵CD⊥AB,∴OP⊥AB,
∴=,即P为半圆的中点.
D
C
A
B
O
图7
同课章节目录
