2021-2022学年北师大版九年级数学下册第3章圆 期末综合复习题(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章圆 期末综合复习题(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 461.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 18:30:43 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》期末综合复习题(附答案)
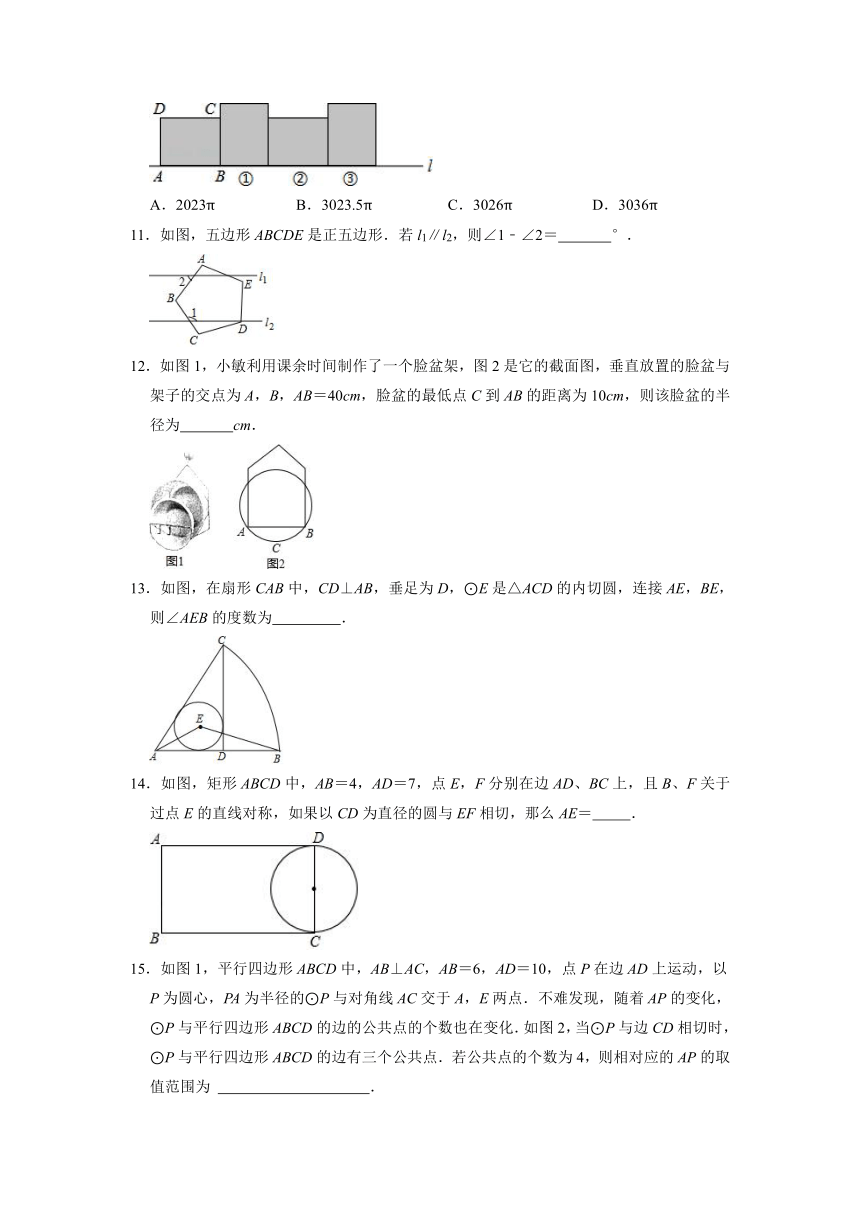
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
2.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
3.如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A.DE=EB B.DE=EB C.DE=DO D.DE=OB
4.过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
5.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
6.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
A.﹣2﹣ B.﹣2+ C.+ D.﹣
7.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
A.2.5 B.2.8 C.3 D.3.2
8.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB的长为( )
A.15 B. C.13 D.
9.如图,直线l:y=﹣x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,m的值为( )
A.4或﹣4 B.4﹣或4+ C.﹣4+或4+ D.4﹣或4+
10.如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2023次后,顶点A在整个旋转过程中所经过的路程之和是( )
A.2023π B.3023.5π C.3026π D.3036π
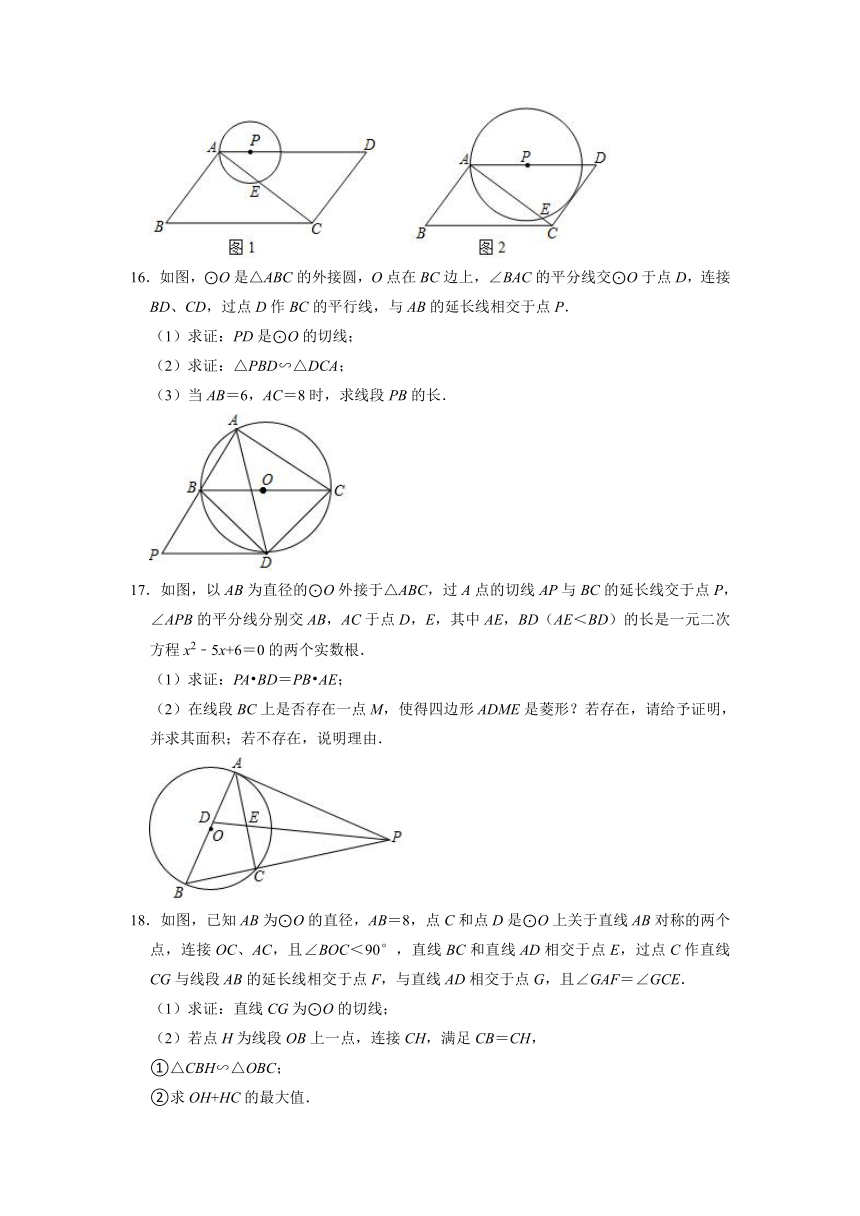
11.如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2= °.
12.如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
13.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .
14.如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= .
15.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
16.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
17.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PA BD=PB AE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
18.如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC;
②求OH+HC的最大值.
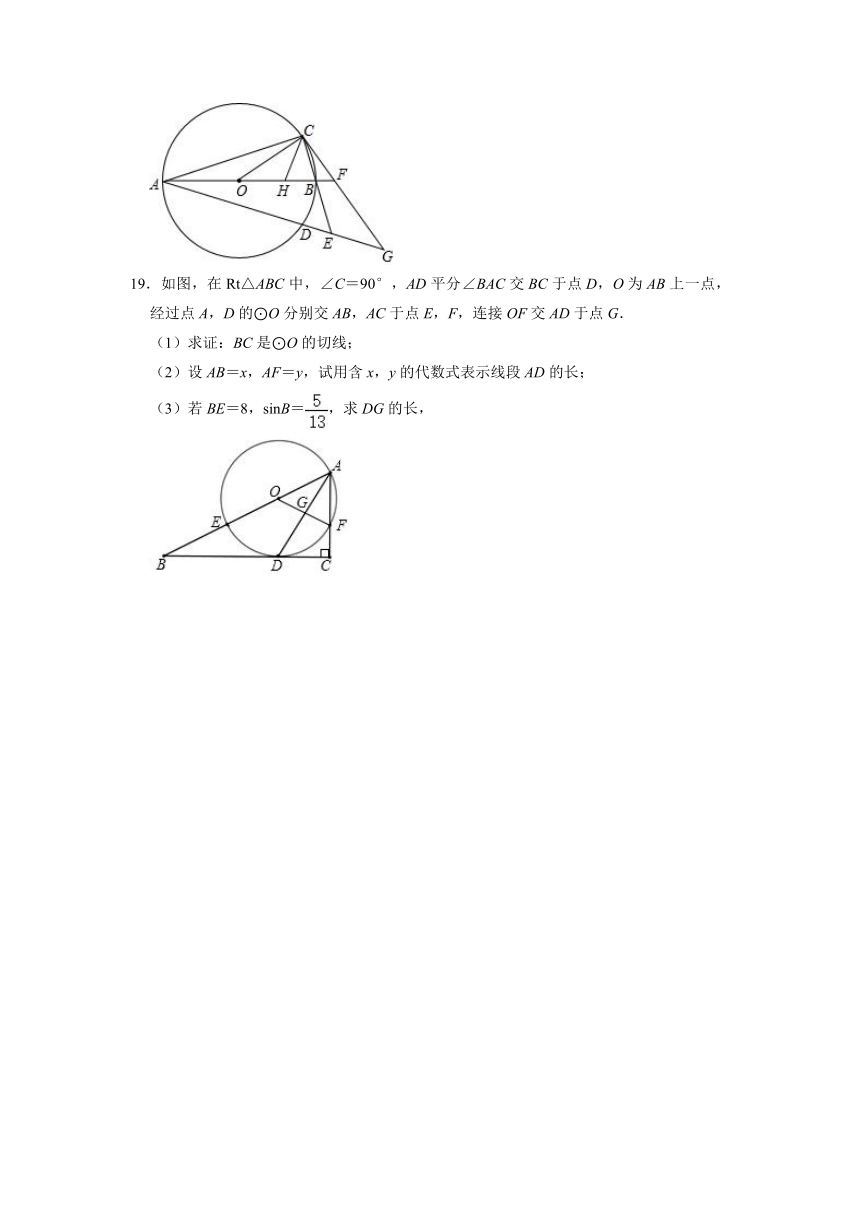
19.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长,
参考答案
1.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,=,=,
∴∠ACD=∠ADC.
故选:D.
2.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠ADC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选:C.
3.解:连接EO.
∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选:D.
4.解:如图,设△ABC的外心E(4,t),则CE=5﹣t,EM=t﹣2,
∵EC=AE,
∴5﹣t=,
解得t=,可得结论.
故选:A.
5.解:连接DO,
∵PD与⊙O相切于点D,
∴∠PDO=90°,
∵∠C=90°,
∴DO∥BC,
∴△PDO∽△PCB,
∴===,
设PA=x,则=,
解得:x=4,
故PA=4.
故选:A.
6.解:连接DC1,
∵∠CAC1=∠DCA=∠COB1=∠DOC1=45°,
∴∠AC1B1=45°,
∵∠ADC=90°,
∴A,D,C1在一条直线上,
∵四边形ABCD是正方形,
∴AC=,∠OCB1=45°,
∴CB1=OB1
∵AB1=1,
∴CB1=OB1=AC﹣AB1=﹣1,
∴S△OB1C= OB1 CB1=(﹣1)2,
∵S△AB1C1=AB1 B1C1=×1×1=,
∴图中阴影部分的面积=﹣(﹣1)2﹣=﹣2+.
故选:B.
7.解:如图1,连接BD、CD,
,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=,
∵弦AD平分∠BAC,
∴CD=BD=,
∴∠CBD=∠DAB,
在△ABD和△BED中,
∴△ABD∽△BED,
∴=,即=,
解得DE=,
∴AE=AD﹣DE=5﹣=2.8.
故选:B.
8.解:如图,作直径AE,连接CE,
∴∠ACE=90°,
∵AH⊥BC,
∴∠AHB=90°,
∴∠ACE=∠AHB,
∵∠E=∠B,
∴△ACE∽△AHB,
∴=,
∴AB=,
∵AC=24,AH=18,AE=2OC=26,
∴AB==.
则AB的长为 .
故选:B.
9.解:在y=﹣x+1中,
令x=0,则y=1,
令y=0,则x=,
∴A(0,1),B(,0),
∴AB=2;
如图,设⊙M与AB相切与C,
连接MC,则MC=2,MC⊥AB,
∵∠MCB=∠AOB=90°,∠ABO=∠CBM,
∴△BMC∽△BAO,
∴=,即=,
∴BM=4,
∴OM=4﹣,或OM=4+.
∴m=﹣4,m=4+.
故选:C.
10.解:转动一次A的路线长是:,
转动第二次的路线长是:,
转动第三次的路线长是:,
转动第四次的路线长是:0,
转动五次A的路线长是:,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为:+2π=6π,
2023÷4=505余3
顶点A转动2023次经过的路线长为:6π×506=3036π.
故选:D.
11.解:过B点作BF∥l1,
∵五边形ABCDE是正五边形,
∴∠ABC=108°,
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠3=180°﹣∠1,∠4=∠2,
∴180°﹣∠1+∠2=∠ABC=108°,
∴∠1﹣∠2=72°.
故答案为:72.
12.解;如图,设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,
∵OC⊥AB,
∴AD=DB=AB=20,∠ADO=90°,
在RT△AOD中,∵OA2=OD2+AD2,
∴R2=202+(R﹣10)2,
∴R=25.
故答案为25.
13.解:如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180°﹣(∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
14.解:如图,设⊙O与EF相切于M,连接EB,作EH⊥BC于H.
由题意易知四边形AEHB是矩形,设AE=BH=x,
由切线长定理可知,ED=EM,FC=FM,
∵B、F关于EH对称,
∴HF=BH=x,ED=EM=7﹣x,FC=FM=7﹣2x,EF=14﹣3x,
在Rt△EFH中,∵EF2=EH2+HF2,
∴42+x2=(14﹣3x)2,
解得x=3或(舍弃),
∴AE=3,
故答案为3.
15.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
16.(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)证明:∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,
∴BC2=AB2+AC2=62+82=100,
∴BC=10,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,
∴DC=DB=5,
∵△PBD∽△DCA,
∴=,
则PB===.
17.解:(1)证明:∵DP平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴,
∴PA BD=PB AE;
(2)在线段BC上存在一点M,使得四边形ADME是菱形,
证明:过点D作DF⊥PB于点F,作DG⊥AC于点G,连接EF,
∵DP平分∠APB,
AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0,
解得:AE=2,BD=3,
∴由(1)可知:,
∴cos∠APC==,
∴cos∠BDF=cos∠APC=,
∴,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=AE,
∴四边形ADFE是菱形,
此时点F即为M点,
∵cos∠BAC=cos∠APC=,
∴sin∠BAC=,
∴,
∴DG=,
∴在线段BC上存在一点M,使得四边形ADME是菱形,
其面积为:DG AE=2×=.
18.解:(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线;
(2)①∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC
②由△CBH∽△OBC可知:
∵AB=8,
∴BC2=HB OC=4HB,
∴HB=,
∴OH=OB﹣HB=4﹣
∵CB=CH,
∴OH+HC=4+BC,
当∠BOC=90°,
此时BC=4
∵∠BOC<90°,
∴0<BC<4,
令BC=x
∴OH+HC=﹣(x﹣2)2+5
当x=2时,
∴OH+HC可取得最大值,最大值为5
19.(1)证明:如图,连接OD,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
∴OD⊥BC,
∴BC为圆O的切线;
(2)解:连接DF,由(1)知BC为圆O的切线,
∴∠FDC=∠DAF,
∴∠CDA=∠CFD,
∴∠AFD=∠ADB,
∵∠BAD=∠DAF,
∴△ABD∽△ADF,
∴=,即AD2=AB AF=xy,
则AD=;
(3)解:连接EF,在Rt△BOD中,sinB==,
设圆的半径为r,可得=,
解得:r=5,
∴AE=10,AB=18,
∵AE是直径,
∴∠AFE=∠C=90°,
∴EF∥BC,
∴∠AEF=∠B,
∴sin∠AEF==,
∴AF=AE sin∠AEF=10×=,
∵AF∥OD,
∴===,即DG=AD,
∴AD===,
则DG=×=.
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
2.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
3.如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
A.DE=EB B.DE=EB C.DE=DO D.DE=OB
4.过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
A.(4,) B.(4,3) C.(5,) D.(5,3)
5.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
6.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
A.﹣2﹣ B.﹣2+ C.+ D.﹣
7.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
A.2.5 B.2.8 C.3 D.3.2
8.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB的长为( )
A.15 B. C.13 D.
9.如图,直线l:y=﹣x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,m的值为( )
A.4或﹣4 B.4﹣或4+ C.﹣4+或4+ D.4﹣或4+
10.如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2023次后,顶点A在整个旋转过程中所经过的路程之和是( )
A.2023π B.3023.5π C.3026π D.3036π
11.如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2= °.
12.如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
13.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .
14.如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= .
15.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为 .
16.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.
17.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PA BD=PB AE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
18.如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC;
②求OH+HC的最大值.
19.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长,
参考答案
1.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,=,=,
∴∠ACD=∠ADC.
故选:D.
2.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠ADC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选:C.
3.解:连接EO.
∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选:D.
4.解:如图,设△ABC的外心E(4,t),则CE=5﹣t,EM=t﹣2,
∵EC=AE,
∴5﹣t=,
解得t=,可得结论.
故选:A.
5.解:连接DO,
∵PD与⊙O相切于点D,
∴∠PDO=90°,
∵∠C=90°,
∴DO∥BC,
∴△PDO∽△PCB,
∴===,
设PA=x,则=,
解得:x=4,
故PA=4.
故选:A.
6.解:连接DC1,
∵∠CAC1=∠DCA=∠COB1=∠DOC1=45°,
∴∠AC1B1=45°,
∵∠ADC=90°,
∴A,D,C1在一条直线上,
∵四边形ABCD是正方形,
∴AC=,∠OCB1=45°,
∴CB1=OB1
∵AB1=1,
∴CB1=OB1=AC﹣AB1=﹣1,
∴S△OB1C= OB1 CB1=(﹣1)2,
∵S△AB1C1=AB1 B1C1=×1×1=,
∴图中阴影部分的面积=﹣(﹣1)2﹣=﹣2+.
故选:B.
7.解:如图1,连接BD、CD,
,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=,
∵弦AD平分∠BAC,
∴CD=BD=,
∴∠CBD=∠DAB,
在△ABD和△BED中,
∴△ABD∽△BED,
∴=,即=,
解得DE=,
∴AE=AD﹣DE=5﹣=2.8.
故选:B.
8.解:如图,作直径AE,连接CE,
∴∠ACE=90°,
∵AH⊥BC,
∴∠AHB=90°,
∴∠ACE=∠AHB,
∵∠E=∠B,
∴△ACE∽△AHB,
∴=,
∴AB=,
∵AC=24,AH=18,AE=2OC=26,
∴AB==.
则AB的长为 .
故选:B.
9.解:在y=﹣x+1中,
令x=0,则y=1,
令y=0,则x=,
∴A(0,1),B(,0),
∴AB=2;
如图,设⊙M与AB相切与C,
连接MC,则MC=2,MC⊥AB,
∵∠MCB=∠AOB=90°,∠ABO=∠CBM,
∴△BMC∽△BAO,
∴=,即=,
∴BM=4,
∴OM=4﹣,或OM=4+.
∴m=﹣4,m=4+.
故选:C.
10.解:转动一次A的路线长是:,
转动第二次的路线长是:,
转动第三次的路线长是:,
转动第四次的路线长是:0,
转动五次A的路线长是:,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为:+2π=6π,
2023÷4=505余3
顶点A转动2023次经过的路线长为:6π×506=3036π.
故选:D.
11.解:过B点作BF∥l1,
∵五边形ABCDE是正五边形,
∴∠ABC=108°,
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠3=180°﹣∠1,∠4=∠2,
∴180°﹣∠1+∠2=∠ABC=108°,
∴∠1﹣∠2=72°.
故答案为:72.
12.解;如图,设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,
∵OC⊥AB,
∴AD=DB=AB=20,∠ADO=90°,
在RT△AOD中,∵OA2=OD2+AD2,
∴R2=202+(R﹣10)2,
∴R=25.
故答案为25.
13.解:如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180°﹣(∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
14.解:如图,设⊙O与EF相切于M,连接EB,作EH⊥BC于H.
由题意易知四边形AEHB是矩形,设AE=BH=x,
由切线长定理可知,ED=EM,FC=FM,
∵B、F关于EH对称,
∴HF=BH=x,ED=EM=7﹣x,FC=FM=7﹣2x,EF=14﹣3x,
在Rt△EFH中,∵EF2=EH2+HF2,
∴42+x2=(14﹣3x)2,
解得x=3或(舍弃),
∴AE=3,
故答案为3.
15.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
16.(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)证明:∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
(3)解:∵△ABC为直角三角形,
∴BC2=AB2+AC2=62+82=100,
∴BC=10,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=100,
∴DC=DB=5,
∵△PBD∽△DCA,
∴=,
则PB===.
17.解:(1)证明:∵DP平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴,
∴PA BD=PB AE;
(2)在线段BC上存在一点M,使得四边形ADME是菱形,
证明:过点D作DF⊥PB于点F,作DG⊥AC于点G,连接EF,
∵DP平分∠APB,
AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0,
解得:AE=2,BD=3,
∴由(1)可知:,
∴cos∠APC==,
∴cos∠BDF=cos∠APC=,
∴,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=AE,
∴四边形ADFE是菱形,
此时点F即为M点,
∵cos∠BAC=cos∠APC=,
∴sin∠BAC=,
∴,
∴DG=,
∴在线段BC上存在一点M,使得四边形ADME是菱形,
其面积为:DG AE=2×=.
18.解:(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线;
(2)①∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC
②由△CBH∽△OBC可知:
∵AB=8,
∴BC2=HB OC=4HB,
∴HB=,
∴OH=OB﹣HB=4﹣
∵CB=CH,
∴OH+HC=4+BC,
当∠BOC=90°,
此时BC=4
∵∠BOC<90°,
∴0<BC<4,
令BC=x
∴OH+HC=﹣(x﹣2)2+5
当x=2时,
∴OH+HC可取得最大值,最大值为5
19.(1)证明:如图,连接OD,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
∴OD⊥BC,
∴BC为圆O的切线;
(2)解:连接DF,由(1)知BC为圆O的切线,
∴∠FDC=∠DAF,
∴∠CDA=∠CFD,
∴∠AFD=∠ADB,
∵∠BAD=∠DAF,
∴△ABD∽△ADF,
∴=,即AD2=AB AF=xy,
则AD=;
(3)解:连接EF,在Rt△BOD中,sinB==,
设圆的半径为r,可得=,
解得:r=5,
∴AE=10,AB=18,
∵AE是直径,
∴∠AFE=∠C=90°,
∴EF∥BC,
∴∠AEF=∠B,
∴sin∠AEF==,
∴AF=AE sin∠AEF=10×=,
∵AF∥OD,
∴===,即DG=AD,
∴AD===,
则DG=×=.
