人教版七年级上册数学 第一章有理数 有理数的乘除法则小结复习(共36张)
文档属性
| 名称 | 人教版七年级上册数学 第一章有理数 有理数的乘除法则小结复习(共36张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 19:23:16 | ||
图片预览









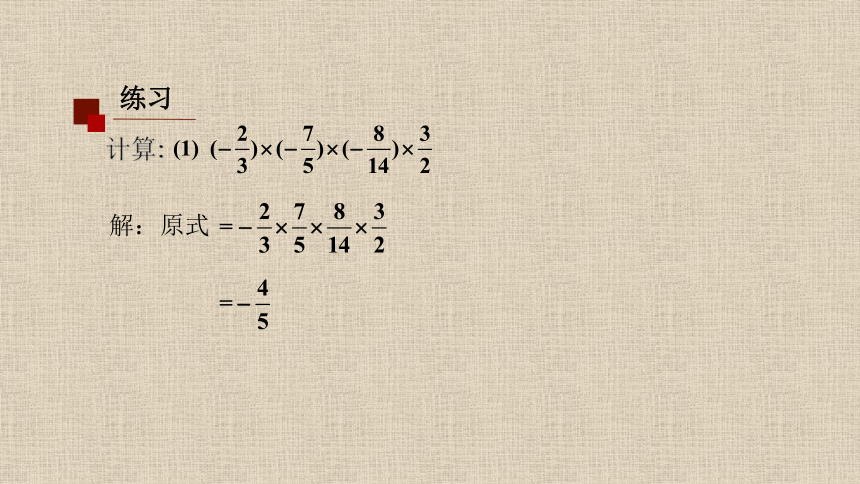
文档简介
(共36张PPT)
有理数的乘除法则小结复习
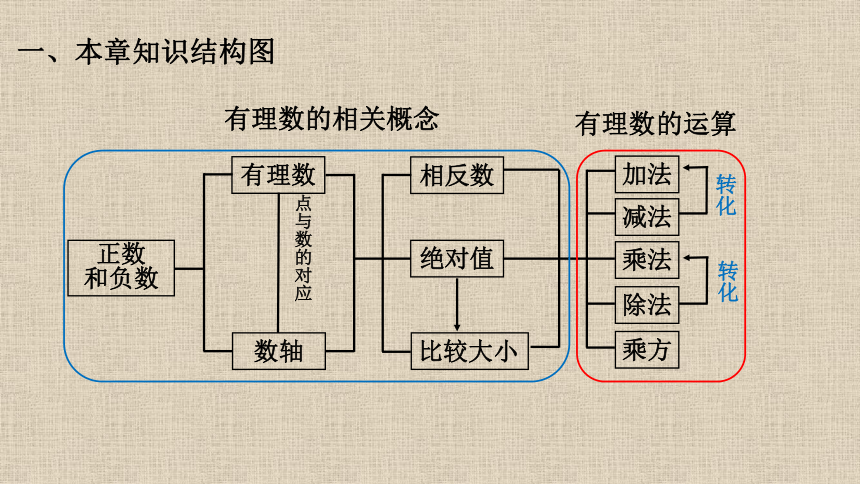
一、本章知识结构图
正数
和负数
有理数
数轴
点与数的对应
相反数
绝对值
比较大小
加法
减法
乘法
除法
乘方
转化
转化
有理数的运算
有理数的相关概念
二、有理数的乘除运算法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数与0相乘,都得0.
乘法法则
我们说
和
互为倒数,
和
互为倒数,
和
互为倒数,
乘积是1的两个数互为倒数.
归纳:正数的倒数是正数,负数的倒数是负数,0没有倒数
思考:数
的倒数是什么?
5×(-6)=(-6)×5
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
乘法交换律: ab=ba 注:a×b可写为a·b或 ab
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
乘法结合律: (ab)c=a(bc)
[3×(-4)]×(-5) = 3×[(-4) ×(-5)]
=60
一般地, 一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律: a(b+c)=ab+ac
5×[3+(-7)] =5×3 +5×(-7)
如: abcd=d(ac)b
如:a(b+c+d)=ab+ac+ad
乘法运算律推广到多个有理数相乘
1.三个以上有理数相乘
2.一个数同几个数的和相乘
几个不是 0 的数相乘,积的符号由负因数的个数决定.
当负因数的个数是偶数时,积为正;
当负因数的个数是奇数时,积为负.
多个有理数相乘的积的符号规律
简记为“奇负偶正”.
1.先观察是否有因数为0;
2.确定积的符号(奇负偶正);
3.确定积的绝对值.
多个有理数乘法运算步骤
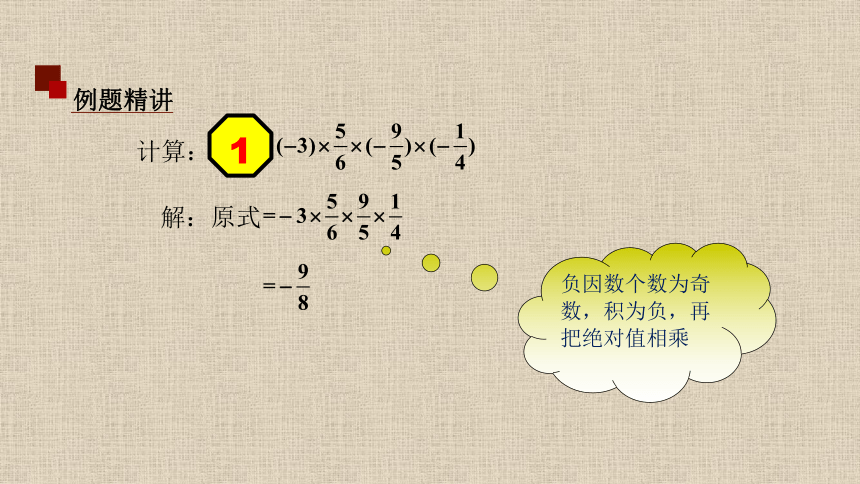
负因数个数为奇数,积为负,再把绝对值相乘
解:原式
例题精讲
计算:
1
练习
计算:
解:原式
负因数个数为偶数,积为正,再把绝对值相乘
解:原式
2
负因数个数为偶数,积为正,再把绝对值相乘
计算:
解:原式
练习
小数化
成分数
(负因数个数为奇数,积为负,再把绝对值相乘)
解:原式
3
带分数化成
假分数
(负因数个数为奇数,积为负,再把绝对值相乘)
解:原式
4
(负因数个数为偶数,积为正,再把绝对值相乘)
小数化成假分数
解:原式
5
计算: (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
解:原式=-8× ×12 × ×0.1
=-1×4×0.1
=-0.4
先观察是否有因数0
(几个数相乘, 如果其中有因数为 0 ,积等于0)
解:原式
6
(乘法结合律)
解:原式
7
= -85×25×4
=-85×(25×4)
(乘法分配律)
解:原式
8
解:原式
ab+ac=a(b+c)
解:原式
9
解:
练习 计算:
(交换律和结合律)
解:原式
10
1
2
3
4
课堂练习
2.两数相除,同号得 ,异号得 ,并把绝对值
相 . 0除以任何一个不等于0的数,都得 .
1.除以一个不等于0的数,等于乘这个数的
正
负
除
0
倒数.
这个法则也可以表示成
除法法则
1.两个法则都可以用来求两个有理数相除.
2.如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
要点归纳:
计算:
提示:在进行有理数除法运算时,能整除的情况下,往往采用法则的后一种形式,在确定符号后,直接除;
解:
典例精析
1
提示:在不能整除或除数为分数的情况下,则往往将除数换成倒数,转化为乘法运算.
解:
2
解:原式
3
解: 原式
这里运用了
分配律
原式
4
典例精析
解:
提示:乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果.
乘除混合运算
1
1
2
3
4
5
6
课堂练习
1.有理数的乘除运算法则和有理数的乘除混合运算.
2.首先要审题,判断能否用运算律进行简便运算,然后确定运算顺序,
最后在每一步的运算过程中,先定符号、再定绝对值.
需要注意的问题:
乘除混合运算不要改变运算顺序,按从左至右的顺序依次进行;
根据算式特征,适当运用运算律使运算更简便.
课堂小结
有理数的乘除法则小结复习
一、本章知识结构图
正数
和负数
有理数
数轴
点与数的对应
相反数
绝对值
比较大小
加法
减法
乘法
除法
乘方
转化
转化
有理数的运算
有理数的相关概念
二、有理数的乘除运算法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数与0相乘,都得0.
乘法法则
我们说
和
互为倒数,
和
互为倒数,
和
互为倒数,
乘积是1的两个数互为倒数.
归纳:正数的倒数是正数,负数的倒数是负数,0没有倒数
思考:数
的倒数是什么?
5×(-6)=(-6)×5
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
乘法交换律: ab=ba 注:a×b可写为a·b或 ab
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
乘法结合律: (ab)c=a(bc)
[3×(-4)]×(-5) = 3×[(-4) ×(-5)]
=60
一般地, 一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律: a(b+c)=ab+ac
5×[3+(-7)] =5×3 +5×(-7)
如: abcd=d(ac)b
如:a(b+c+d)=ab+ac+ad
乘法运算律推广到多个有理数相乘
1.三个以上有理数相乘
2.一个数同几个数的和相乘
几个不是 0 的数相乘,积的符号由负因数的个数决定.
当负因数的个数是偶数时,积为正;
当负因数的个数是奇数时,积为负.
多个有理数相乘的积的符号规律
简记为“奇负偶正”.
1.先观察是否有因数为0;
2.确定积的符号(奇负偶正);
3.确定积的绝对值.
多个有理数乘法运算步骤
负因数个数为奇数,积为负,再把绝对值相乘
解:原式
例题精讲
计算:
1
练习
计算:
解:原式
负因数个数为偶数,积为正,再把绝对值相乘
解:原式
2
负因数个数为偶数,积为正,再把绝对值相乘
计算:
解:原式
练习
小数化
成分数
(负因数个数为奇数,积为负,再把绝对值相乘)
解:原式
3
带分数化成
假分数
(负因数个数为奇数,积为负,再把绝对值相乘)
解:原式
4
(负因数个数为偶数,积为正,再把绝对值相乘)
小数化成假分数
解:原式
5
计算: (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
解:原式=-8× ×12 × ×0.1
=-1×4×0.1
=-0.4
先观察是否有因数0
(几个数相乘, 如果其中有因数为 0 ,积等于0)
解:原式
6
(乘法结合律)
解:原式
7
= -85×25×4
=-85×(25×4)
(乘法分配律)
解:原式
8
解:原式
ab+ac=a(b+c)
解:原式
9
解:
练习 计算:
(交换律和结合律)
解:原式
10
1
2
3
4
课堂练习
2.两数相除,同号得 ,异号得 ,并把绝对值
相 . 0除以任何一个不等于0的数,都得 .
1.除以一个不等于0的数,等于乘这个数的
正
负
除
0
倒数.
这个法则也可以表示成
除法法则
1.两个法则都可以用来求两个有理数相除.
2.如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
要点归纳:
计算:
提示:在进行有理数除法运算时,能整除的情况下,往往采用法则的后一种形式,在确定符号后,直接除;
解:
典例精析
1
提示:在不能整除或除数为分数的情况下,则往往将除数换成倒数,转化为乘法运算.
解:
2
解:原式
3
解: 原式
这里运用了
分配律
原式
4
典例精析
解:
提示:乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果.
乘除混合运算
1
1
2
3
4
5
6
课堂练习
1.有理数的乘除运算法则和有理数的乘除混合运算.
2.首先要审题,判断能否用运算律进行简便运算,然后确定运算顺序,
最后在每一步的运算过程中,先定符号、再定绝对值.
需要注意的问题:
乘除混合运算不要改变运算顺序,按从左至右的顺序依次进行;
根据算式特征,适当运用运算律使运算更简便.
课堂小结
