华东师大版数学八年级上册 第14章 勾股定理 复习(课件)(共19张ppt)
文档属性
| 名称 | 华东师大版数学八年级上册 第14章 勾股定理 复习(课件)(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 262.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 19:21:15 | ||
图片预览






文档简介
(共19张PPT)
第14章 勾股定理 复习课件
1.了解勾股定理的内容和名字的由来, 并会用它来解决一些有关直角三角形的计算问题。
2.理解勾股定理常见的证明方法,并会 用这种思想来求一些图形面积问题。
3.会用勾股定理判断是否是一组勾股数。
知识点目标
4.理解勾股定理逆定理的含义,并会用它来判断一个三角形是否是直角三角形。
5.能区分和辨认勾股定理与勾股定理逆定理,并会简单的综合运用。
6.能用勾股定理解决生活中的实际问题。
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方。
勾股逆定理
如果三角形的三边长a,b,c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
满足a2 +b2=c2的三个正整数,称为勾股数。
勾 股 数
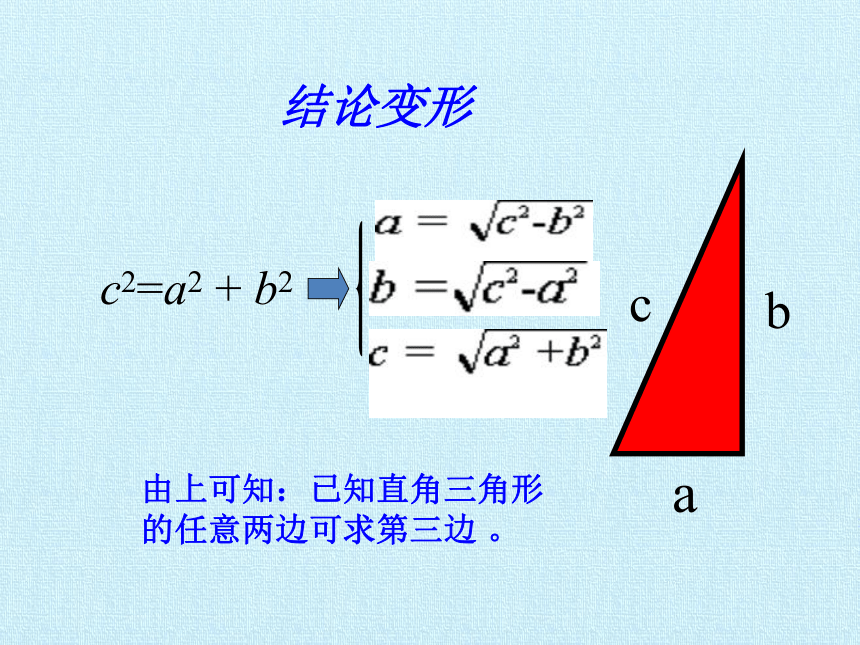
结论变形
a
b
c
c2=a2 + b2
由上可知:已知直角三角形
的任意两边可求第三边 。
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。
2.直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。
13
20
11
24
60/13
填空题
3 .如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、 B、 C、 D的面积和是______。
49cm2
4.已知:如图,△ABC中,∠C = 90°,点O为
△ABC的三条角平分线的交点,OF⊥BC,OE
⊥AC,OD⊥AB,点D、E、F分别是垂足,且
BC = 8cm,CA = 6cm,则点O到三边AB,AC和
BC的距离分别等于 cm。
F
B
C
A
D
E
O
2,
2,
2
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6, b=8, c=10 D、a=3,b=4,c=5
D
A
3.直角三角形一直角边的长为11,另两边为自然数,则直角三角形的周长为( )
A、121 B、120 C、132 D、不能确定
C
选择题
4.如果直角三角形的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
5.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
6.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
D
A
B
1.如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
C
A
E
B
D
解答题
解:
设AE= xkm,则 BE=(25-x)km
根据勾股定理,得:
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x
25-x
C
A
E
B
D
15
10
2.已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
提示:先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了。
解答题
3.已知,如图,在Rt△ABC中,∠C=90°,
将△ACD沿AD折叠,使得C点与E点重合 ,CD=1.5, BD=2.5,求AC的长。
D
A
C
B
E
解答题
如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC。
A
B
P
C
思考题
解:
过A点做AD⊥BC
A
B
P
C
D
在 Rt△ABD中,根据勾股定理,得:
AB2=AD2+BD2 ①
同理: AP2=AD2+DP2 ②
由①-②,得
AB2-AP2=BD2-DP2
=(BD+DP)(BD-DP)
=PB(BD+DP)
又 AB=AC, AD⊥BC ∴ BD=CD
∴ AB2-AP2=PB×PC
如图,在△ABC中,AB=AC,P为BC上任意一点,试说明:AB2-AP2=PB×PC。
三、小结
本节课主要是应用勾股定理和它的逆定理来解决问题,在应用定理时,应注意:1.没有图的要按题意画好图并标上字母;2.不要用错定理。
谢 谢
第14章 勾股定理 复习课件
1.了解勾股定理的内容和名字的由来, 并会用它来解决一些有关直角三角形的计算问题。
2.理解勾股定理常见的证明方法,并会 用这种思想来求一些图形面积问题。
3.会用勾股定理判断是否是一组勾股数。
知识点目标
4.理解勾股定理逆定理的含义,并会用它来判断一个三角形是否是直角三角形。
5.能区分和辨认勾股定理与勾股定理逆定理,并会简单的综合运用。
6.能用勾股定理解决生活中的实际问题。
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方。
勾股逆定理
如果三角形的三边长a,b,c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
满足a2 +b2=c2的三个正整数,称为勾股数。
勾 股 数
结论变形
a
b
c
c2=a2 + b2
由上可知:已知直角三角形
的任意两边可求第三边 。
1.在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。
2.直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。
13
20
11
24
60/13
填空题
3 .如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、 B、 C、 D的面积和是______。
49cm2
4.已知:如图,△ABC中,∠C = 90°,点O为
△ABC的三条角平分线的交点,OF⊥BC,OE
⊥AC,OD⊥AB,点D、E、F分别是垂足,且
BC = 8cm,CA = 6cm,则点O到三边AB,AC和
BC的距离分别等于 cm。
F
B
C
A
D
E
O
2,
2,
2
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
2.下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6, b=8, c=10 D、a=3,b=4,c=5
D
A
3.直角三角形一直角边的长为11,另两边为自然数,则直角三角形的周长为( )
A、121 B、120 C、132 D、不能确定
C
选择题
4.如果直角三角形的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
5.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
6.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
D
A
B
1.如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
C
A
E
B
D
解答题
解:
设AE= xkm,则 BE=(25-x)km
根据勾股定理,得:
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x
25-x
C
A
E
B
D
15
10
2.已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
提示:先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了。
解答题
3.已知,如图,在Rt△ABC中,∠C=90°,
将△ACD沿AD折叠,使得C点与E点重合 ,CD=1.5, BD=2.5,求AC的长。
D
A
C
B
E
解答题
如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC。
A
B
P
C
思考题
解:
过A点做AD⊥BC
A
B
P
C
D
在 Rt△ABD中,根据勾股定理,得:
AB2=AD2+BD2 ①
同理: AP2=AD2+DP2 ②
由①-②,得
AB2-AP2=BD2-DP2
=(BD+DP)(BD-DP)
=PB(BD+DP)
又 AB=AC, AD⊥BC ∴ BD=CD
∴ AB2-AP2=PB×PC
如图,在△ABC中,AB=AC,P为BC上任意一点,试说明:AB2-AP2=PB×PC。
三、小结
本节课主要是应用勾股定理和它的逆定理来解决问题,在应用定理时,应注意:1.没有图的要按题意画好图并标上字母;2.不要用错定理。
谢 谢
