2021-2022学年苏科版九年级数学下册7.2正弦、余弦 课后综合练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册7.2正弦、余弦 课后综合练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览



文档简介
7.2正弦、余弦---课后综合练---2021-2022学年九年级数学下册(苏科版)
一、选择题
1、已知在中,,则下列式子中正确的是( )
A. B. C. D.
2、在中,,,,则等于( )
A.3 B.2 C. D.
3、在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
4、在中,,、、的对边分别是、、,下列结论正确的是
A. B. C. D.
5、如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,
则图中∠ABC的余弦值是( )
A.2 B. C. D.
6、如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
7、如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cos a=,AB=4,
则AD的长为 ( )
A.3 B. C. D.
8、如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B=,E为边AC的中点,则 cos∠ADE的值为( )
A. B. C. D.
9、如图,在中,,于,若,,则的长为
A. B.10 C. D.12
10、如图,在中,于点,若,则的值为( )
A. B. C. D.
二、填空题
11、在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
12、若a是锐角,且sin2 a+cos2 48°=1,则a= .
13、如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子AB的长度为 米.
14、如图,在中,,点为边的中点,连接,若,,则的值为______.
15、如图.在的正方形方格图形中,小正方形的顶点称为格点.的顶点都在格点上,
则的正弦值是__________.
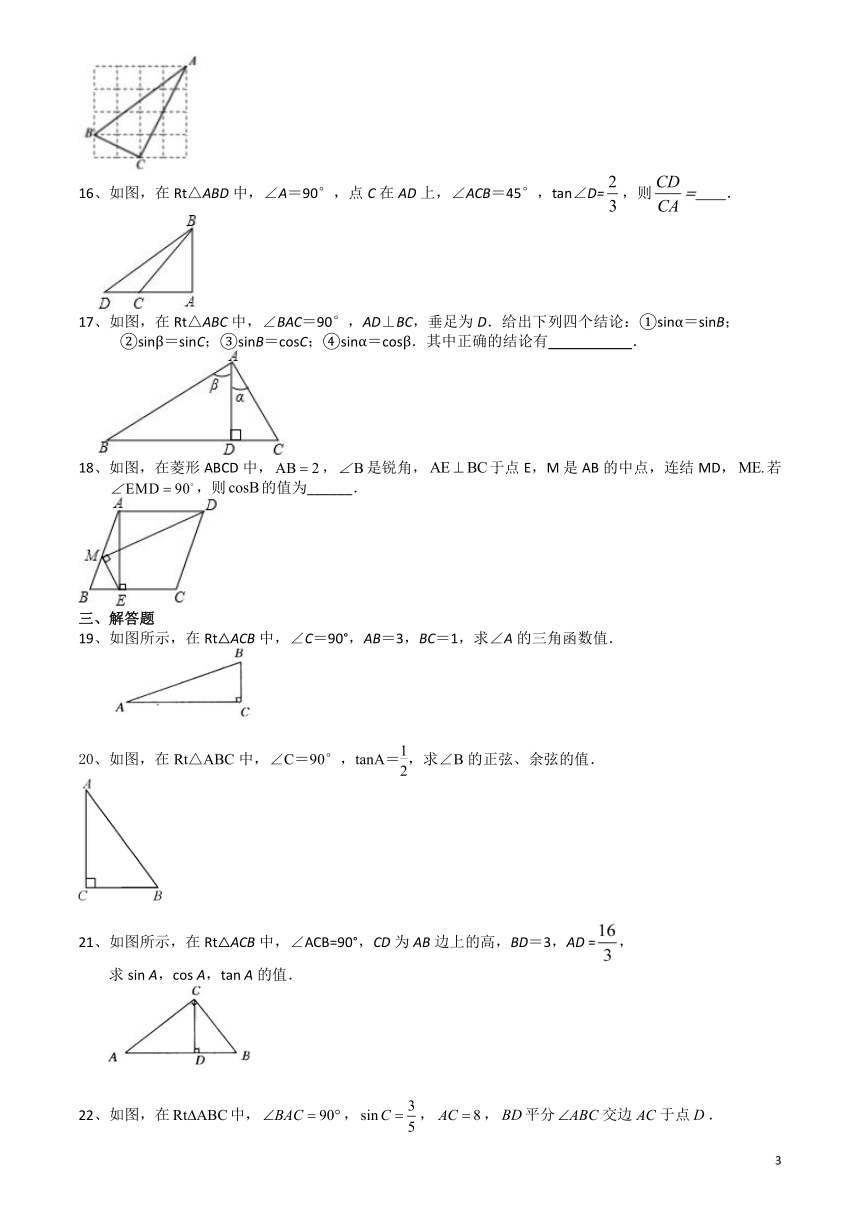
16、如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则= .
17、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;
②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有 .
18、如图,在菱形ABCD中,,是锐角,于点E,M是AB的中点,连结MD,若,则的值为______.
三、解答题
19、如图所示,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值.
20、如图,在Rt△ABC中,∠C=90°,tanA=,求∠B的正弦、余弦的值.
21、如图所示,在Rt△ACB中,∠ACB=90°,CD为AB边上的高,BD=3,AD =,
求sin A,cos A,tan A的值.
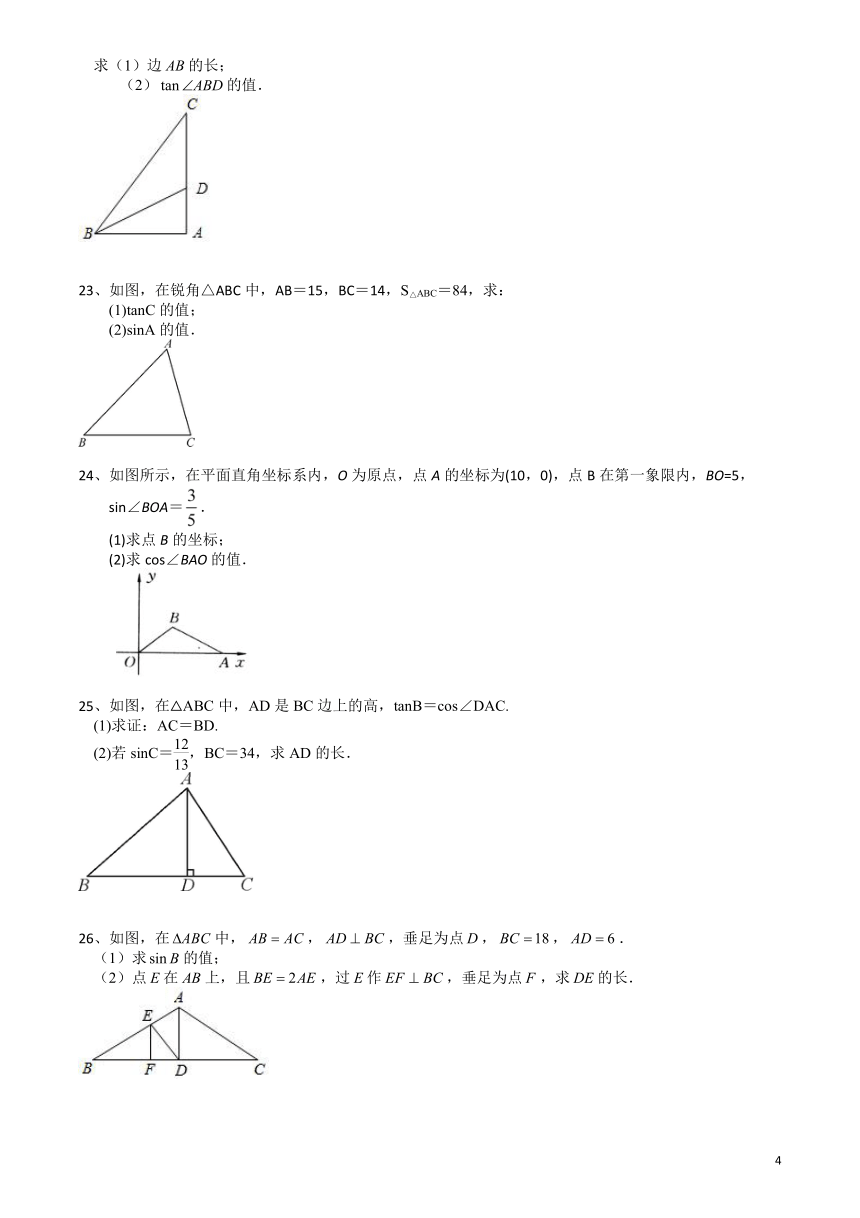
22、如图,在中,,,,平分交边于点.
求(1)边的长;
(2)的值.
23、如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
24、如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,
sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
25、如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD.
(2)若sinC=,BC=34,求AD的长.
26、如图,在中,,,垂足为点,,.
(1)求的值;
(2)点在上,且,过作,垂足为点,求的长.
7.2正弦、余弦---课后综合练---2021-2022学年九年级数学下册(苏科版)(解析)
一、选择题
1、已知在中,,则下列式子中正确的是( )
A. B. C. D.
【答案】A
【分析】
由勾股定理求出,然后根据锐角三角函数定义判断即可.
【详解】
解:在中,,
,
,,,
故选:A.
2、在中,,,,则等于( )
A.3 B.2 C. D.
【答案】B
【分析】直接根据余弦定义求解即可.
【详解】解:∵中,,,,
∴,
∴AC==2.
故选B.
3、在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
【答案】A
【分析】根据正切的定义和勾股定理可得AB的长,根据正弦的定义可得答案.
【详解】解:∵ ,
∴在中,设BC=x,AC=3x,
由勾股定理得:
∴AB==x,
∴sinA===,
故选:A.
4、在中,,、、的对边分别是、、,下列结论正确的是
A. B. C. D.
【分析】根据三角函数定义:(1)正弦:我们把锐角的对边与斜边的比叫做的正弦,记作.
(2)余弦:锐角的邻边与斜边的比叫做的余弦,记作.
(3)正切:锐角的对边与邻边的比叫做的正切,记作.分别进行分析即可.
【解析】在直角中,,则
,则,故选项错误、选项错误;
,则,故选项错误;
,则,故选项正确;
故选:.
5、如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,
则图中∠ABC的余弦值是( )
A.2 B. C. D.
解:∵由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC==.
故选D.
6、如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
解:∵D(0,3),C(4,0),
∴OD=3,OC=4,
∵∠COD=90°,
∴CD==5,
连接CD,如图所示:
∵∠OBD=∠OCD,
∴sin∠OBD=sin∠OCD==.
故选:D.
7、如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cos a=,AB=4,
则AD的长为 ( )
A.3 B. C. D.
解:∠ADE和∠EDC互余,∴cos a=sin∠EDC=,sin∠EDC=
∴EC=.
由勾股定理,得DE=.在Rt△AED中,cos a=,∴AD=.故选B.
8、如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B=,E为边AC的中点,则 cos∠ADE的值为( )
A. B. C. D.
【答案】D
【分析】根据直角三角形勾股定理及余弦函数可得,再由勾股定理可得,根据直角三角形中斜边上中线等于斜边的一半可得,依据等边对等角可得,由此计算角的余弦即可.
【详解】解:∵于D,,,
∴,,
∵,∴,
∵E为AC中点,∴,∴,
∴,
故选:D.
9、如图,在中,,于,若,,则的长为
A. B.10 C. D.12
【答案】B
【分析】
先证得再解直角三角形ACD得、代入计算可得.
【详解】
解:,,,
,,
,,,
在中,,,
,则,
由得,
故选:B.
10、如图,在中,于点,若,则的值为( )
A. B. C. D.
【答案】B
【分析】
先根据题目已知条件推出∽,则可得,然后根据,设,,利用对应边成比例表示出的值,进而得出的值,
【详解】
∵在中,,∴,
∵于点,∴,
∴,,
∴∽,∴,即,,
∵,∴设,,
∴,∴,
故选:B.
二、填空题
11、在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
【解答】解:如图所示:∵∠C=90°,AC=5,BC=12,
∴AB==13,
∴sinA=.
故答案为:.
12、若a是锐角,且sin2 a+cos2 48°=1,则a= .
解:∵sin2 a+cos2 a=l,∴a=48°.
13、如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子AB的长度为 米.
解:在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米.
14、如图,在中,,点为边的中点,连接,若,,则的值为______.
【答案】
【分析】根据直角三角形斜边上的中线是斜边的一半得到DC=DB,∠DCB=∠B,根据锐角三角函数的定义即可求解.
【详解】∵∠ACB=90°,BC=4,CD=3,点D是AB边的中点,
∴DC=DB,
∴∠DCB=∠B,AB=2CD=6,
∴,
故答案为:.
15、如图.在的正方形方格图形中,小正方形的顶点称为格点.的顶点都在格点上,
则的正弦值是__________.
【答案】
【详解】分析:先根据勾股定理的逆定理判断出△ABC的形状,再由锐角三角函数的定义即可得出结论.
详解:∵AB2=32+42=25,AC2=22+42=20,BC2=12+22=5,∴AC2+BC2=AB2,∴△ABC为直角三角形,且∠ACB=90°,则sin∠BAC==.
故答案为.
16、如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则= .
【分析】由tan∠D=可设AB=2x、AD=3x,根据∠ACB=45°知AC=AB=2x,得出CD=x,继而可得答案.
【解析】在Rt△ABD中,∵tan∠D=,
∴设AB=2x,AD=3x,
∵∠ACB=45°,
∴AC=AB=2x,
则CD=AD﹣AC=3x﹣2x=x,
∴,
故答案为:.
17、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;
②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有 .
【分析】本题主要考查锐角三角函数的定义,根据∠A=90°,AD⊥BC,可得∠α=∠B,∠β=∠C,再利用锐角三角函数的定义可列式进行逐项判断.
【解析】∵∠BAC=90°,AD⊥BC,∴∠α+∠β=90°,∠B+∠β=90°,∠B+∠C=90°,
∴∠α=∠B,∠β=∠C,∴sinα=sinB,故①正确; sinβ=sinC,故②正确;
∵在Rt△ABC中sinB=,cosC=,∴sinB=cosC,故③正确;
∵sinα=sinB,cos∠β=cosC, ∴sinα=cos∠β,故④正确;
故答案为①②③④.
18、如图,在菱形ABCD中,,是锐角,于点E,M是AB的中点,连结MD,若,则的值为______.
【答案】
【详解】【分析】延长DM交CB的延长线于点首先证明,设,利用勾股定理构建方程求出x即可解决问题.
【详解】延长DM交CB的延长线于点H,
四边形ABCD是菱形,,,,
,,≌,,
,,设,
,,,
,
,或舍弃,
,
故答案为.
三、解答题
19、如图所示,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值.
解:AC=
sin A==,cos A==,tan A==.
20、如图,在Rt△ABC中,∠C=90°,tanA=,求∠B的正弦、余弦的值.
解:∵∠C=90°,tanA=,∴设BC=x,AC=2x,∴AB=x,
∴sinB===, cosB===
21、如图所示,在Rt△ACB中,∠ACB=90°,CD为AB边上的高,BD=3,AD =,
求sin A,cos A,tan A的值.
解:∵∠ACB=90°,CD⊥AB,∴△ACD∽△CBD,∴CD2=AD·DB=16,∴CD=4,
∴AC=.∴sin A==,cos A =,tan A=.
22、如图,在中,,,,平分交边于点.
求(1)边的长;
(2)的值.
【分析】(1)在中,由推出,即可解决问题;
(2)过点作于点.由角平分线的性质定理可知,设,在中,利用勾股定理构建方程求出即可解决问题;
【解析】(1)在中,,
又, .
(2)过点作于点.
平分,,,,
设,
在中,,.,
,,,
在中,可得.
23、如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
解:(1)过A作AD⊥BC于点D.
∵S△ABC=BC·AD=84,∴×14×AD=84,∴AD=12,
又∵AB=15,
∴在Rt△ABD中,BD==9,
∴CD=14-9=5.
在Rt△ADC中,AC==13,
∴tanC==
(2)过B作BE⊥AC于点E,
∵S△ABC=AC·BE=84,∴BE=,
∴sin∠BAC===
24、如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,
sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
解:(1)如图所示,作BH⊥OA, 垂足为H.
在Rt△OHB中,∵BO=5,sin∠BOA=,∴BH=3,
∴OH=4,∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,∴AB=,
∴cos∠BAO== .
25、如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD.
(2)若sinC=,BC=34,求AD的长.
(1)证明:∵tanB=cos∠DAC,
∴=,∴AC=BD.
(2)设AC=BD=x(x>0),
则CD=BC-BD=34-x.
∵sinC==,∴cosC=,∴=,
即=,
解得x=,即AC=.
∴AD=AC·sinC=×=.
26、如图,在中,,,垂足为点,,.
(1)求的值;
(2)点在上,且,过作,垂足为点,求的长.
【分析】(1)先利用等腰三角形三线合一的性质求出,然后在中,利用勾股定理求出,再根据计算即可;
(2)由,,可得,求出、,再利用勾股定理解决问题.
【解析】(1),,,,
,
;
(2),,,,
,,
,
在中,.
一、选择题
1、已知在中,,则下列式子中正确的是( )
A. B. C. D.
2、在中,,,,则等于( )
A.3 B.2 C. D.
3、在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
4、在中,,、、的对边分别是、、,下列结论正确的是
A. B. C. D.
5、如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,
则图中∠ABC的余弦值是( )
A.2 B. C. D.
6、如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
7、如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cos a=,AB=4,
则AD的长为 ( )
A.3 B. C. D.
8、如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B=,E为边AC的中点,则 cos∠ADE的值为( )
A. B. C. D.
9、如图,在中,,于,若,,则的长为
A. B.10 C. D.12
10、如图,在中,于点,若,则的值为( )
A. B. C. D.
二、填空题
11、在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
12、若a是锐角,且sin2 a+cos2 48°=1,则a= .
13、如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子AB的长度为 米.
14、如图,在中,,点为边的中点,连接,若,,则的值为______.
15、如图.在的正方形方格图形中,小正方形的顶点称为格点.的顶点都在格点上,
则的正弦值是__________.
16、如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则= .
17、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;
②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有 .
18、如图,在菱形ABCD中,,是锐角,于点E,M是AB的中点,连结MD,若,则的值为______.
三、解答题
19、如图所示,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值.
20、如图,在Rt△ABC中,∠C=90°,tanA=,求∠B的正弦、余弦的值.
21、如图所示,在Rt△ACB中,∠ACB=90°,CD为AB边上的高,BD=3,AD =,
求sin A,cos A,tan A的值.
22、如图,在中,,,,平分交边于点.
求(1)边的长;
(2)的值.
23、如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
24、如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,
sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
25、如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD.
(2)若sinC=,BC=34,求AD的长.
26、如图,在中,,,垂足为点,,.
(1)求的值;
(2)点在上,且,过作,垂足为点,求的长.
7.2正弦、余弦---课后综合练---2021-2022学年九年级数学下册(苏科版)(解析)
一、选择题
1、已知在中,,则下列式子中正确的是( )
A. B. C. D.
【答案】A
【分析】
由勾股定理求出,然后根据锐角三角函数定义判断即可.
【详解】
解:在中,,
,
,,,
故选:A.
2、在中,,,,则等于( )
A.3 B.2 C. D.
【答案】B
【分析】直接根据余弦定义求解即可.
【详解】解:∵中,,,,
∴,
∴AC==2.
故选B.
3、在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
【答案】A
【分析】根据正切的定义和勾股定理可得AB的长,根据正弦的定义可得答案.
【详解】解:∵ ,
∴在中,设BC=x,AC=3x,
由勾股定理得:
∴AB==x,
∴sinA===,
故选:A.
4、在中,,、、的对边分别是、、,下列结论正确的是
A. B. C. D.
【分析】根据三角函数定义:(1)正弦:我们把锐角的对边与斜边的比叫做的正弦,记作.
(2)余弦:锐角的邻边与斜边的比叫做的余弦,记作.
(3)正切:锐角的对边与邻边的比叫做的正切,记作.分别进行分析即可.
【解析】在直角中,,则
,则,故选项错误、选项错误;
,则,故选项错误;
,则,故选项正确;
故选:.
5、如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,
则图中∠ABC的余弦值是( )
A.2 B. C. D.
解:∵由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC==.
故选D.
6、如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
解:∵D(0,3),C(4,0),
∴OD=3,OC=4,
∵∠COD=90°,
∴CD==5,
连接CD,如图所示:
∵∠OBD=∠OCD,
∴sin∠OBD=sin∠OCD==.
故选:D.
7、如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=a,且cos a=,AB=4,
则AD的长为 ( )
A.3 B. C. D.
解:∠ADE和∠EDC互余,∴cos a=sin∠EDC=,sin∠EDC=
∴EC=.
由勾股定理,得DE=.在Rt△AED中,cos a=,∴AD=.故选B.
8、如图,在△ABC中,AD⊥BC于点D.若BD=9,DC=5,cos B=,E为边AC的中点,则 cos∠ADE的值为( )
A. B. C. D.
【答案】D
【分析】根据直角三角形勾股定理及余弦函数可得,再由勾股定理可得,根据直角三角形中斜边上中线等于斜边的一半可得,依据等边对等角可得,由此计算角的余弦即可.
【详解】解:∵于D,,,
∴,,
∵,∴,
∵E为AC中点,∴,∴,
∴,
故选:D.
9、如图,在中,,于,若,,则的长为
A. B.10 C. D.12
【答案】B
【分析】
先证得再解直角三角形ACD得、代入计算可得.
【详解】
解:,,,
,,
,,,
在中,,,
,则,
由得,
故选:B.
10、如图,在中,于点,若,则的值为( )
A. B. C. D.
【答案】B
【分析】
先根据题目已知条件推出∽,则可得,然后根据,设,,利用对应边成比例表示出的值,进而得出的值,
【详解】
∵在中,,∴,
∵于点,∴,
∴,,
∴∽,∴,即,,
∵,∴设,,
∴,∴,
故选:B.
二、填空题
11、在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
【解答】解:如图所示:∵∠C=90°,AC=5,BC=12,
∴AB==13,
∴sinA=.
故答案为:.
12、若a是锐角,且sin2 a+cos2 48°=1,则a= .
解:∵sin2 a+cos2 a=l,∴a=48°.
13、如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子AB的长度为 米.
解:在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米.
14、如图,在中,,点为边的中点,连接,若,,则的值为______.
【答案】
【分析】根据直角三角形斜边上的中线是斜边的一半得到DC=DB,∠DCB=∠B,根据锐角三角函数的定义即可求解.
【详解】∵∠ACB=90°,BC=4,CD=3,点D是AB边的中点,
∴DC=DB,
∴∠DCB=∠B,AB=2CD=6,
∴,
故答案为:.
15、如图.在的正方形方格图形中,小正方形的顶点称为格点.的顶点都在格点上,
则的正弦值是__________.
【答案】
【详解】分析:先根据勾股定理的逆定理判断出△ABC的形状,再由锐角三角函数的定义即可得出结论.
详解:∵AB2=32+42=25,AC2=22+42=20,BC2=12+22=5,∴AC2+BC2=AB2,∴△ABC为直角三角形,且∠ACB=90°,则sin∠BAC==.
故答案为.
16、如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则= .
【分析】由tan∠D=可设AB=2x、AD=3x,根据∠ACB=45°知AC=AB=2x,得出CD=x,继而可得答案.
【解析】在Rt△ABD中,∵tan∠D=,
∴设AB=2x,AD=3x,
∵∠ACB=45°,
∴AC=AB=2x,
则CD=AD﹣AC=3x﹣2x=x,
∴,
故答案为:.
17、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;
②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有 .
【分析】本题主要考查锐角三角函数的定义,根据∠A=90°,AD⊥BC,可得∠α=∠B,∠β=∠C,再利用锐角三角函数的定义可列式进行逐项判断.
【解析】∵∠BAC=90°,AD⊥BC,∴∠α+∠β=90°,∠B+∠β=90°,∠B+∠C=90°,
∴∠α=∠B,∠β=∠C,∴sinα=sinB,故①正确; sinβ=sinC,故②正确;
∵在Rt△ABC中sinB=,cosC=,∴sinB=cosC,故③正确;
∵sinα=sinB,cos∠β=cosC, ∴sinα=cos∠β,故④正确;
故答案为①②③④.
18、如图,在菱形ABCD中,,是锐角,于点E,M是AB的中点,连结MD,若,则的值为______.
【答案】
【详解】【分析】延长DM交CB的延长线于点首先证明,设,利用勾股定理构建方程求出x即可解决问题.
【详解】延长DM交CB的延长线于点H,
四边形ABCD是菱形,,,,
,,≌,,
,,设,
,,,
,
,或舍弃,
,
故答案为.
三、解答题
19、如图所示,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值.
解:AC=
sin A==,cos A==,tan A==.
20、如图,在Rt△ABC中,∠C=90°,tanA=,求∠B的正弦、余弦的值.
解:∵∠C=90°,tanA=,∴设BC=x,AC=2x,∴AB=x,
∴sinB===, cosB===
21、如图所示,在Rt△ACB中,∠ACB=90°,CD为AB边上的高,BD=3,AD =,
求sin A,cos A,tan A的值.
解:∵∠ACB=90°,CD⊥AB,∴△ACD∽△CBD,∴CD2=AD·DB=16,∴CD=4,
∴AC=.∴sin A==,cos A =,tan A=.
22、如图,在中,,,,平分交边于点.
求(1)边的长;
(2)的值.
【分析】(1)在中,由推出,即可解决问题;
(2)过点作于点.由角平分线的性质定理可知,设,在中,利用勾股定理构建方程求出即可解决问题;
【解析】(1)在中,,
又, .
(2)过点作于点.
平分,,,,
设,
在中,,.,
,,,
在中,可得.
23、如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
解:(1)过A作AD⊥BC于点D.
∵S△ABC=BC·AD=84,∴×14×AD=84,∴AD=12,
又∵AB=15,
∴在Rt△ABD中,BD==9,
∴CD=14-9=5.
在Rt△ADC中,AC==13,
∴tanC==
(2)过B作BE⊥AC于点E,
∵S△ABC=AC·BE=84,∴BE=,
∴sin∠BAC===
24、如图所示,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,
sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
解:(1)如图所示,作BH⊥OA, 垂足为H.
在Rt△OHB中,∵BO=5,sin∠BOA=,∴BH=3,
∴OH=4,∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,∴AB=,
∴cos∠BAO== .
25、如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD.
(2)若sinC=,BC=34,求AD的长.
(1)证明:∵tanB=cos∠DAC,
∴=,∴AC=BD.
(2)设AC=BD=x(x>0),
则CD=BC-BD=34-x.
∵sinC==,∴cosC=,∴=,
即=,
解得x=,即AC=.
∴AD=AC·sinC=×=.
26、如图,在中,,,垂足为点,,.
(1)求的值;
(2)点在上,且,过作,垂足为点,求的长.
【分析】(1)先利用等腰三角形三线合一的性质求出,然后在中,利用勾股定理求出,再根据计算即可;
(2)由,,可得,求出、,再利用勾股定理解决问题.
【解析】(1),,,,
,
;
(2),,,,
,,
,
在中,.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
