2021-2022学年北师大版八年级数学上册第3章位置与坐标 期末复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第3章位置与坐标 期末复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 323.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 15:38:59 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学上册《第3章位置与坐标》期末复习训练(附答案)
1.点M(2,3)关于x轴对称点的坐标为( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(3,﹣2)
2.以下点在第二象限的是( )
A.(0,0) B.(3,﹣5) C.(﹣1,9) D.(﹣2,﹣1)
3.如图,在平面直角坐标系中,△ABC关于直线m(直线m上各点的横坐标都为1)对称,点C的坐标为(4,1),则点B的坐标为( )
A.(﹣2,1) B.(﹣3,1) C.(﹣2,﹣1) D.(2,1)
4.在教室里,如果用(3,2)表示3排2列,那么5排6列可以表示为( )
A.(5,11) B.(11,6) C.(5,6) D.(6,5)
5.已知点P(﹣4,5),Q(﹣2,5),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于x轴 D.以上都不正确
6.已知点C(﹣1,﹣2),D(﹣1,2),则线段CD的长是( )
A.1 B.2 C.3 D.4
7.若点A(﹣3,2)关于y轴对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )
A.(3,2) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
8.若点B(m+1,3m﹣5)到x轴的距离与到y轴的距离相等,则点B的坐标是( )
A.(4,4)或(2,2) B.(4,4)或(2,﹣2)
C.(2,﹣2) D.(4,4)
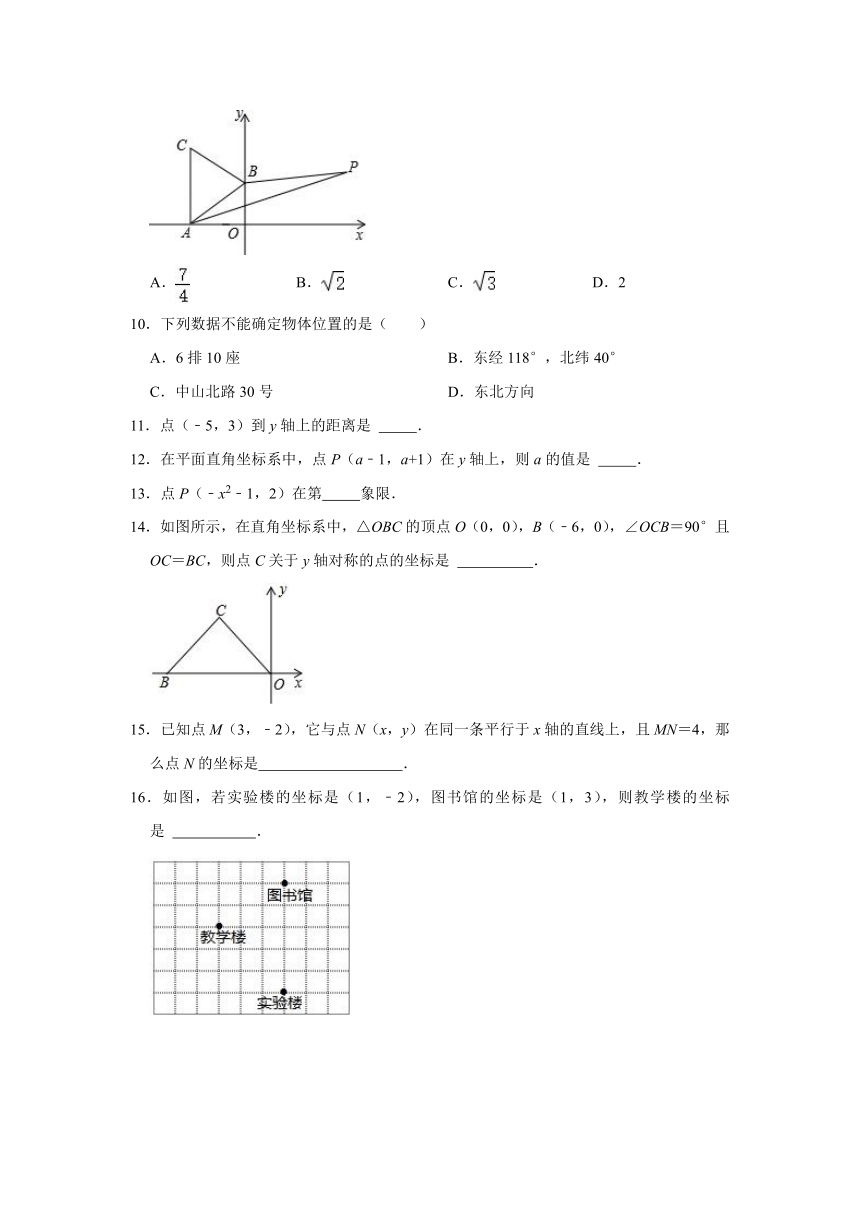
9.如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且在直线AB的下方,满足2S△ABP=S△ABC,则a的值为( )
A. B. C. D.2
10.下列数据不能确定物体位置的是( )
A.6排10座 B.东经118°,北纬40°
C.中山北路30号 D.东北方向
11.点(﹣5,3)到y轴上的距离是 .
12.在平面直角坐标系中,点P(a﹣1,a+1)在y轴上,则a的值是 .
13.点P(﹣x2﹣1,2)在第 象限.
14.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),∠OCB=90°且OC=BC,则点C关于y轴对称的点的坐标是 .
15.已知点M(3,﹣2),它与点N(x,y)在同一条平行于x轴的直线上,且MN=4,那么点N的坐标是 .
16.如图,若实验楼的坐标是(1,﹣2),图书馆的坐标是(1,3),则教学楼的坐标是 .
17.如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若点D与点C关于原点对称,则点D的坐标为 ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
18.如图所示,在长方形ABCD中,已知AB=6,AD=4,在长方形ABCD外画△ABE,使AE=BE=5,请建立适当的平面直角坐标系,并求出各顶点的坐标.
19.已知:如图,写出坐标平面内各点的坐标.
A( , );B( , );
C( , );D( , );
E( , );F( , ).
20.建立平面直角坐标系,使点C的坐标为(4,0),写出点A、B、D、E、F、G的坐标.
21.在平面直角坐标系中,分别根据下列条件,求出各点的坐标.
(1)点A在y轴上,位于原点上方,距离原点2个单位长度;
(2)点B在x轴上,位于原点右侧,距离原点1个单位长度;
(3)点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
(4)点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;
(5)点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.
22.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
23.如图,在直角坐标平面内,已知点A的坐标(﹣4,0),点A关于y轴对称的点为点C.
(1)请在网格图中标出点A和点C.
(2)△ABC的面积是 ;
(3)在y轴上找一点D,使S△ACD=S△ABC,请直接写出点D的坐标 .
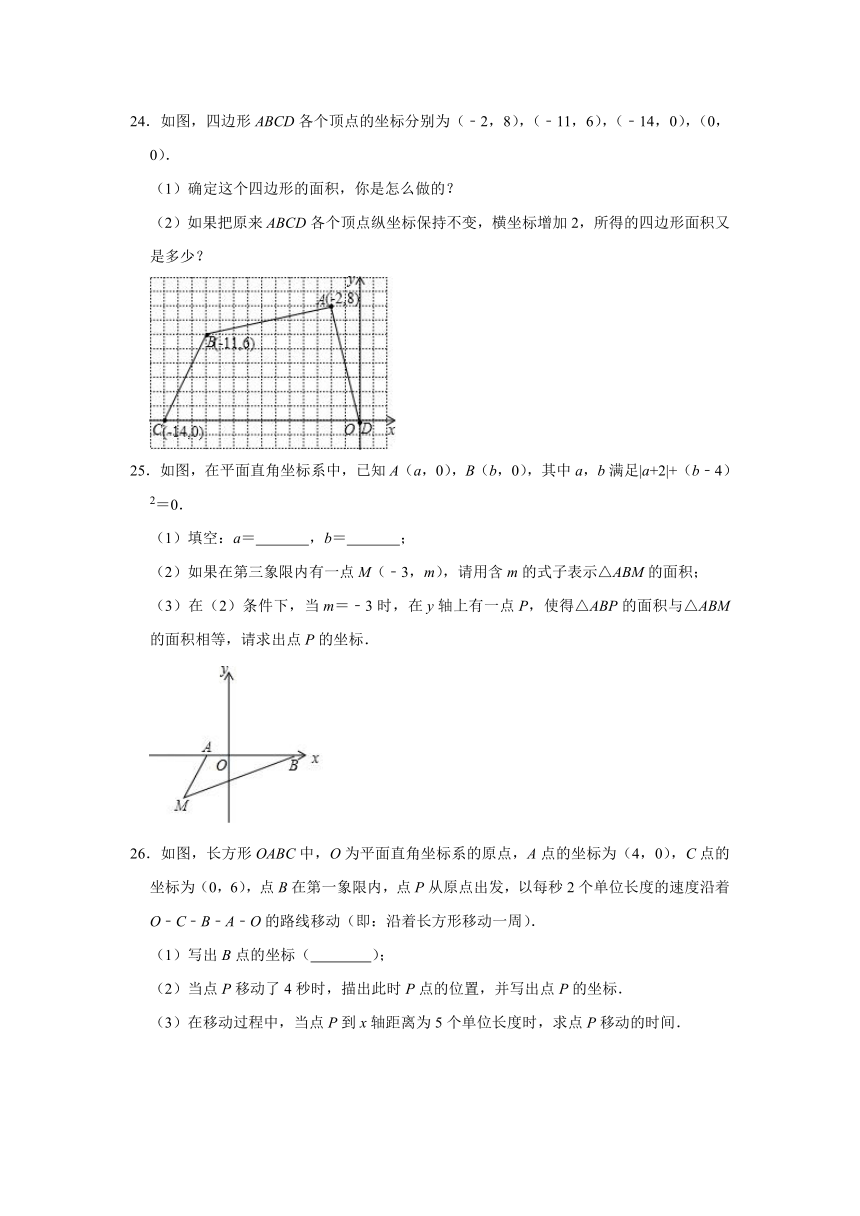
24.如图,四边形ABCD各个顶点的坐标分别为(﹣2,8),(﹣11,6),(﹣14,0),(0,0).
(1)确定这个四边形的面积,你是怎么做的?
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
25.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
26.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)写出B点的坐标( );
(2)当点P移动了4秒时,描出此时P点的位置,并写出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
27.如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
28.如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)(b,c)(如图所示),其中a,b,c满足关系式(a﹣2)2+=0,|c﹣4|≤0.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,1),请用含m的代数式表示△AOP的面积;
(3)在(2)的条件下,是否存在点P,使△AOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.解:点M(2,3)关于x轴对称点的坐标为(2,﹣3),
故选:C.
2.解:A.(0,0)在原点,故本选项不合题意;
B.(3,﹣5)在第四象限,故本选项不合题意;
C.(﹣1,9)在第二象限,故本选项符合题意;
D.(﹣2,﹣1)在第三象限,故本选项不合题意;
故选:C.
3.解:∵△ABC关于直线m(直线m上各点的横坐标都为1)对称,
∴C,B关于直线m对称,即关于直线x=1对称,
∵点C的坐标为(4,1),
∴=1,
解得:x=﹣2,
则点B的坐标为:(﹣2,1).
故选:A.
4.解:用(3,2)表示3排2列,
那么5排6列应先表示排,再表示列,即(5,6),
故选:C.
5.解:(﹣4,5),Q(﹣2,5)都在第二象限,
∵纵坐标都是5,
∴PQ∥x轴,
故选:A.
6.解:∵点C(﹣1,﹣2),D(﹣1,2),
∴CD=|﹣2﹣2|=4,
故选:D.
7.解:∵点A(﹣3,2)关于y轴对称的点是点B,
∴点B的坐标是(3,2),
∵点B关于x轴对称的点是点C,
∴点C的坐标是(3,﹣2).
故选:C.
8.解:由题意得:m+1=3m﹣5,或m+1+3m﹣5=0,
解得:m=3或m=1;
当m=3时,点B的坐标是(4,4);
当m=1时,点B的坐标是(2,﹣2).
所以点B的坐标为(4,4)或(2,﹣2).
故选:B.
9.解:过P点作PD⊥x轴,垂足为D,
由A(﹣,0)、B(0,1),得OA=,OB=1,
∵△ABC为等边三角形,
由勾股定理,得AB==2,
∴S△ABC=×2×=,
又∵S△ABP=S△AOB+S梯形BODP﹣S△ADP
=××1+×(1+a)×3﹣×(+3)×a,
=,
由2S△ABP=S△ABC,得=,
∴a=.
故选:C.
10.解:A、6排10座,物体的位置明确,故本选项不符合题意;
B、东经118°,北纬40°,物体的位置明确,故本选项不符合题意;
C、中山北路30号,物体的位置明确,故本选项不符合题意;
D、东北方向,只确定方向,不确定距离,即无法确定物体位置,故本选项符合题意.
故选:D.
11.解:点P(﹣5,3)到y轴的距离是|﹣5|=5,
故答案为:5.
12.解:∵点P(a﹣1,a+1)在y轴上,
∴a﹣1=0,
解得:a=1.
故答案为:1.
13.解:∵x2≥0,
∴﹣x2≤0,
∴﹣x2﹣1<0,
∴点P(﹣x2﹣1,2)在第二象限.
故答案为:二.
14.解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
15.解:∵点M(3,﹣2),MN∥x轴,
∴点N的纵坐标y=﹣2,
点N在点M的左边时,点N的横坐标为3﹣4=﹣1,
点N在点M的右边时,点N的横坐标为3+4=7,
所以,点N的坐标为(﹣1,﹣2)或(7,﹣2).
故答案为:(﹣1,﹣2)或(7,﹣2).
16.解:建立如图所示的直角坐标系,
教学楼的坐标是(﹣2,1).
17.解:(1)如图所示:△ABC的面积是:3×4﹣;
故答案为:4;
(2)点D与点C关于原点对称,则点D的坐标为:(﹣4,﹣3);
故答案为:(﹣4,﹣3);
(3)∵P为x轴上一点,△ABP的面积为4,
∴BP=8,
∴点P的横坐标为:2+8=10或2﹣8=﹣6,
故P点坐标为:(10,0)或(﹣6,0).
18.解:以D为坐标原点,OC和AD所在直线为x轴和y轴建立直角坐标系,
A的坐标是(0,4),B的坐标是(6,4),C的坐标是(6,0),D的坐标是(0,0);
作EG⊥CD交AB于点F.
∵AE=BE,
∴AF=AB=×6=3,
在直角△AEF中,EF===4,
则EG=4+4=8,
则E的坐标是(3,8).
19.解:坐标平面内各点的坐标A(﹣5,0),B(0,﹣3),C(5,﹣2),D(3,2),E(0,2),F(﹣3,4),
故答案为:﹣5,0;0,﹣3;5,﹣2;3,2;0,2;﹣3,4.
20.解:如图所示,以B为坐标原点,BC所在直线为x轴,过点B且垂直于x轴的直线为y轴建立平面直角坐标系,则
A(﹣2,3),B(0,0),D(6,1),E(5,3),F(3,2),G(1,5).
21.解:(1)∵点A在y轴上,
∴点A的横坐标为0,
而点A位于原点上方,距离原点2个单位长度,
∴点A的纵坐标为2,
∴点A的坐标为(0,2);
(2)点B在x轴上,
∴点B的纵坐标为0,
而点A位于原点右侧,距离原点1个单位长度,
∴点B的横坐标为1,∴点B的纵坐标为(1,0);
(3)∵点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度,
∴点C的坐标为(2,2);
(4)∵点D在下轴上方,y轴左侧,距离每条坐标轴都是3个单位长度,
∴点D的坐标为(﹣3,﹣3);
(5)∵点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度,
∴点E的坐标为(4,﹣2).
22.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,∴△ABC为等腰三角形.
23.解:(1)如图,点A,点C即为所求;
(2)S△ABC=×8×4=16;故答案为:16.
(3)如图,满足条件的点D的坐标为(0,4)或(0,﹣4).
故答案为:(0,4)或(0,﹣4).
24.解:(1)过点B,A分别作BF,AE垂直于x轴,所以四边形的面积=×3×6+×(6+8)×9+×2×8=80;
(2)根据平移的性质可知,平移后的图形形状和大小不变,所以所得的四边形面积是80.
25.解:(1)∵|a+2|+(b﹣4)2=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4;
故答案为:﹣2,4;
(2)如图1,过M作CE⊥x轴于E,
∵A(﹣2,0),B(4,0),
∴AB=6,
∵在第三象限内有一点M(﹣3,m),
∴ME=|m|=﹣m,
∴S△ABC=AB ME=×6×(﹣m)=﹣3m;
(3)当m=﹣3时,M(﹣3,﹣3),此时点M到x轴的距离是3.
∵在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,
∴点P到x轴的距离是3,
∴如图2,符合条件的坐标是:P(0,﹣3)或P′(0,3).
26.解:(1)∵A点的坐标为(4,0),C点的坐标为(0,6),
∴OA=4,OC=6,
∴点B(4,6);
故答案为:4,6.
(2)如图所示,
∵点P移动了4秒时的距离是2×4=8,
∴点P的坐标为(2,6);
(3)点P到x轴距离为5个单位长度时,点P的纵坐标为5,
若点P在OC上,则OP=5,
t=5÷2=2.5秒,
若点P在AB上,则OP=OC+BC+BP=6+4+(6﹣5)=11,
t=11÷2=5.5秒,
综上所述,点P移动的时间为2.5秒或5.5秒.
27.解:(1)由题意可得,
(2)由(1)中的平面直角坐标系可得,
校门口的坐标是(1,0),信息楼的坐标是(1,﹣2),综合楼的坐标是(﹣5,﹣3),实验楼的坐标是(﹣4,0);
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置,如下图所示,
28.解:(1)∵(a﹣2)2+=0,
∴a=2,b=3,
∵|c﹣4|≤0,
∴c=4;
(2)由(1)得A(0,2),
∵点P(m,1)在第二象限,
∴P到线段AO的距离为|m|,
∴S△AOP=×2 |m|=|m|,
∵m<0,
∴S△AOP=﹣m;
(3)存在点P(﹣6,1),使△AOP的面积与△ABC的面积相等,
理由如下:由(1)得,B(3,0),C(3,4),
∴|BC|=4,点A到BC的距离为3,
∴S△ABC=×3×4=6,
∵△AOP的面积与△ABC的面积相等,
∴﹣m=6,解得m=﹣6,
∴存在点P(﹣6,1),使△AOP的面积与△ABC的面积相等.
1.点M(2,3)关于x轴对称点的坐标为( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(3,﹣2)
2.以下点在第二象限的是( )
A.(0,0) B.(3,﹣5) C.(﹣1,9) D.(﹣2,﹣1)
3.如图,在平面直角坐标系中,△ABC关于直线m(直线m上各点的横坐标都为1)对称,点C的坐标为(4,1),则点B的坐标为( )
A.(﹣2,1) B.(﹣3,1) C.(﹣2,﹣1) D.(2,1)
4.在教室里,如果用(3,2)表示3排2列,那么5排6列可以表示为( )
A.(5,11) B.(11,6) C.(5,6) D.(6,5)
5.已知点P(﹣4,5),Q(﹣2,5),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于x轴 D.以上都不正确
6.已知点C(﹣1,﹣2),D(﹣1,2),则线段CD的长是( )
A.1 B.2 C.3 D.4
7.若点A(﹣3,2)关于y轴对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )
A.(3,2) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
8.若点B(m+1,3m﹣5)到x轴的距离与到y轴的距离相等,则点B的坐标是( )
A.(4,4)或(2,2) B.(4,4)或(2,﹣2)
C.(2,﹣2) D.(4,4)
9.如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且在直线AB的下方,满足2S△ABP=S△ABC,则a的值为( )
A. B. C. D.2
10.下列数据不能确定物体位置的是( )
A.6排10座 B.东经118°,北纬40°
C.中山北路30号 D.东北方向
11.点(﹣5,3)到y轴上的距离是 .
12.在平面直角坐标系中,点P(a﹣1,a+1)在y轴上,则a的值是 .
13.点P(﹣x2﹣1,2)在第 象限.
14.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),∠OCB=90°且OC=BC,则点C关于y轴对称的点的坐标是 .
15.已知点M(3,﹣2),它与点N(x,y)在同一条平行于x轴的直线上,且MN=4,那么点N的坐标是 .
16.如图,若实验楼的坐标是(1,﹣2),图书馆的坐标是(1,3),则教学楼的坐标是 .
17.如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若点D与点C关于原点对称,则点D的坐标为 ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
18.如图所示,在长方形ABCD中,已知AB=6,AD=4,在长方形ABCD外画△ABE,使AE=BE=5,请建立适当的平面直角坐标系,并求出各顶点的坐标.
19.已知:如图,写出坐标平面内各点的坐标.
A( , );B( , );
C( , );D( , );
E( , );F( , ).
20.建立平面直角坐标系,使点C的坐标为(4,0),写出点A、B、D、E、F、G的坐标.
21.在平面直角坐标系中,分别根据下列条件,求出各点的坐标.
(1)点A在y轴上,位于原点上方,距离原点2个单位长度;
(2)点B在x轴上,位于原点右侧,距离原点1个单位长度;
(3)点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
(4)点D在x轴下方,y轴左侧,距离每条坐标轴都是3个单位长度;
(5)点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度.
22.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
23.如图,在直角坐标平面内,已知点A的坐标(﹣4,0),点A关于y轴对称的点为点C.
(1)请在网格图中标出点A和点C.
(2)△ABC的面积是 ;
(3)在y轴上找一点D,使S△ACD=S△ABC,请直接写出点D的坐标 .
24.如图,四边形ABCD各个顶点的坐标分别为(﹣2,8),(﹣11,6),(﹣14,0),(0,0).
(1)确定这个四边形的面积,你是怎么做的?
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
25.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
26.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
(1)写出B点的坐标( );
(2)当点P移动了4秒时,描出此时P点的位置,并写出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
27.如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
28.如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)(b,c)(如图所示),其中a,b,c满足关系式(a﹣2)2+=0,|c﹣4|≤0.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,1),请用含m的代数式表示△AOP的面积;
(3)在(2)的条件下,是否存在点P,使△AOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.解:点M(2,3)关于x轴对称点的坐标为(2,﹣3),
故选:C.
2.解:A.(0,0)在原点,故本选项不合题意;
B.(3,﹣5)在第四象限,故本选项不合题意;
C.(﹣1,9)在第二象限,故本选项符合题意;
D.(﹣2,﹣1)在第三象限,故本选项不合题意;
故选:C.
3.解:∵△ABC关于直线m(直线m上各点的横坐标都为1)对称,
∴C,B关于直线m对称,即关于直线x=1对称,
∵点C的坐标为(4,1),
∴=1,
解得:x=﹣2,
则点B的坐标为:(﹣2,1).
故选:A.
4.解:用(3,2)表示3排2列,
那么5排6列应先表示排,再表示列,即(5,6),
故选:C.
5.解:(﹣4,5),Q(﹣2,5)都在第二象限,
∵纵坐标都是5,
∴PQ∥x轴,
故选:A.
6.解:∵点C(﹣1,﹣2),D(﹣1,2),
∴CD=|﹣2﹣2|=4,
故选:D.
7.解:∵点A(﹣3,2)关于y轴对称的点是点B,
∴点B的坐标是(3,2),
∵点B关于x轴对称的点是点C,
∴点C的坐标是(3,﹣2).
故选:C.
8.解:由题意得:m+1=3m﹣5,或m+1+3m﹣5=0,
解得:m=3或m=1;
当m=3时,点B的坐标是(4,4);
当m=1时,点B的坐标是(2,﹣2).
所以点B的坐标为(4,4)或(2,﹣2).
故选:B.
9.解:过P点作PD⊥x轴,垂足为D,
由A(﹣,0)、B(0,1),得OA=,OB=1,
∵△ABC为等边三角形,
由勾股定理,得AB==2,
∴S△ABC=×2×=,
又∵S△ABP=S△AOB+S梯形BODP﹣S△ADP
=××1+×(1+a)×3﹣×(+3)×a,
=,
由2S△ABP=S△ABC,得=,
∴a=.
故选:C.
10.解:A、6排10座,物体的位置明确,故本选项不符合题意;
B、东经118°,北纬40°,物体的位置明确,故本选项不符合题意;
C、中山北路30号,物体的位置明确,故本选项不符合题意;
D、东北方向,只确定方向,不确定距离,即无法确定物体位置,故本选项符合题意.
故选:D.
11.解:点P(﹣5,3)到y轴的距离是|﹣5|=5,
故答案为:5.
12.解:∵点P(a﹣1,a+1)在y轴上,
∴a﹣1=0,
解得:a=1.
故答案为:1.
13.解:∵x2≥0,
∴﹣x2≤0,
∴﹣x2﹣1<0,
∴点P(﹣x2﹣1,2)在第二象限.
故答案为:二.
14.解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
15.解:∵点M(3,﹣2),MN∥x轴,
∴点N的纵坐标y=﹣2,
点N在点M的左边时,点N的横坐标为3﹣4=﹣1,
点N在点M的右边时,点N的横坐标为3+4=7,
所以,点N的坐标为(﹣1,﹣2)或(7,﹣2).
故答案为:(﹣1,﹣2)或(7,﹣2).
16.解:建立如图所示的直角坐标系,
教学楼的坐标是(﹣2,1).
17.解:(1)如图所示:△ABC的面积是:3×4﹣;
故答案为:4;
(2)点D与点C关于原点对称,则点D的坐标为:(﹣4,﹣3);
故答案为:(﹣4,﹣3);
(3)∵P为x轴上一点,△ABP的面积为4,
∴BP=8,
∴点P的横坐标为:2+8=10或2﹣8=﹣6,
故P点坐标为:(10,0)或(﹣6,0).
18.解:以D为坐标原点,OC和AD所在直线为x轴和y轴建立直角坐标系,
A的坐标是(0,4),B的坐标是(6,4),C的坐标是(6,0),D的坐标是(0,0);
作EG⊥CD交AB于点F.
∵AE=BE,
∴AF=AB=×6=3,
在直角△AEF中,EF===4,
则EG=4+4=8,
则E的坐标是(3,8).
19.解:坐标平面内各点的坐标A(﹣5,0),B(0,﹣3),C(5,﹣2),D(3,2),E(0,2),F(﹣3,4),
故答案为:﹣5,0;0,﹣3;5,﹣2;3,2;0,2;﹣3,4.
20.解:如图所示,以B为坐标原点,BC所在直线为x轴,过点B且垂直于x轴的直线为y轴建立平面直角坐标系,则
A(﹣2,3),B(0,0),D(6,1),E(5,3),F(3,2),G(1,5).
21.解:(1)∵点A在y轴上,
∴点A的横坐标为0,
而点A位于原点上方,距离原点2个单位长度,
∴点A的纵坐标为2,
∴点A的坐标为(0,2);
(2)点B在x轴上,
∴点B的纵坐标为0,
而点A位于原点右侧,距离原点1个单位长度,
∴点B的横坐标为1,∴点B的纵坐标为(1,0);
(3)∵点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度,
∴点C的坐标为(2,2);
(4)∵点D在下轴上方,y轴左侧,距离每条坐标轴都是3个单位长度,
∴点D的坐标为(﹣3,﹣3);
(5)∵点E在x轴下方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度,
∴点E的坐标为(4,﹣2).
22.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,∴△ABC为等腰三角形.
23.解:(1)如图,点A,点C即为所求;
(2)S△ABC=×8×4=16;故答案为:16.
(3)如图,满足条件的点D的坐标为(0,4)或(0,﹣4).
故答案为:(0,4)或(0,﹣4).
24.解:(1)过点B,A分别作BF,AE垂直于x轴,所以四边形的面积=×3×6+×(6+8)×9+×2×8=80;
(2)根据平移的性质可知,平移后的图形形状和大小不变,所以所得的四边形面积是80.
25.解:(1)∵|a+2|+(b﹣4)2=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4;
故答案为:﹣2,4;
(2)如图1,过M作CE⊥x轴于E,
∵A(﹣2,0),B(4,0),
∴AB=6,
∵在第三象限内有一点M(﹣3,m),
∴ME=|m|=﹣m,
∴S△ABC=AB ME=×6×(﹣m)=﹣3m;
(3)当m=﹣3时,M(﹣3,﹣3),此时点M到x轴的距离是3.
∵在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,
∴点P到x轴的距离是3,
∴如图2,符合条件的坐标是:P(0,﹣3)或P′(0,3).
26.解:(1)∵A点的坐标为(4,0),C点的坐标为(0,6),
∴OA=4,OC=6,
∴点B(4,6);
故答案为:4,6.
(2)如图所示,
∵点P移动了4秒时的距离是2×4=8,
∴点P的坐标为(2,6);
(3)点P到x轴距离为5个单位长度时,点P的纵坐标为5,
若点P在OC上,则OP=5,
t=5÷2=2.5秒,
若点P在AB上,则OP=OC+BC+BP=6+4+(6﹣5)=11,
t=11÷2=5.5秒,
综上所述,点P移动的时间为2.5秒或5.5秒.
27.解:(1)由题意可得,
(2)由(1)中的平面直角坐标系可得,
校门口的坐标是(1,0),信息楼的坐标是(1,﹣2),综合楼的坐标是(﹣5,﹣3),实验楼的坐标是(﹣4,0);
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置,如下图所示,
28.解:(1)∵(a﹣2)2+=0,
∴a=2,b=3,
∵|c﹣4|≤0,
∴c=4;
(2)由(1)得A(0,2),
∵点P(m,1)在第二象限,
∴P到线段AO的距离为|m|,
∴S△AOP=×2 |m|=|m|,
∵m<0,
∴S△AOP=﹣m;
(3)存在点P(﹣6,1),使△AOP的面积与△ABC的面积相等,
理由如下:由(1)得,B(3,0),C(3,4),
∴|BC|=4,点A到BC的距离为3,
∴S△ABC=×3×4=6,
∵△AOP的面积与△ABC的面积相等,
∴﹣m=6,解得m=﹣6,
∴存在点P(﹣6,1),使△AOP的面积与△ABC的面积相等.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
