2021-2022学年北师大版八年级数学上册第4章一次函数 期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第4章一次函数 期末综合复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 372.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 15:37:33 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学上册《第4章一次函数》期末综合复习训练(附答案)
1.下面关系式中x与y不成正比例的是( )
A.x×=3 B.5x=6y C.4÷x=y D.x=y
2.已知变量y与x的关系满足下表,那么能反映y与x之间的函数关系的解析式是( )
x … ﹣2 ﹣1 0 1 2 …
y … 4 3 2 1 0 …
A.y=﹣2x B.y=x+4 C.y=﹣x+2 D.y=2x﹣2
3.已知直线y=kx+b经过点(2,1),则方程kx+b=1的解为( )
A.x=0 B.x=1 C.x=2 D.x=±2
4.汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是( )
A.S=120﹣30t(0≤t≤4) B.S=30t(0≤t≤4)
C.S=120﹣30t(t>0) D.S=30t(t=4)
5.若直线y=kx+b经过第二、三、四象限,则直线y=﹣bx+k不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.一次函数y1=ax+b与一次函数y2=bx﹣a在同一平面直角坐标系中的图象大致是( )
A.B.C.D.
7.一次函数y=kx+b的图象如图所示,则下列选项中错误的说法是( )
A.kb<0 B.当x<0时,y>b
C.若点A(﹣1,y1) 与B(2,y2)都在直线y=kx+b上,则y1>y2
D.将函数图象向左平移1个单位后,图象恰好经过坐标原点,则k=b
8.在平面直角坐标系中,将一次函数y=x﹣的图象沿x轴向左平移m(m≥0)个单位后经过原点O,则m的值为( )
A. B. C.2 D.
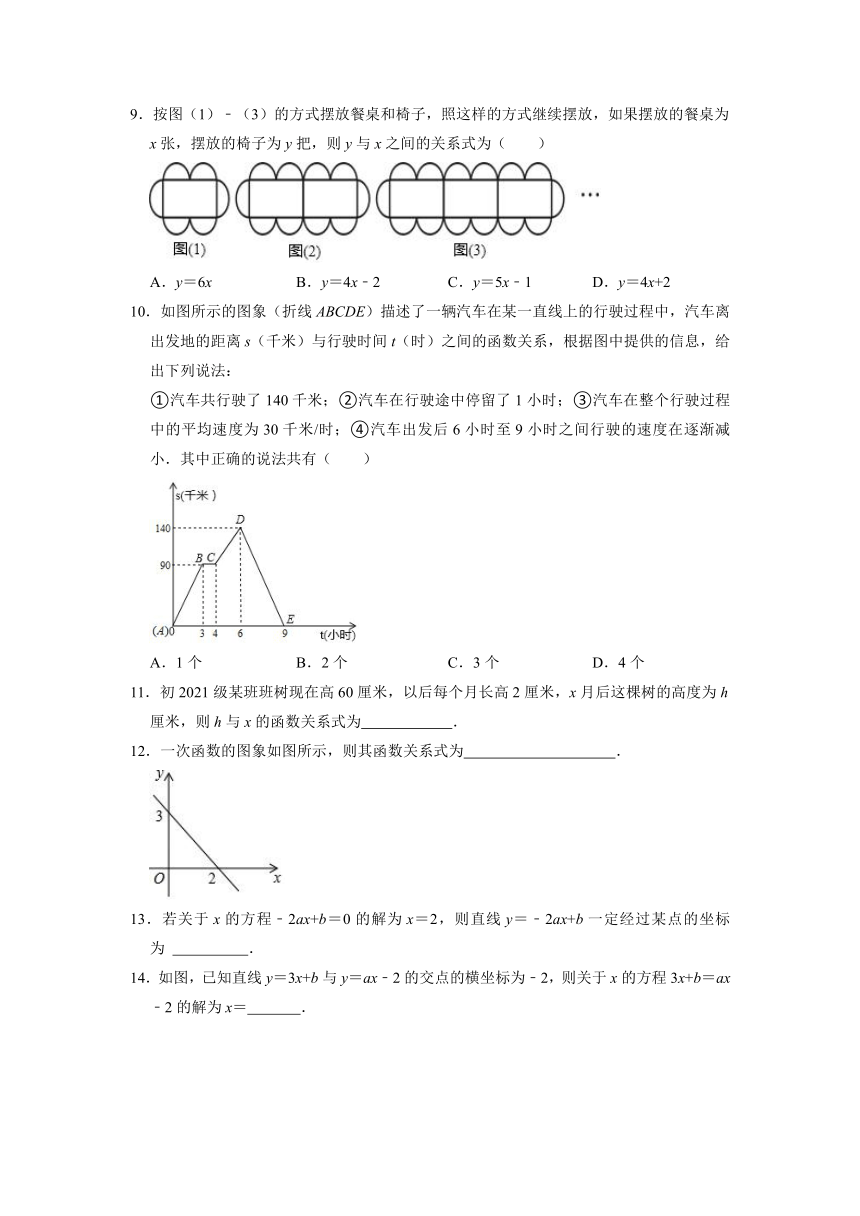
9.按图(1)﹣(3)的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为x张,摆放的椅子为y把,则y与x之间的关系式为( )
A.y=6x B.y=4x﹣2 C.y=5x﹣1 D.y=4x+2
10.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
11.初2021级某班班树现在高60厘米,以后每个月长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .
12.一次函数的图象如图所示,则其函数关系式为 .
13.若关于x的方程﹣2ax+b=0的解为x=2,则直线y=﹣2ax+b一定经过某点的坐标为 .
14.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的方程3x+b=ax﹣2的解为x= .
15.汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为y= ,该汽车最多可行驶 小时.
16.某工厂日夜连续加班,计划为灾区生产m顶帐篷,生产过程中的剩余生产任务y(顶)与已用生产时间x(时)之间的关系如图所示.则变量y与x之间的关系式是 .
17.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为 千米.
18.汽车油箱中余油量Q(升)与它的行驶时间t(小时)之间的为如图所示的一次函数关系,则其解析式为 .t的范围是 .
19.为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费为y元.
(1)当月用电量不超过200时,y与x的函数关系式为 ,当月用电量超过200度时,y与x的函数关系式为 .
(2)小新家十月份用电量为160度,求本月应交电费多少元?
(3)小明家十月份交纳电费117元,求本月用电多少度?
20.如图,在平面直角坐标系内,点B是x轴上的点,点A是y轴上的点,将△AOB沿直线AB翻折使点O落在C点处,过C点作CD⊥y轴交y轴于点D,已知C(4,8).
(1)直接写出A、B两点的坐标;
(2)若在x轴上存在某点N,使得以A、B、C.N四点为顶点的四边形面积为40,求N点的坐标;
(3)若P点是y轴上一动点,当△PAB为等腰三角形时,请直接写出点P的坐标.
21.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.
(1)求直线AB的解析式;
(2)当△OPB的面积是△OBC的面积的时,求出这时点P的坐标;
(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
22.过点C(﹣6,c)的直线y=2x+6,交x轴于点A,交y轴于点B.
(1)点A坐标 ;点B坐标 ;点C坐标 ;
(2)如图,在BC左侧有一点D,使△BCD是等腰直角三角形,并且BD=CD,求点D的坐标;
(3)过点A的直线AE把△BOC的面积分为1:2,交△BOC另一边于点E,求点E的坐标.
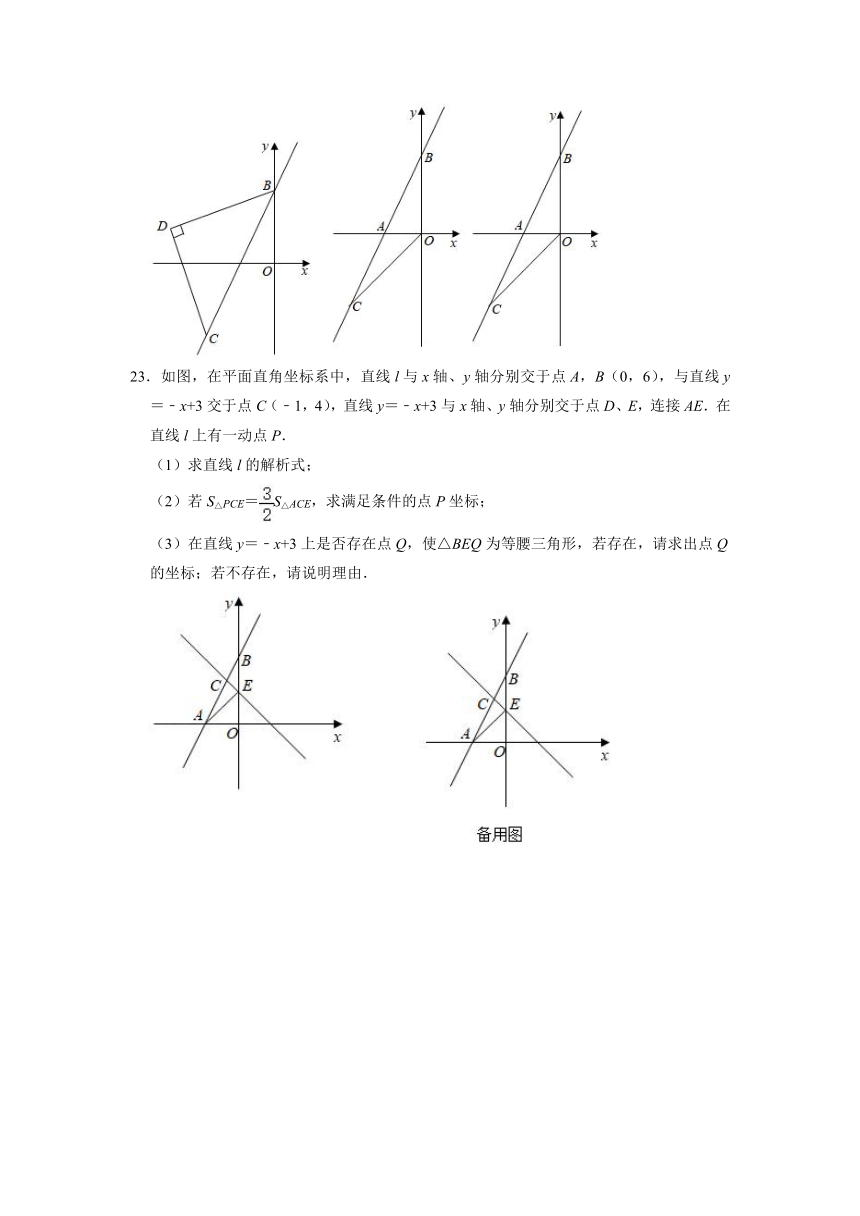
23.如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A,B(0,6),与直线y=﹣x+3交于点C(﹣1,4),直线y=﹣x+3与x轴、y轴分别交于点D、E,连接AE.在直线l上有一动点P.
(1)求直线l的解析式;
(2)若S△PCE=S△ACE,求满足条件的点P坐标;
(3)在直线y=﹣x+3上是否存在点Q,使△BEQ为等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案
1.解:A、∵x×=3,∴y=,∴x与y成正比例,故本选项不符合题意;
B、∵5x=6y,∴y=x,∴x与y成正比例,故本选项不符合题意;
C、∵4÷x=y,∴y=,∴x与y不成正比例,故本选项符合题意;
D、∵x=y,∴y=2x,∴x与y成正比例,故本选项不符合题意.
故选:C.
2.解:设y与x之间的函数关系的解析式是y=kx+b(k≠0),
把(1,1),(0,2)代入得,
解得,
所以,y与x之间的函数关系的解析式是y=﹣x+2.
经检验,其余各点都满足函数的解析式,
故选:C.
3.解:∵直线y=kx+b经过点(2,1),
∴当x=2时,1=kx+b,
∴方程kx+b=1的解为x=2,
故选:C.
4.解:汽车行驶路程为:30t,
∴车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是:S=120﹣30t(0≤t≤4).
故选:A.
5.解:∵直线y=kx+b经过第二、三、四象限,
∴k<0,b<0,
∴﹣b>0,
∴直线y=﹣bx+k经过第一、三、四象限,不经过第二象限,
故选:B.
6.解:A、由y1的图象可知,a>0,b>0;由y2的图象可知,b<0,﹣a>0,即a<0,两结论矛盾,故错误;
B、由y1的图象可知,a>0,b<0;由y2的图象可知,b<0,﹣a>0,即a<0,两结论矛盾,故错误;
C、由y1的图象可知,a<0,b<0;由y2的图象可知,b<0,﹣a<0,即a>0,两结论相矛盾,故错误;
D、由y1的图象可知,a>0,b>0;由y2的图象可知,b>0,﹣a<0,即a>0,两结论符合,故正确.
故选:D.
7.解:A、观察一次函数图象发现,图象过第一、二、四象限,
∴k<0,b>0.
∴kb<0,故A正确;
B、结合函数图象能够发现,当x<1时,y>0,故B正确;
C、∵k<0,
∴函数值y随x的增大而减少,
∵﹣1<2,
∴y1>y2,故C正确;
D、将函数图象向左平移1个单位后得到y=k(x+1)+b=kx+k+b,
∵经过原点,
∴k+b=0,故D错误.
故选:D.
8.解:将一次函数y=x﹣的图象沿x轴向左平移m(m≥0)个单位后得到y=(x+m)﹣,
把(0,0)代入,得到:0=m﹣,
解得m=.
故选:D.
9.解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
∵多一张餐桌,多放4把椅子,
∴第x张餐桌共有y=6+4(x﹣1)=4x+2.
故选:D.
10.解:汽车从出发地到目的地走了140千米,又回到出发地因而共行驶了280千米,故①错误;
汽车在行驶途中停留了4﹣3=1小时,故②正确;
汽车在整个行驶过程中的平均速度为:280÷9=(千米/时),故③错误;
汽车出发后6小时至9小时之间行驶的速度不变,故④错误.
综上所述,正确的只有②.
故选:A.
11.解:依题意有:h=60+2x,
故答案为:h=60+2x.
12.解:如图所示:设解析式为:y=kx+b,将(0,3),(2,0)代入得:
,
解得:,
故此函数的解析式为:y=﹣x+3.
故答案为:y=﹣x+3.
13.解:由方程的解可知:当x=2时,﹣4a+b=0,即b=4a,
∴直线为y=﹣2ax+4a,
当y=0时,x=2.
故答案为:(2,0).
14.解:∵直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
∴当x=﹣2时,3x+b=ax﹣2,
∴关于x的方程3x+b=ax﹣2的解为x=﹣2.
故答案为﹣2.
15.解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=40﹣5x,
当y=0时,40﹣5x=0,
解得:x=8,
即汽车最多可行驶8小时.
16.解:设相应的直线解析式为y=kx+b,
∵(30,400),(50,0)适合这个函数解析式,
∴30k+b=400,50k+b=0,
解得k=﹣20,b=1000,
∴y=﹣20x+1000(0≤x≤50).
17.解:由题,图可知甲走的是C路线,乙走的是D路线,
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=,b=3,
所以sD=t+3,
当t=3时,sC﹣sD=6﹣=.
18.解:依题意设Q=at+b(a、b为常数)
把t=0,Q=60和t=4,Q=40代入函数关系式,得
解得
所以,Q=﹣5t+60;
∵Q=﹣5t+60≥0,
∴0≤t≤12.
19.解:(1)当0≤x≤200时,y与x的函数解析式是y=0.55x;
当x>200时,y与x的函数解析式是y=0.55×200+0.7(x﹣200),即y=0.7x﹣30;
(2)小新家十月份用电160度,月用电量没超过200度,
∴应交电费为:0.55×160=88(元),
(3)由题意可知,用电两是200度时,电费为110元,
∵小明家十月份的电费超过110元,
∴把y=117代入y=0.7x﹣30中,得x=210.
答:小明家十月份用电210度.
20.解:(1)如图1,作CF⊥OB于点F,连接OC,
∵C(4,8),CD⊥y轴于点D,
∴D(0,8),F(4,0),
∴CD=OF=4,OD=CF=8,
由折叠得CA=OA,
∴AD=8﹣OA=8﹣CA,
∵∠ADC=90°,
∴CA2=AD2+CD2,
∴OA2=(8﹣OA)2+42,
解得OA=5,
∴A(0,5),
∵∠CFB=90°,
∴CB2=BF2+CF2,
∵CB=OB,BF=OB﹣4,CF=8,
∴OB2=(OB﹣4)2+82,
解得OB=10,
∴B(10,0).
(2)设点N的坐标为(m,0),
∵∠AOB=90°,OA=5,OB=10,
∴S△ACB=S△AOB=×5×10=25,
如图1,点N在点B的左侧,则BN=10﹣m,
∵S四边形ANBC=40,
∴×5(10﹣m)+25=40,
解得m=4,
∴N(4,0);
如图2,点N在点B的右侧,则BN=m﹣10,
∵S四边形ABNC=40,
∴×8(m﹣10)+25=40,
解得,m=,
∴N(,0),
综上所述,点N的坐标为(4,0)或(,0).
(3)如图3,点P在点A的下方,
∵∠AOB=90°,A(0,5),B(10,0),
∴AB==,
当AP=AB=时,则yp=,
∴P(0,);
当PB=AB时,则OP=OA=5,
∴P(0,﹣5);
当AP=BP时,则BP=5+OP,
∵∠POB=90°,
∴BP2=OP2+OB2,
∴(5+OP)2=OP2+102,
解得OP=,
∴P(0,);
如图4,点P在点A的上方,则AP=AB=,
∴yp=,
∴P(0,),
综上所述,点P的坐标为(0,)或(0,﹣5)或(0,)或(0,).
21.解:(1)∵点A的坐标为(0,6),
∴设直线AB的解析式为y=kx+6,
∵点C(2,4)在直线AB上,
∴2k+6=4,
∴k=﹣1,
∴直线AB的解析式为y=﹣x+6;
(2)由(1)知,直线AB的解析式为y=﹣x+6,
令y=0,
∴﹣x+6=0,
∴x=6,
∴B(6,0),
∴S△OBC=OB yC=12,
∵△OPB的面积是△OBC的面积的,
∴S△OPB=×12=3,
设P的纵坐标为m,
∴S△OPB=OB m=3m=3,
∴m=1,
∵C(2,4),
∴直线OC的解析式为y=2x,
当点P在OC上时,x=,
∴P(,1),
当点P在BC上时,x=6﹣1=5,
∴P(5,1),
即:点P(,1)或(5,1);
(3)∵△OBP是直角三角形,
∴∠OPB=90°,
①当点P在OC上时,如图,过点C作CH⊥x轴于H,
∵C(2,4),
∴CH=4,OC=2
∴S△OBC=OB CH=OC BP,
∴BP===,
由(2)知,直线OC的解析式为y=2x①,
设点P的坐标为(m,2m),
∵B(6,0),
∴BP2=(m﹣6)2+4m2=,
∴m=
∴P(,),
②当点P在BC上时,同①的方法,
∴P(3,3),
即:点P的坐标为(,)或(3,3).
22.解:(1)令y=0,0=﹣2x+6,x=﹣3,则A(﹣3,0);
令x=0,y=6,则B(0,6);
把x=﹣6带入直线关系式得:y=﹣2×(﹣6)+6=﹣6,
则D(﹣6,﹣6),
故答案为:(﹣3,0),(0,6)、(﹣6,﹣6);
(2)如图,过点D作DE⊥y于点E,过点C作CF⊥DE与点F,交x轴于点H,
则∠FDC+∠FCD=90°,∠CFD=∠DEB=90°
∵△BDC为等腰直角三角形,BD=CD,
∴∠BDC=90°,
∴∠BDE+∠CDF=90°,
∴∠BDE=∠DCF
∵∠CFD=∠DEB,∠BDE=∠DCF,BD=CD,
∴△BDE≌△DCF(AAS),
∴DE=CF,BE=DF,
∵C(﹣6,﹣6),
∴CH=FE=6,
∴FH=DF=BE,
∵B(0,6),
∴BO=6,
∴EO=BE=3,
∴DE=FE+DF=6+3=9,
∴D(﹣9,3);
(3)△BOC的面积=×BO×|xC|=×6×6=18,
同理可得:S△AOB=S△AOC=9,
①当点E(E′)在边BO上时,
由题意得:S△BAE′=S△BOC=×18=6=×BE′×AO=×BE′×3,解得BE′=4,
而点B(0,6),
故点E′的坐标为(0,2);
②当点E在边CO上时,
由题意得:S△AEC=S△BOC=×18=6,
而S△AOC=9,故S△AEO=9﹣6=3=×AO×|yE|=×3×|yE|,解得yE=﹣2,
由点O、C的坐标知,直线OC的表达式为y=x,
当y=﹣2时,y=x=﹣2,
故点E的坐标为(﹣2,﹣2),
故点E的坐标为(0,2)或(﹣2,﹣2).
23.解:(1)直线l过点B,则设直线l的表达式为y=kx+6,
将点C的坐标代入上式得:4=﹣k+6,解得k=2,
故直线l的表达式为y=2x+6①;
(2)对于y=2x+6,令y=2x+6=0,解得x=﹣3,故点A(﹣3,0),
对于y=﹣x+3,令x=0,则y=3,故点E(0,3),
①当点P在直线CD的上方时,
过点A作直线k∥CD交y轴于点H,作直线m∥CD交y轴于点M,
∵S△PCE=S△ACE,则直线m与直线CD之间的距离和直线k与直线CD之间的距离为3:2,
则ME=EH,
∵直线k∥CD,设直线k的表达式为y=﹣x+b,将点A的坐标代入上式得:0=3+b,解得b=﹣3,
故点H(0,﹣3),
∵ME=EH=×(3+3)=9,
故点M的坐标为(0,12),
同理可得,直线m的表达式为y=﹣x+12②,
联立①②并解得,
故点P(2,10);
②当点P在直线CD的下方时,
同理可得,点P(﹣4,﹣2);
综上,点P的坐标为(2,10)或(﹣4,﹣2);
(3)存在,理由:
设点Q(m,3﹣m),
由点B、E、Q的坐标得:BQ2=m2+(3﹣m﹣6)2,BE2=9,QE2=2m2,
当BQ=BE时,即m2+(3﹣m﹣6)2=9,解得m=0(舍去)﹣3;
当BQ=EQ时,同理可得:m=﹣;
当BE=QE时,同理可得:m=±;
综上,点Q的坐标为(,3﹣)或(﹣,3+)或(﹣,)或(﹣3,6).
1.下面关系式中x与y不成正比例的是( )
A.x×=3 B.5x=6y C.4÷x=y D.x=y
2.已知变量y与x的关系满足下表,那么能反映y与x之间的函数关系的解析式是( )
x … ﹣2 ﹣1 0 1 2 …
y … 4 3 2 1 0 …
A.y=﹣2x B.y=x+4 C.y=﹣x+2 D.y=2x﹣2
3.已知直线y=kx+b经过点(2,1),则方程kx+b=1的解为( )
A.x=0 B.x=1 C.x=2 D.x=±2
4.汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是( )
A.S=120﹣30t(0≤t≤4) B.S=30t(0≤t≤4)
C.S=120﹣30t(t>0) D.S=30t(t=4)
5.若直线y=kx+b经过第二、三、四象限,则直线y=﹣bx+k不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.一次函数y1=ax+b与一次函数y2=bx﹣a在同一平面直角坐标系中的图象大致是( )
A.B.C.D.
7.一次函数y=kx+b的图象如图所示,则下列选项中错误的说法是( )
A.kb<0 B.当x<0时,y>b
C.若点A(﹣1,y1) 与B(2,y2)都在直线y=kx+b上,则y1>y2
D.将函数图象向左平移1个单位后,图象恰好经过坐标原点,则k=b
8.在平面直角坐标系中,将一次函数y=x﹣的图象沿x轴向左平移m(m≥0)个单位后经过原点O,则m的值为( )
A. B. C.2 D.
9.按图(1)﹣(3)的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为x张,摆放的椅子为y把,则y与x之间的关系式为( )
A.y=6x B.y=4x﹣2 C.y=5x﹣1 D.y=4x+2
10.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
11.初2021级某班班树现在高60厘米,以后每个月长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .
12.一次函数的图象如图所示,则其函数关系式为 .
13.若关于x的方程﹣2ax+b=0的解为x=2,则直线y=﹣2ax+b一定经过某点的坐标为 .
14.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的方程3x+b=ax﹣2的解为x= .
15.汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为y= ,该汽车最多可行驶 小时.
16.某工厂日夜连续加班,计划为灾区生产m顶帐篷,生产过程中的剩余生产任务y(顶)与已用生产时间x(时)之间的关系如图所示.则变量y与x之间的关系式是 .
17.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为 千米.
18.汽车油箱中余油量Q(升)与它的行驶时间t(小时)之间的为如图所示的一次函数关系,则其解析式为 .t的范围是 .
19.为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费为y元.
(1)当月用电量不超过200时,y与x的函数关系式为 ,当月用电量超过200度时,y与x的函数关系式为 .
(2)小新家十月份用电量为160度,求本月应交电费多少元?
(3)小明家十月份交纳电费117元,求本月用电多少度?
20.如图,在平面直角坐标系内,点B是x轴上的点,点A是y轴上的点,将△AOB沿直线AB翻折使点O落在C点处,过C点作CD⊥y轴交y轴于点D,已知C(4,8).
(1)直接写出A、B两点的坐标;
(2)若在x轴上存在某点N,使得以A、B、C.N四点为顶点的四边形面积为40,求N点的坐标;
(3)若P点是y轴上一动点,当△PAB为等腰三角形时,请直接写出点P的坐标.
21.如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.
(1)求直线AB的解析式;
(2)当△OPB的面积是△OBC的面积的时,求出这时点P的坐标;
(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
22.过点C(﹣6,c)的直线y=2x+6,交x轴于点A,交y轴于点B.
(1)点A坐标 ;点B坐标 ;点C坐标 ;
(2)如图,在BC左侧有一点D,使△BCD是等腰直角三角形,并且BD=CD,求点D的坐标;
(3)过点A的直线AE把△BOC的面积分为1:2,交△BOC另一边于点E,求点E的坐标.
23.如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A,B(0,6),与直线y=﹣x+3交于点C(﹣1,4),直线y=﹣x+3与x轴、y轴分别交于点D、E,连接AE.在直线l上有一动点P.
(1)求直线l的解析式;
(2)若S△PCE=S△ACE,求满足条件的点P坐标;
(3)在直线y=﹣x+3上是否存在点Q,使△BEQ为等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案
1.解:A、∵x×=3,∴y=,∴x与y成正比例,故本选项不符合题意;
B、∵5x=6y,∴y=x,∴x与y成正比例,故本选项不符合题意;
C、∵4÷x=y,∴y=,∴x与y不成正比例,故本选项符合题意;
D、∵x=y,∴y=2x,∴x与y成正比例,故本选项不符合题意.
故选:C.
2.解:设y与x之间的函数关系的解析式是y=kx+b(k≠0),
把(1,1),(0,2)代入得,
解得,
所以,y与x之间的函数关系的解析式是y=﹣x+2.
经检验,其余各点都满足函数的解析式,
故选:C.
3.解:∵直线y=kx+b经过点(2,1),
∴当x=2时,1=kx+b,
∴方程kx+b=1的解为x=2,
故选:C.
4.解:汽车行驶路程为:30t,
∴车距天津的路程S(千米)与行驶时间t(时)的函数关系及自变量的取值范围是:S=120﹣30t(0≤t≤4).
故选:A.
5.解:∵直线y=kx+b经过第二、三、四象限,
∴k<0,b<0,
∴﹣b>0,
∴直线y=﹣bx+k经过第一、三、四象限,不经过第二象限,
故选:B.
6.解:A、由y1的图象可知,a>0,b>0;由y2的图象可知,b<0,﹣a>0,即a<0,两结论矛盾,故错误;
B、由y1的图象可知,a>0,b<0;由y2的图象可知,b<0,﹣a>0,即a<0,两结论矛盾,故错误;
C、由y1的图象可知,a<0,b<0;由y2的图象可知,b<0,﹣a<0,即a>0,两结论相矛盾,故错误;
D、由y1的图象可知,a>0,b>0;由y2的图象可知,b>0,﹣a<0,即a>0,两结论符合,故正确.
故选:D.
7.解:A、观察一次函数图象发现,图象过第一、二、四象限,
∴k<0,b>0.
∴kb<0,故A正确;
B、结合函数图象能够发现,当x<1时,y>0,故B正确;
C、∵k<0,
∴函数值y随x的增大而减少,
∵﹣1<2,
∴y1>y2,故C正确;
D、将函数图象向左平移1个单位后得到y=k(x+1)+b=kx+k+b,
∵经过原点,
∴k+b=0,故D错误.
故选:D.
8.解:将一次函数y=x﹣的图象沿x轴向左平移m(m≥0)个单位后得到y=(x+m)﹣,
把(0,0)代入,得到:0=m﹣,
解得m=.
故选:D.
9.解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
∵多一张餐桌,多放4把椅子,
∴第x张餐桌共有y=6+4(x﹣1)=4x+2.
故选:D.
10.解:汽车从出发地到目的地走了140千米,又回到出发地因而共行驶了280千米,故①错误;
汽车在行驶途中停留了4﹣3=1小时,故②正确;
汽车在整个行驶过程中的平均速度为:280÷9=(千米/时),故③错误;
汽车出发后6小时至9小时之间行驶的速度不变,故④错误.
综上所述,正确的只有②.
故选:A.
11.解:依题意有:h=60+2x,
故答案为:h=60+2x.
12.解:如图所示:设解析式为:y=kx+b,将(0,3),(2,0)代入得:
,
解得:,
故此函数的解析式为:y=﹣x+3.
故答案为:y=﹣x+3.
13.解:由方程的解可知:当x=2时,﹣4a+b=0,即b=4a,
∴直线为y=﹣2ax+4a,
当y=0时,x=2.
故答案为:(2,0).
14.解:∵直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
∴当x=﹣2时,3x+b=ax﹣2,
∴关于x的方程3x+b=ax﹣2的解为x=﹣2.
故答案为﹣2.
15.解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=40﹣5x,
当y=0时,40﹣5x=0,
解得:x=8,
即汽车最多可行驶8小时.
16.解:设相应的直线解析式为y=kx+b,
∵(30,400),(50,0)适合这个函数解析式,
∴30k+b=400,50k+b=0,
解得k=﹣20,b=1000,
∴y=﹣20x+1000(0≤x≤50).
17.解:由题,图可知甲走的是C路线,乙走的是D路线,
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=,b=3,
所以sD=t+3,
当t=3时,sC﹣sD=6﹣=.
18.解:依题意设Q=at+b(a、b为常数)
把t=0,Q=60和t=4,Q=40代入函数关系式,得
解得
所以,Q=﹣5t+60;
∵Q=﹣5t+60≥0,
∴0≤t≤12.
19.解:(1)当0≤x≤200时,y与x的函数解析式是y=0.55x;
当x>200时,y与x的函数解析式是y=0.55×200+0.7(x﹣200),即y=0.7x﹣30;
(2)小新家十月份用电160度,月用电量没超过200度,
∴应交电费为:0.55×160=88(元),
(3)由题意可知,用电两是200度时,电费为110元,
∵小明家十月份的电费超过110元,
∴把y=117代入y=0.7x﹣30中,得x=210.
答:小明家十月份用电210度.
20.解:(1)如图1,作CF⊥OB于点F,连接OC,
∵C(4,8),CD⊥y轴于点D,
∴D(0,8),F(4,0),
∴CD=OF=4,OD=CF=8,
由折叠得CA=OA,
∴AD=8﹣OA=8﹣CA,
∵∠ADC=90°,
∴CA2=AD2+CD2,
∴OA2=(8﹣OA)2+42,
解得OA=5,
∴A(0,5),
∵∠CFB=90°,
∴CB2=BF2+CF2,
∵CB=OB,BF=OB﹣4,CF=8,
∴OB2=(OB﹣4)2+82,
解得OB=10,
∴B(10,0).
(2)设点N的坐标为(m,0),
∵∠AOB=90°,OA=5,OB=10,
∴S△ACB=S△AOB=×5×10=25,
如图1,点N在点B的左侧,则BN=10﹣m,
∵S四边形ANBC=40,
∴×5(10﹣m)+25=40,
解得m=4,
∴N(4,0);
如图2,点N在点B的右侧,则BN=m﹣10,
∵S四边形ABNC=40,
∴×8(m﹣10)+25=40,
解得,m=,
∴N(,0),
综上所述,点N的坐标为(4,0)或(,0).
(3)如图3,点P在点A的下方,
∵∠AOB=90°,A(0,5),B(10,0),
∴AB==,
当AP=AB=时,则yp=,
∴P(0,);
当PB=AB时,则OP=OA=5,
∴P(0,﹣5);
当AP=BP时,则BP=5+OP,
∵∠POB=90°,
∴BP2=OP2+OB2,
∴(5+OP)2=OP2+102,
解得OP=,
∴P(0,);
如图4,点P在点A的上方,则AP=AB=,
∴yp=,
∴P(0,),
综上所述,点P的坐标为(0,)或(0,﹣5)或(0,)或(0,).
21.解:(1)∵点A的坐标为(0,6),
∴设直线AB的解析式为y=kx+6,
∵点C(2,4)在直线AB上,
∴2k+6=4,
∴k=﹣1,
∴直线AB的解析式为y=﹣x+6;
(2)由(1)知,直线AB的解析式为y=﹣x+6,
令y=0,
∴﹣x+6=0,
∴x=6,
∴B(6,0),
∴S△OBC=OB yC=12,
∵△OPB的面积是△OBC的面积的,
∴S△OPB=×12=3,
设P的纵坐标为m,
∴S△OPB=OB m=3m=3,
∴m=1,
∵C(2,4),
∴直线OC的解析式为y=2x,
当点P在OC上时,x=,
∴P(,1),
当点P在BC上时,x=6﹣1=5,
∴P(5,1),
即:点P(,1)或(5,1);
(3)∵△OBP是直角三角形,
∴∠OPB=90°,
①当点P在OC上时,如图,过点C作CH⊥x轴于H,
∵C(2,4),
∴CH=4,OC=2
∴S△OBC=OB CH=OC BP,
∴BP===,
由(2)知,直线OC的解析式为y=2x①,
设点P的坐标为(m,2m),
∵B(6,0),
∴BP2=(m﹣6)2+4m2=,
∴m=
∴P(,),
②当点P在BC上时,同①的方法,
∴P(3,3),
即:点P的坐标为(,)或(3,3).
22.解:(1)令y=0,0=﹣2x+6,x=﹣3,则A(﹣3,0);
令x=0,y=6,则B(0,6);
把x=﹣6带入直线关系式得:y=﹣2×(﹣6)+6=﹣6,
则D(﹣6,﹣6),
故答案为:(﹣3,0),(0,6)、(﹣6,﹣6);
(2)如图,过点D作DE⊥y于点E,过点C作CF⊥DE与点F,交x轴于点H,
则∠FDC+∠FCD=90°,∠CFD=∠DEB=90°
∵△BDC为等腰直角三角形,BD=CD,
∴∠BDC=90°,
∴∠BDE+∠CDF=90°,
∴∠BDE=∠DCF
∵∠CFD=∠DEB,∠BDE=∠DCF,BD=CD,
∴△BDE≌△DCF(AAS),
∴DE=CF,BE=DF,
∵C(﹣6,﹣6),
∴CH=FE=6,
∴FH=DF=BE,
∵B(0,6),
∴BO=6,
∴EO=BE=3,
∴DE=FE+DF=6+3=9,
∴D(﹣9,3);
(3)△BOC的面积=×BO×|xC|=×6×6=18,
同理可得:S△AOB=S△AOC=9,
①当点E(E′)在边BO上时,
由题意得:S△BAE′=S△BOC=×18=6=×BE′×AO=×BE′×3,解得BE′=4,
而点B(0,6),
故点E′的坐标为(0,2);
②当点E在边CO上时,
由题意得:S△AEC=S△BOC=×18=6,
而S△AOC=9,故S△AEO=9﹣6=3=×AO×|yE|=×3×|yE|,解得yE=﹣2,
由点O、C的坐标知,直线OC的表达式为y=x,
当y=﹣2时,y=x=﹣2,
故点E的坐标为(﹣2,﹣2),
故点E的坐标为(0,2)或(﹣2,﹣2).
23.解:(1)直线l过点B,则设直线l的表达式为y=kx+6,
将点C的坐标代入上式得:4=﹣k+6,解得k=2,
故直线l的表达式为y=2x+6①;
(2)对于y=2x+6,令y=2x+6=0,解得x=﹣3,故点A(﹣3,0),
对于y=﹣x+3,令x=0,则y=3,故点E(0,3),
①当点P在直线CD的上方时,
过点A作直线k∥CD交y轴于点H,作直线m∥CD交y轴于点M,
∵S△PCE=S△ACE,则直线m与直线CD之间的距离和直线k与直线CD之间的距离为3:2,
则ME=EH,
∵直线k∥CD,设直线k的表达式为y=﹣x+b,将点A的坐标代入上式得:0=3+b,解得b=﹣3,
故点H(0,﹣3),
∵ME=EH=×(3+3)=9,
故点M的坐标为(0,12),
同理可得,直线m的表达式为y=﹣x+12②,
联立①②并解得,
故点P(2,10);
②当点P在直线CD的下方时,
同理可得,点P(﹣4,﹣2);
综上,点P的坐标为(2,10)或(﹣4,﹣2);
(3)存在,理由:
设点Q(m,3﹣m),
由点B、E、Q的坐标得:BQ2=m2+(3﹣m﹣6)2,BE2=9,QE2=2m2,
当BQ=BE时,即m2+(3﹣m﹣6)2=9,解得m=0(舍去)﹣3;
当BQ=EQ时,同理可得:m=﹣;
当BE=QE时,同理可得:m=±;
综上,点Q的坐标为(,3﹣)或(﹣,3+)或(﹣,)或(﹣3,6).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
