2021-2022学年鲁教版(五四制 )七年级数学上册第5章位置与坐标 期末复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制 )七年级数学上册第5章位置与坐标 期末复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 15:03:45 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》期末复习训练(附答案)
1.在平面直角坐标系中,点P(﹣3,4)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
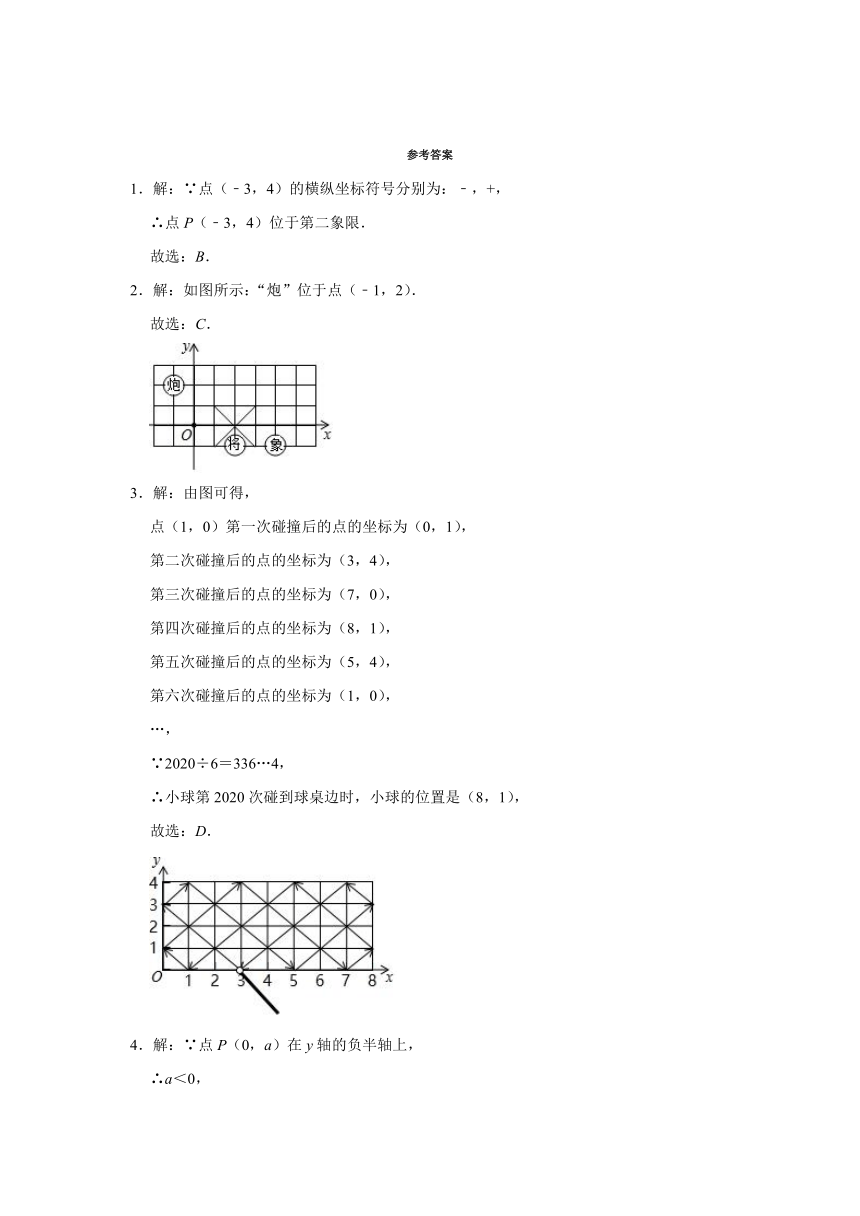
2.如图,象棋盘上“将”位于点(2,﹣1),“象”位于点(4,﹣1),则“炮”位于点( )
A.(1,2) B.(2,﹣1) C.(﹣1,2) D.(2,1)
3.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4) B.(5,4) C.(7,0) D.(8,1)
4.已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点P(x,y)在第四象限,且到y轴的距离为3,到x轴的距离为5,则点P的坐标是( )
A.(3,﹣5) B.(5,﹣3) C.(﹣3,5) D.(﹣5,3)
6.已知点P的坐标是(﹣2﹣,1),则点P在第 象限.
7.如图,在正方形的网格中建立平面直角坐标系,若B、C两点的坐标分别是B(0,2),C(1,0),则A点的坐标为 .
8.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),“兵”的坐标是(﹣2,3),那么“帅”的坐标是 .
9.在平面直角坐标系中,已知点A(2﹣a,2a+3)在第四象限.若点A在两坐标轴夹角平分线上,则a的值为 .
10.已知点M(a﹣3,4﹣a)在y轴上,则点M的坐标为 .
11.已知点A(m﹣1,﹣5)和点B(2,m+1),若直线AB∥x轴,则线段AB的长为 .
12.已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为 .
13.若点A(a+1,3)与点B(﹣2,b+2)关于y轴对称,则a+b= .
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y= .
15.在平面直角坐标系中,点A(1,﹣1)和B(1,1)关于 轴对称.
16.在平面直角坐标系中,点A(m﹣n,2m+n)在第二象限,到x轴和y轴的距离分别为4,1,试求(m﹣n)2021的值.
17.如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.
18.如果点P(m+3,m﹣2)在坐标轴上,求m的值和点p的坐标.
19.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
20.如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格上.
(1)画出△ABC关于y轴对称的图形△A′B′C′,并写出A′,B′,C′的坐标;
(2)若点D在图中所给网格中的格点上,且以A,B,D为顶点的三角形为等腰直角三角形,请直接写出点D的坐标.
参考答案
1.解:∵点(﹣3,4)的横纵坐标符号分别为:﹣,+,
∴点P(﹣3,4)位于第二象限.
故选:B.
2.解:如图所示:“炮”位于点(﹣1,2).
故选:C.
3.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
4.解:∵点P(0,a)在y轴的负半轴上,
∴a<0,
∴﹣a2﹣1<0,﹣a+1>0,
∴点Q在第二象限.
故选:B.
5.解:∵点P(x,y)在第四象限,且到y轴的距离为3,
∴点P的横坐标是3;
∵点P到x轴的距离为5,
∴点P的纵坐标是﹣5,
∴点P的坐标(3,﹣5);
故选:A.
6.解:∵≥0,
∴﹣2﹣<0,
又∵1>0,
∴点P(﹣2﹣,1)在第二象限.
故答案为:二.
7.解:如图所示:A点的坐标为(﹣1,3).
故答案为:(﹣1,3).
8.解:如图所示:“帅”的坐标为(0,﹣1).
故答案为:(0,﹣1).
9.解:∵点A(2﹣a,2a+3)在第四象限,点A在两坐标轴夹角平分线上,
∴2﹣a+2a+3=0,
解得:a=﹣5.
故答案为:﹣5.
10.解:∵点M(a﹣3,4﹣a)在y轴上,
∴a﹣3=0,
解得:a=3,
则4﹣a=4﹣3=1.
则点M的坐标为:(0,1).
故答案为:(0,1).
11.解:∵点A(m﹣1,﹣5)和点B(2,m+1),直线AB∥x轴,
∴m+1=﹣5,
解得m=﹣6.
∴2﹣(﹣6﹣1)=9,
故答案为:9.
12.解:∵平面直角坐标系内的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,
∴|2a+2|=4,
解得:a1=1,a2=﹣3.
当a=1时,点A为(5,4),点B为(3,4),符合题意;
当a=﹣3时,点A为(﹣7,4),点B(3,﹣4),符合题意.
故答案为:1或﹣3.
13.解:∵点A(a+1,3)与点B(﹣2,b+2)关于y轴对称,
∴a+1=2,b+2=3,
解得a=1,b=1,
∴a+b=2,
故答案为:2.
14.解:∵点P(x,y)关于原点的对称点为(2,3),
∴x=﹣2,y=﹣3;
∴x+y=﹣2﹣3=﹣5.
故答案是:﹣5.
15.解:点A(1,﹣1)和B(1,1)关于x轴对称,
故答案为x.
16.解:∵点A(m﹣n,2m+n)在第二象限,到x轴和y轴的距离分别为4,1,
∴,
解得,
所以,(m﹣n)2021=(﹣1)2021=﹣1.
17.解:(1)如图所示:
(2)由平面直角坐标系知,教学楼的坐标为(1,0),体育馆的坐标为(﹣4,3);
(3)行政楼的位置如图所示.
18.解:∵点P(m+3,m﹣2)在坐标轴上,
∴m+3=0或m﹣2=0,
∴m=﹣3或m=2,
∴点P(0,﹣5)或(5,0).
19.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2时,a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12)或(﹣4,4).
20.解:(1)所作图形如图所示:
;
(2)点D的坐标为(2,4)或(2,1)或(﹣4,4)或(﹣4,1).
1.在平面直角坐标系中,点P(﹣3,4)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,象棋盘上“将”位于点(2,﹣1),“象”位于点(4,﹣1),则“炮”位于点( )
A.(1,2) B.(2,﹣1) C.(﹣1,2) D.(2,1)
3.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4) B.(5,4) C.(7,0) D.(8,1)
4.已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点P(x,y)在第四象限,且到y轴的距离为3,到x轴的距离为5,则点P的坐标是( )
A.(3,﹣5) B.(5,﹣3) C.(﹣3,5) D.(﹣5,3)
6.已知点P的坐标是(﹣2﹣,1),则点P在第 象限.
7.如图,在正方形的网格中建立平面直角坐标系,若B、C两点的坐标分别是B(0,2),C(1,0),则A点的坐标为 .
8.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),“兵”的坐标是(﹣2,3),那么“帅”的坐标是 .
9.在平面直角坐标系中,已知点A(2﹣a,2a+3)在第四象限.若点A在两坐标轴夹角平分线上,则a的值为 .
10.已知点M(a﹣3,4﹣a)在y轴上,则点M的坐标为 .
11.已知点A(m﹣1,﹣5)和点B(2,m+1),若直线AB∥x轴,则线段AB的长为 .
12.已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为 .
13.若点A(a+1,3)与点B(﹣2,b+2)关于y轴对称,则a+b= .
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y= .
15.在平面直角坐标系中,点A(1,﹣1)和B(1,1)关于 轴对称.
16.在平面直角坐标系中,点A(m﹣n,2m+n)在第二象限,到x轴和y轴的距离分别为4,1,试求(m﹣n)2021的值.
17.如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.
18.如果点P(m+3,m﹣2)在坐标轴上,求m的值和点p的坐标.
19.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
20.如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格上.
(1)画出△ABC关于y轴对称的图形△A′B′C′,并写出A′,B′,C′的坐标;
(2)若点D在图中所给网格中的格点上,且以A,B,D为顶点的三角形为等腰直角三角形,请直接写出点D的坐标.
参考答案
1.解:∵点(﹣3,4)的横纵坐标符号分别为:﹣,+,
∴点P(﹣3,4)位于第二象限.
故选:B.
2.解:如图所示:“炮”位于点(﹣1,2).
故选:C.
3.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
4.解:∵点P(0,a)在y轴的负半轴上,
∴a<0,
∴﹣a2﹣1<0,﹣a+1>0,
∴点Q在第二象限.
故选:B.
5.解:∵点P(x,y)在第四象限,且到y轴的距离为3,
∴点P的横坐标是3;
∵点P到x轴的距离为5,
∴点P的纵坐标是﹣5,
∴点P的坐标(3,﹣5);
故选:A.
6.解:∵≥0,
∴﹣2﹣<0,
又∵1>0,
∴点P(﹣2﹣,1)在第二象限.
故答案为:二.
7.解:如图所示:A点的坐标为(﹣1,3).
故答案为:(﹣1,3).
8.解:如图所示:“帅”的坐标为(0,﹣1).
故答案为:(0,﹣1).
9.解:∵点A(2﹣a,2a+3)在第四象限,点A在两坐标轴夹角平分线上,
∴2﹣a+2a+3=0,
解得:a=﹣5.
故答案为:﹣5.
10.解:∵点M(a﹣3,4﹣a)在y轴上,
∴a﹣3=0,
解得:a=3,
则4﹣a=4﹣3=1.
则点M的坐标为:(0,1).
故答案为:(0,1).
11.解:∵点A(m﹣1,﹣5)和点B(2,m+1),直线AB∥x轴,
∴m+1=﹣5,
解得m=﹣6.
∴2﹣(﹣6﹣1)=9,
故答案为:9.
12.解:∵平面直角坐标系内的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,
∴|2a+2|=4,
解得:a1=1,a2=﹣3.
当a=1时,点A为(5,4),点B为(3,4),符合题意;
当a=﹣3时,点A为(﹣7,4),点B(3,﹣4),符合题意.
故答案为:1或﹣3.
13.解:∵点A(a+1,3)与点B(﹣2,b+2)关于y轴对称,
∴a+1=2,b+2=3,
解得a=1,b=1,
∴a+b=2,
故答案为:2.
14.解:∵点P(x,y)关于原点的对称点为(2,3),
∴x=﹣2,y=﹣3;
∴x+y=﹣2﹣3=﹣5.
故答案是:﹣5.
15.解:点A(1,﹣1)和B(1,1)关于x轴对称,
故答案为x.
16.解:∵点A(m﹣n,2m+n)在第二象限,到x轴和y轴的距离分别为4,1,
∴,
解得,
所以,(m﹣n)2021=(﹣1)2021=﹣1.
17.解:(1)如图所示:
(2)由平面直角坐标系知,教学楼的坐标为(1,0),体育馆的坐标为(﹣4,3);
(3)行政楼的位置如图所示.
18.解:∵点P(m+3,m﹣2)在坐标轴上,
∴m+3=0或m﹣2=0,
∴m=﹣3或m=2,
∴点P(0,﹣5)或(5,0).
19.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2时,a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12)或(﹣4,4).
20.解:(1)所作图形如图所示:
;
(2)点D的坐标为(2,4)或(2,1)或(﹣4,4)或(﹣4,1).
