2021-2022学年苏科版九年级数学下册期末复习训练: 第7章锐角三角函数(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册期末复习训练: 第7章锐角三角函数(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 19:10:16 | ||
图片预览


文档简介
2021-2022学年苏科版九年级数学下册《第7章锐角三角函数》期末复习训练2(附答案)
1.已知在Rt△ABC中,∠C=90°,BC=5,那么AB的长为( )
A.5sinA B.5cosA C. D.
2.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
3.tan35° cotα=1,则α等于( )
A.65° B.35° C.75° D.55°
4.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A. B. C. D.
5.在△ABC中,∠C=90°,cosA=,那么∠A的度数为( )
A.45° B.60° C.30° D.75°
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,处于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为( )(参考数据:1.4,≈1.7)
A.7米 B.14米 C.20米 D.40米
9.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
10.如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶一上D点处测得条幅顶端A的仰角为36.9°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为63.5°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度约为( )
(参考数据:sin36.9°≈0.60,tan36.9°≈0.75,sin63.5°≈0.89,tan63.5°≈2.00)
A.7米 B.8米 C.9米 D.10米
11.如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°北方向上,那么汽车由B处到达离楼H距离最近的位置C时,需要继续行驶的时间为( )
A.60分钟 B.30分钟 C.15分钟 D.45分钟
12.如果等腰三角形的周长是底边长的5倍,那么它的顶角的正弦值为( )
A. B. C. D.
13.某建筑物的走廊墙壁上搭了一个长4m的梯子,梯子底端正好与地面成45°角,影响了人们的正常行走,为了拓宽行路通道,将梯子挪动位置,使其与地面的倾斜角恰为60°,则行路通道被拓宽了 m(结果保留根号)
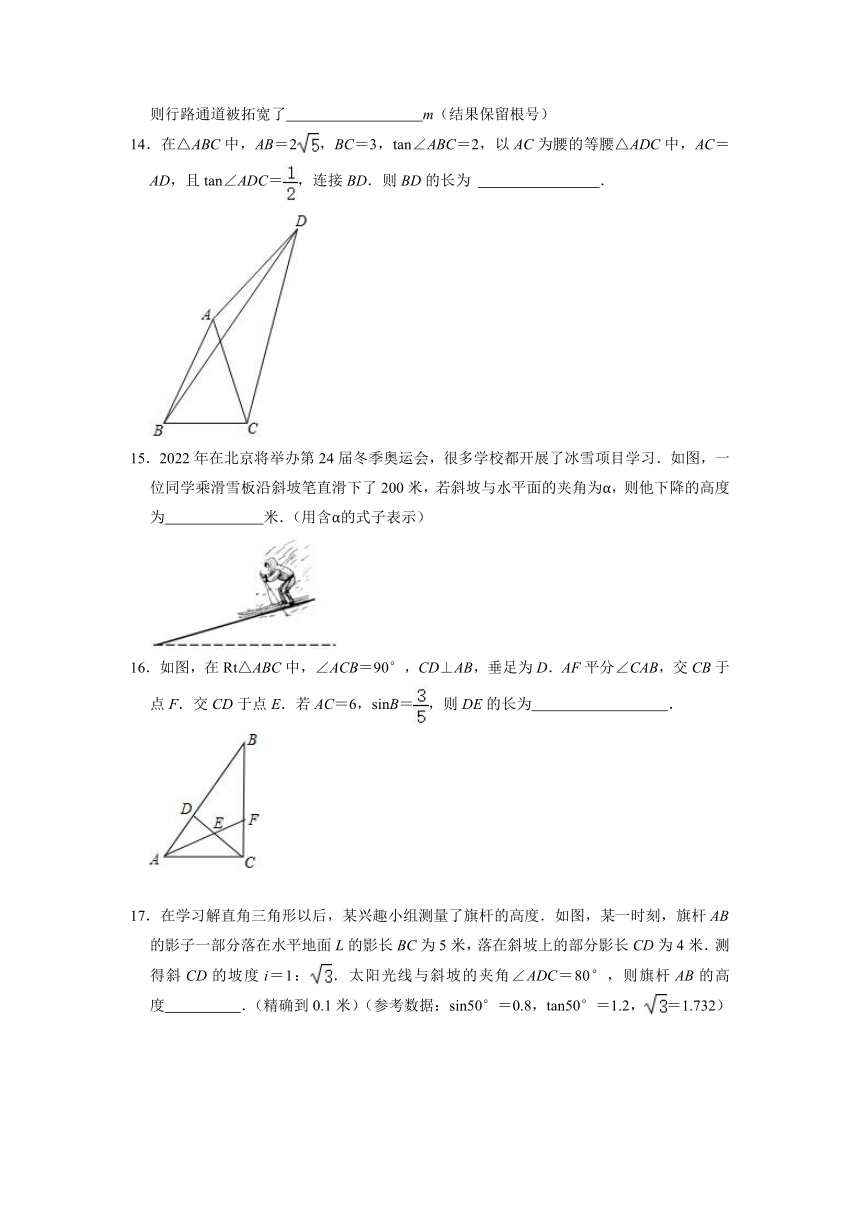
14.在△ABC中,AB=2,BC=3,tan∠ABC=2,以AC为腰的等腰△ADC中,AC=AD,且tan∠ADC=,连接BD.则BD的长为 .
15.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为α,则他下降的高度为 米.(用含α的式子表示)
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
17.在学习解直角三角形以后,某兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在水平地面L的影长BC为5米,落在斜坡上的部分影长CD为4米.测得斜CD的坡度i=1:.太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度 .(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,=1.732)
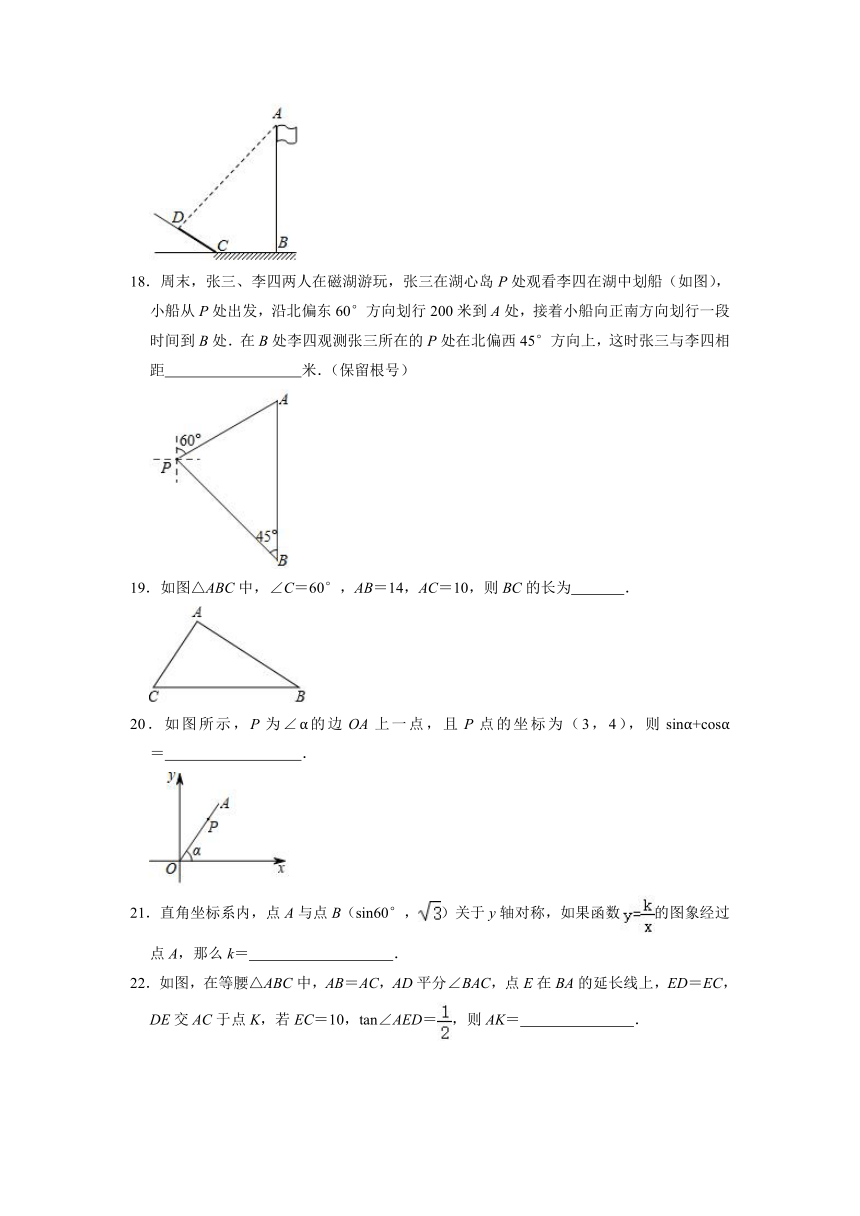
18.周末,张三、李四两人在磁湖游玩,张三在湖心岛P处观看李四在湖中划船(如图),小船从P处出发,沿北偏东60°方向划行200米到A处,接着小船向正南方向划行一段时间到B处.在B处李四观测张三所在的P处在北偏西45°方向上,这时张三与李四相距 米.(保留根号)
19.如图△ABC中,∠C=60°,AB=14,AC=10,则BC的长为 .
20.如图所示,P为∠α的边OA上一点,且P点的坐标为(3,4),则sinα+cosα= .
21.直角坐标系内,点A与点B(sin60°,)关于y轴对称,如果函数的图象经过点A,那么k= .
22.如图,在等腰△ABC中,AB=AC,AD平分∠BAC,点E在BA的延长线上,ED=EC,DE交AC于点K,若EC=10,tan∠AED=,则AK= .
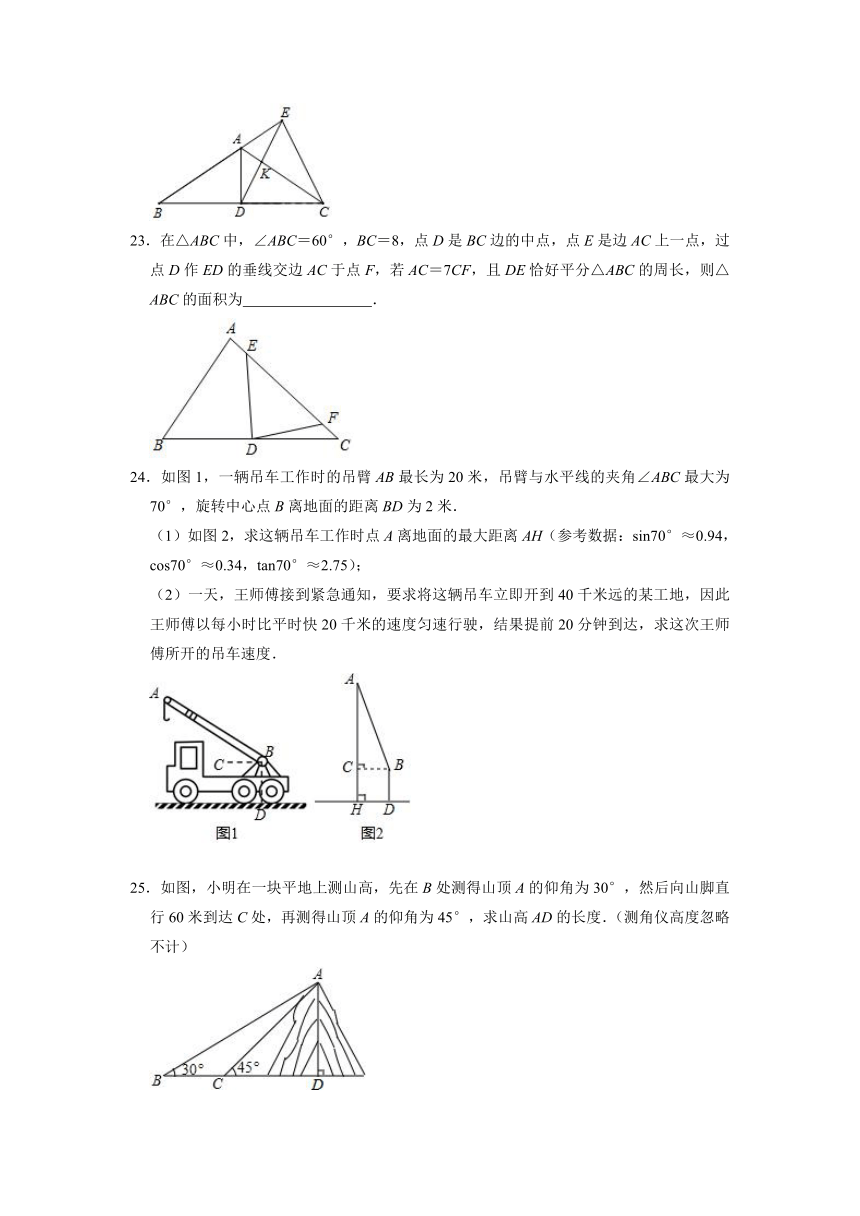
23.在△ABC中,∠ABC=60°,BC=8,点D是BC边的中点,点E是边AC上一点,过点D作ED的垂线交边AC于点F,若AC=7CF,且DE恰好平分△ABC的周长,则△ABC的面积为 .
24.如图1,一辆吊车工作时的吊臂AB最长为20米,吊臂与水平线的夹角∠ABC最大为70°,旋转中心点B离地面的距离BD为2米.
(1)如图2,求这辆吊车工作时点A离地面的最大距离AH(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75);
(2)一天,王师傅接到紧急通知,要求将这辆吊车立即开到40千米远的某工地,因此王师傅以每小时比平时快20千米的速度匀速行驶,结果提前20分钟到达,求这次王师傅所开的吊车速度.
25.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行60米到达C处,再测得山顶A的仰角为45°,求山高AD的长度.(测角仪高度忽略不计)
26.阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2∠A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
27.楼房AB后有一假山,其坡度为i=1:,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
参考答案
1.解:∵Rt△ABC中,∠C=90°,BC=5,
∴sinA==,
∴AB=,
故选:C.
2.解:∵cosA=sin(90°﹣A),余弦函数随角增大而减小,
∴当0°<∠A<45°时,sinA<cosA,即sinA﹣cosA<0.
故选:B.
3.解:由tan35° cotα=1,得α=35°.
故选:B.
4.解:如图所示:∵∠C=90°,cosB=,
∴设BC=3x,则AB=5x,
故AC=4x,
则tanA==.
故选:C.
5.解:∵∠C=90°,cosA=,
∴∠A=60°.
故选:B.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
8.解:如图,作BH⊥AC于H.
∵∠BCH=45°,∠BHC=90°,
∴∠HCB=∠HBC=45°,
∴HC=HB,设HC=BH=xm,
∵∠A=60°,
∴AH=x,
∴x+x=20,
∴x=10(3﹣),
∴AB=2AH=2××10(3﹣)≈14(m)
故选:B.
9.解:在Rt△ABC中,∵∠ABC=90°,AB=2米,
∴sinα=,
∴0.8=,
∴AC=2.5米,BC==1.5米,
在Rt△ECD中,∵∠EDC=90°,ED=2.4米,EC=AC=2.5米,
∴CD==0.7,
∴BD=CD+BC=0.7+1.5=2.2米,
故选:C.
10.解:作DF⊥AB于点F,如右图所示,
由题意可得,DF=CB,
∵台阶DE的坡度为1:2,DC=2米,
∴CE=2CD=4米,
∵∠AFD=90°,∠ADF=36.9°,DC=2米,tan∠ADF=,
∴tan36.9°=,
即DF=,
又∵∠ABE=90°,∠AEB=63.5°,CE=4米,CB=DF,tan∠AEB=,
∴BE=,
即DF﹣4=,
∴,
解得,AB≈8米,
故选:B.
11.解:作HC⊥AB交AB的延长线于C,
由题意得,∠HAB=60°,∠ABH=120°,
∴∠AHB=30°,
∴BA=BH,
∵∠ABH=120°,
∴∠CBH=60°,又HC⊥AB,
∴∠BHC=30°,
∴BC=BH,
∴BC=AB,
∵从A到B行驶了1个小时,
∴该车继续行驶30分钟可使汽车到达离楼H距离最近的位置,
故选:B.
12.解:∵等腰三角形的周长是底边长的5倍,设底边为a,则腰长为2a.
作AD⊥BC于D点,CE⊥AB于E点.
∴AB=AC=2a,BD=a,
在Rt△ABD中,AD==,
∵S△ABC=BC AD=AB CE,
∴CE=.
∴sin∠BAC==.
故选:A.
13.解:∵AB=CD=4,∠B=45°,∠CDO=60°,
∴OB=AB cos45°=2(米);
OD=CD cos60°=AB sin30°=2(米).
则BD=OB﹣OD=2﹣2(米).
所以拓宽了行路通道2﹣2(米).
故答案为:2﹣2
14.解:作AE⊥BC于E,AH⊥CD于H,作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∵AB=2,tan∠ABC=2,
∴tan∠ABC==2,
∴AE=2BE,
∵AB2=AE2+BE2,即(2)2=5BE2,
∴BE=2,
∴AE=4,EC=BC﹣BE=3﹣2=1,
∴AC==,
∵AC=AD,
∴AD=,DH=HC=DC,
∵tan∠ADC=,
∴tan∠ADC==,
∴DH=2AH,
∵AD2=AH2+DH2,即17=5AH2,
∴AH=,
∴DC=4AH=,
作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∴△PAB∽△DBC;
∴
∴,
∴PA=,
∵tan∠ABC=2,tan∠ADC=,
∴∠ABC+∠ADC=90°,
∴∠BCD+∠BAD=270°,,
∴∠PAD=360°﹣270°=90°,
∴PD==,
∵∠PAB=∠DCB,
∴∠PAD=∠ABC,
∴,
∴△PBD∽△ABC,
∴;
∴,
∴BD=
15.解:如图,设下滑的距离为AB=200米,下降的高度为线段AC.
在Rt△ABC中,AC=AB sinα=200 sinα(米),
故答案为200 sinα.
16.解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
解法二:如图,过点E作EG⊥AC于G.设EC=x.
则EG=DE=x,
∴CD=x+x=,
∴x=3,
∴DE=.
17.解:延长AD交BC的延长线于点E,作DF⊥CE于点F.
在△DCF中,∵CD=4m,DF:CF=1:,
∴tan∠DCF=,
∴∠DCF=30°,∠CDF=60°.
∴DF=2(m),CF=2(m),
在Rt△DEF中,因为∠DEF=50°,
所以EF=≈1.67(m)
∴BE=EF+FC+CB=1.67+2+5≈10.13(m),
∴AB=BE tan50°≈12.2(m),
故答案为12.2m.
18.解:作PD⊥AB于点D,
由已知得PA=200米,∠APD=30°,∠B=45°,
在Rt△PAD中,
由cos30°=,得PD=PAcos30°=200×=100米,
在Rt△PBD中,
由sin45°=,得PB===100(米).
故答案为:100.
19.解:过A作AD⊥BC于D,则∠ADC=∠ADB=90°,
∵∠C=60°,
∴∠CAD=30°,
∴CD=AC==5,
由勾股定理得:AD===5,BD===11,
∴BC=BD+CD=11+5=16,
故答案为:16.
20.解:∵P是∠α的边OA上一点,且P点坐标为(3,4),
∴PB=4,OB=3,OP===5.
故sinα==,cosα==,
∴sinα+cosα=,
故答案为:.
21.解:∵sin60°=,
∴点B(,).
根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”可知:
点A为(﹣,),
∵函数的图象经过点A,
∴k=×=.
22.解:过点K作KM⊥EC,过D作DN∥AC,设KM=m,∠BED=∠α
∵ED=EC=10,
∴∠ECD=∠EDC=∠B+∠α,
∵AB=AC,
∴∠ACB=∠B,
∴∠ECA=∠AED,
∵tanα=,
∴CM=2m,KC=m,
∵DN∥AC,D是BC的中点,
∴ND=AC,∠EAC=∠END,EC=ED,
∴△EAC≌△DNE(AAS),
∴AE=ND,
∵AD⊥BC,AB=AC,
∴ND=AB=AN=BN,
∴4AK=AC,
∵AC=AK+CK,
∴AK=CK=,
∴K是ED的中点,
∴EK=5,
在Rt△EKM中,EM=10﹣2m,KM=m,
∴52=m2+(10﹣2m)2,
∴m=3或m=5(舍)
∴AK=;
故答案为;
23.解:如图,取AC的中点M,连接DM,作AH⊥BC于H.设DM=a,AE=b.
∵BD=DC,AM=MC,
∴AB=2DM=2a,
∵AB+AE+BD=EC+DC,
∴EC=2a+b,AC=2a+2b,
∴AM=MC=a+b,
∴EM=a,
∴EM=DM,
∴∠MED=∠MDE,
∵∠MED+∠MFD=90°,∠MDE+∠MDF=90°,
∴∠MFD=∠MDF,
∴MD=MF=a,
∴CF=AE=b,
∵AC=7CF,
∴2a+2b=7b,
∴2a=5b,
∵AB=5b,AC=7b,
在Rt△ABH中,∵∠B=60°,
∴BH=AB=b,AH=b,
在Rt△ACH中,CH==b,
∴BC=BH+HC=8b,
∴8b=8,
∴b=1,
∴S△ABC=×8×=10,
故答案为10.
24.解:(1)根据题意,得AB=20,∠ABC=70°,CH=BD=2,
在Rt△ACB中,∵∠ACB=90°,
∴AC=AB sin70°=20×0.94=18.8,
∴AH=20.8.
答:这辆吊车工作时点A离地面的最大距离AH为20.8米;
(2)设这次王师傅所开的吊车的速度为每小时x千米,由题意,得
,
解得,x1=60,x2=﹣40,
经检验:x1=60,x2=﹣40都是原方程的解,但x2=﹣40符合题意,舍去,
答:这次王师傅所开的吊车的速度为每小时60千米.
25.解:由题意得,∠ABD=30°,∠ACD=45°,BC=60m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=,
∴CD=AD=x,
∴BD=BC+CD=x+60,
在Rt△ABD中,∵tan∠ABD=,
∴x=(x+60),
∴x=30(+1)米,
答:山高AD为30(+1)米.
26.解:(1)如图3中,在Rt△ABC中,∵AB=3,BC=1,∠C=90°,
∴AC==2,
∴sinA==,cosA=,
∴sin2A=2cosA sinA=
(2)如图2中,cos2A=cos∠CED===2AC cosA﹣1=2(cosA)2﹣1.
27.解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i===tan∠ECF,
∴∠ECF=30°,
∴EF=CE=9米,CF=9米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9)米,
∴AB=AH+HB=(39+9)米.
答:楼房AB的高为(39+9)米.
1.已知在Rt△ABC中,∠C=90°,BC=5,那么AB的长为( )
A.5sinA B.5cosA C. D.
2.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
3.tan35° cotα=1,则α等于( )
A.65° B.35° C.75° D.55°
4.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A. B. C. D.
5.在△ABC中,∠C=90°,cosA=,那么∠A的度数为( )
A.45° B.60° C.30° D.75°
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,处于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为( )(参考数据:1.4,≈1.7)
A.7米 B.14米 C.20米 D.40米
9.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
10.如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶一上D点处测得条幅顶端A的仰角为36.9°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为63.5°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度约为( )
(参考数据:sin36.9°≈0.60,tan36.9°≈0.75,sin63.5°≈0.89,tan63.5°≈2.00)
A.7米 B.8米 C.9米 D.10米
11.如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°北方向上,那么汽车由B处到达离楼H距离最近的位置C时,需要继续行驶的时间为( )
A.60分钟 B.30分钟 C.15分钟 D.45分钟
12.如果等腰三角形的周长是底边长的5倍,那么它的顶角的正弦值为( )
A. B. C. D.
13.某建筑物的走廊墙壁上搭了一个长4m的梯子,梯子底端正好与地面成45°角,影响了人们的正常行走,为了拓宽行路通道,将梯子挪动位置,使其与地面的倾斜角恰为60°,则行路通道被拓宽了 m(结果保留根号)
14.在△ABC中,AB=2,BC=3,tan∠ABC=2,以AC为腰的等腰△ADC中,AC=AD,且tan∠ADC=,连接BD.则BD的长为 .
15.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为α,则他下降的高度为 米.(用含α的式子表示)
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
17.在学习解直角三角形以后,某兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在水平地面L的影长BC为5米,落在斜坡上的部分影长CD为4米.测得斜CD的坡度i=1:.太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度 .(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,=1.732)
18.周末,张三、李四两人在磁湖游玩,张三在湖心岛P处观看李四在湖中划船(如图),小船从P处出发,沿北偏东60°方向划行200米到A处,接着小船向正南方向划行一段时间到B处.在B处李四观测张三所在的P处在北偏西45°方向上,这时张三与李四相距 米.(保留根号)
19.如图△ABC中,∠C=60°,AB=14,AC=10,则BC的长为 .
20.如图所示,P为∠α的边OA上一点,且P点的坐标为(3,4),则sinα+cosα= .
21.直角坐标系内,点A与点B(sin60°,)关于y轴对称,如果函数的图象经过点A,那么k= .
22.如图,在等腰△ABC中,AB=AC,AD平分∠BAC,点E在BA的延长线上,ED=EC,DE交AC于点K,若EC=10,tan∠AED=,则AK= .
23.在△ABC中,∠ABC=60°,BC=8,点D是BC边的中点,点E是边AC上一点,过点D作ED的垂线交边AC于点F,若AC=7CF,且DE恰好平分△ABC的周长,则△ABC的面积为 .
24.如图1,一辆吊车工作时的吊臂AB最长为20米,吊臂与水平线的夹角∠ABC最大为70°,旋转中心点B离地面的距离BD为2米.
(1)如图2,求这辆吊车工作时点A离地面的最大距离AH(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75);
(2)一天,王师傅接到紧急通知,要求将这辆吊车立即开到40千米远的某工地,因此王师傅以每小时比平时快20千米的速度匀速行驶,结果提前20分钟到达,求这次王师傅所开的吊车速度.
25.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行60米到达C处,再测得山顶A的仰角为45°,求山高AD的长度.(测角仪高度忽略不计)
26.阅读下列材料:
题目:如图1,在△ABC中,已知∠A(∠A<45°),∠C=90°,AB=1,请用sinA、cosA表示sin2A.
解:如图2,作AB边上的中线CE,CD⊥AB于D,
则CE=AB=,∠CED=2∠A,CD=ACsinA,AC=ABcosA=cosA
在Rt△CED中,sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读,请解决下列问题:
(1)如图3,在△ABC中,∠C=90°,BC=1,AB=3,求sinA,sin2A的值;
(2)上面阅读材料中,题目条件不变,请用sinA或cosA表示cos2A.
27.楼房AB后有一假山,其坡度为i=1:,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
参考答案
1.解:∵Rt△ABC中,∠C=90°,BC=5,
∴sinA==,
∴AB=,
故选:C.
2.解:∵cosA=sin(90°﹣A),余弦函数随角增大而减小,
∴当0°<∠A<45°时,sinA<cosA,即sinA﹣cosA<0.
故选:B.
3.解:由tan35° cotα=1,得α=35°.
故选:B.
4.解:如图所示:∵∠C=90°,cosB=,
∴设BC=3x,则AB=5x,
故AC=4x,
则tanA==.
故选:C.
5.解:∵∠C=90°,cosA=,
∴∠A=60°.
故选:B.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
8.解:如图,作BH⊥AC于H.
∵∠BCH=45°,∠BHC=90°,
∴∠HCB=∠HBC=45°,
∴HC=HB,设HC=BH=xm,
∵∠A=60°,
∴AH=x,
∴x+x=20,
∴x=10(3﹣),
∴AB=2AH=2××10(3﹣)≈14(m)
故选:B.
9.解:在Rt△ABC中,∵∠ABC=90°,AB=2米,
∴sinα=,
∴0.8=,
∴AC=2.5米,BC==1.5米,
在Rt△ECD中,∵∠EDC=90°,ED=2.4米,EC=AC=2.5米,
∴CD==0.7,
∴BD=CD+BC=0.7+1.5=2.2米,
故选:C.
10.解:作DF⊥AB于点F,如右图所示,
由题意可得,DF=CB,
∵台阶DE的坡度为1:2,DC=2米,
∴CE=2CD=4米,
∵∠AFD=90°,∠ADF=36.9°,DC=2米,tan∠ADF=,
∴tan36.9°=,
即DF=,
又∵∠ABE=90°,∠AEB=63.5°,CE=4米,CB=DF,tan∠AEB=,
∴BE=,
即DF﹣4=,
∴,
解得,AB≈8米,
故选:B.
11.解:作HC⊥AB交AB的延长线于C,
由题意得,∠HAB=60°,∠ABH=120°,
∴∠AHB=30°,
∴BA=BH,
∵∠ABH=120°,
∴∠CBH=60°,又HC⊥AB,
∴∠BHC=30°,
∴BC=BH,
∴BC=AB,
∵从A到B行驶了1个小时,
∴该车继续行驶30分钟可使汽车到达离楼H距离最近的位置,
故选:B.
12.解:∵等腰三角形的周长是底边长的5倍,设底边为a,则腰长为2a.
作AD⊥BC于D点,CE⊥AB于E点.
∴AB=AC=2a,BD=a,
在Rt△ABD中,AD==,
∵S△ABC=BC AD=AB CE,
∴CE=.
∴sin∠BAC==.
故选:A.
13.解:∵AB=CD=4,∠B=45°,∠CDO=60°,
∴OB=AB cos45°=2(米);
OD=CD cos60°=AB sin30°=2(米).
则BD=OB﹣OD=2﹣2(米).
所以拓宽了行路通道2﹣2(米).
故答案为:2﹣2
14.解:作AE⊥BC于E,AH⊥CD于H,作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∵AB=2,tan∠ABC=2,
∴tan∠ABC==2,
∴AE=2BE,
∵AB2=AE2+BE2,即(2)2=5BE2,
∴BE=2,
∴AE=4,EC=BC﹣BE=3﹣2=1,
∴AC==,
∵AC=AD,
∴AD=,DH=HC=DC,
∵tan∠ADC=,
∴tan∠ADC==,
∴DH=2AH,
∵AD2=AH2+DH2,即17=5AH2,
∴AH=,
∴DC=4AH=,
作∠PAB=∠DCB,∠PBA=∠DBC,PG⊥BD,
∴△PAB∽△DBC;
∴
∴,
∴PA=,
∵tan∠ABC=2,tan∠ADC=,
∴∠ABC+∠ADC=90°,
∴∠BCD+∠BAD=270°,,
∴∠PAD=360°﹣270°=90°,
∴PD==,
∵∠PAB=∠DCB,
∴∠PAD=∠ABC,
∴,
∴△PBD∽△ABC,
∴;
∴,
∴BD=
15.解:如图,设下滑的距离为AB=200米,下降的高度为线段AC.
在Rt△ABC中,AC=AB sinα=200 sinα(米),
故答案为200 sinα.
16.解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
解法二:如图,过点E作EG⊥AC于G.设EC=x.
则EG=DE=x,
∴CD=x+x=,
∴x=3,
∴DE=.
17.解:延长AD交BC的延长线于点E,作DF⊥CE于点F.
在△DCF中,∵CD=4m,DF:CF=1:,
∴tan∠DCF=,
∴∠DCF=30°,∠CDF=60°.
∴DF=2(m),CF=2(m),
在Rt△DEF中,因为∠DEF=50°,
所以EF=≈1.67(m)
∴BE=EF+FC+CB=1.67+2+5≈10.13(m),
∴AB=BE tan50°≈12.2(m),
故答案为12.2m.
18.解:作PD⊥AB于点D,
由已知得PA=200米,∠APD=30°,∠B=45°,
在Rt△PAD中,
由cos30°=,得PD=PAcos30°=200×=100米,
在Rt△PBD中,
由sin45°=,得PB===100(米).
故答案为:100.
19.解:过A作AD⊥BC于D,则∠ADC=∠ADB=90°,
∵∠C=60°,
∴∠CAD=30°,
∴CD=AC==5,
由勾股定理得:AD===5,BD===11,
∴BC=BD+CD=11+5=16,
故答案为:16.
20.解:∵P是∠α的边OA上一点,且P点坐标为(3,4),
∴PB=4,OB=3,OP===5.
故sinα==,cosα==,
∴sinα+cosα=,
故答案为:.
21.解:∵sin60°=,
∴点B(,).
根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”可知:
点A为(﹣,),
∵函数的图象经过点A,
∴k=×=.
22.解:过点K作KM⊥EC,过D作DN∥AC,设KM=m,∠BED=∠α
∵ED=EC=10,
∴∠ECD=∠EDC=∠B+∠α,
∵AB=AC,
∴∠ACB=∠B,
∴∠ECA=∠AED,
∵tanα=,
∴CM=2m,KC=m,
∵DN∥AC,D是BC的中点,
∴ND=AC,∠EAC=∠END,EC=ED,
∴△EAC≌△DNE(AAS),
∴AE=ND,
∵AD⊥BC,AB=AC,
∴ND=AB=AN=BN,
∴4AK=AC,
∵AC=AK+CK,
∴AK=CK=,
∴K是ED的中点,
∴EK=5,
在Rt△EKM中,EM=10﹣2m,KM=m,
∴52=m2+(10﹣2m)2,
∴m=3或m=5(舍)
∴AK=;
故答案为;
23.解:如图,取AC的中点M,连接DM,作AH⊥BC于H.设DM=a,AE=b.
∵BD=DC,AM=MC,
∴AB=2DM=2a,
∵AB+AE+BD=EC+DC,
∴EC=2a+b,AC=2a+2b,
∴AM=MC=a+b,
∴EM=a,
∴EM=DM,
∴∠MED=∠MDE,
∵∠MED+∠MFD=90°,∠MDE+∠MDF=90°,
∴∠MFD=∠MDF,
∴MD=MF=a,
∴CF=AE=b,
∵AC=7CF,
∴2a+2b=7b,
∴2a=5b,
∵AB=5b,AC=7b,
在Rt△ABH中,∵∠B=60°,
∴BH=AB=b,AH=b,
在Rt△ACH中,CH==b,
∴BC=BH+HC=8b,
∴8b=8,
∴b=1,
∴S△ABC=×8×=10,
故答案为10.
24.解:(1)根据题意,得AB=20,∠ABC=70°,CH=BD=2,
在Rt△ACB中,∵∠ACB=90°,
∴AC=AB sin70°=20×0.94=18.8,
∴AH=20.8.
答:这辆吊车工作时点A离地面的最大距离AH为20.8米;
(2)设这次王师傅所开的吊车的速度为每小时x千米,由题意,得
,
解得,x1=60,x2=﹣40,
经检验:x1=60,x2=﹣40都是原方程的解,但x2=﹣40符合题意,舍去,
答:这次王师傅所开的吊车的速度为每小时60千米.
25.解:由题意得,∠ABD=30°,∠ACD=45°,BC=60m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=,
∴CD=AD=x,
∴BD=BC+CD=x+60,
在Rt△ABD中,∵tan∠ABD=,
∴x=(x+60),
∴x=30(+1)米,
答:山高AD为30(+1)米.
26.解:(1)如图3中,在Rt△ABC中,∵AB=3,BC=1,∠C=90°,
∴AC==2,
∴sinA==,cosA=,
∴sin2A=2cosA sinA=
(2)如图2中,cos2A=cos∠CED===2AC cosA﹣1=2(cosA)2﹣1.
27.解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i===tan∠ECF,
∴∠ECF=30°,
∴EF=CE=9米,CF=9米,
∴BH=EF=9米,HE=BF=BC+CF=(30+9)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(30+9)米,
∴AB=AH+HB=(39+9)米.
答:楼房AB的高为(39+9)米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
