福建省南平市延平区高级中学2022届高三上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 福建省南平市延平区高级中学2022届高三上学期12月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 11:54:43 | ||
图片预览




文档简介
南平市延平区高级中学2022届高三上学期12月月考
数学试卷
满分150分 考试时间120分钟
第Ⅰ卷(选择题,共60分)
1、选择题:本题共8小题,每小题5分,共40分。 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数对应的点的坐标是,则的复数为( )
A. B. C. D.
2.在等差数列中,若,则此数列前30项和等于( )
A.810 B.840 C.870 D.900
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数的零点所在的区间为( )
A.(-1,0) B.(0,) C.(,1) D.(1,2)
5.若正四棱柱ABCD A1B1C1D1的体积为,AB=1,则直线AB1与CD1所成的角为( )
A.30° B.45°
C.60° D.90°
6.函数f(x)=(3x-x3)sinx的部分图象大致为( )
7.在△ABC中,角A,B,C的对边分别为a,b,c.根据下列条件解三角形,其中有两解的是( )
A.A=30°,B=45°,c=5 B.a=4,b=5,C=60°
C.a=8,,B=45° D.a=6,b=8,A=30°
8.函数在内有极值,则实数的取值范围是( )
A. B. C. D.
2、选择题:本题共4小题,每小题5分,共20分。 在每小题给出的四个选项中,有多项是符合题
9.若,则下列结论中正确的是( )
A. B. C. D.
10.已知函数,下列说法正确的有( )
A.函数的周期为 B.
C.在区间上单调递增 D.的图象关于点中心对称
11.正方体ABCD-A1B1C1D1的棱长为1,点E为BA1的中点,下列判断正确的是( )
A.AB平面A1CD B.直线EC1与直线AD是异面直线
C.在直线A1C1上存在点F,使EF⊥平面A1CD D.直线BA1与平面A1CD所成角是
12.在一个数列中,如果,都有(为常数),那么这个数列叫做等积数列,叫做这个数列的公积.已知数列是等积数列,且,,公积为,则( )
A. B. C. D.
3、填空题:本题共4小题,每小题5分,共20分。
13.已知=5,则tan α=_____________.
14.在中,,,,为的三等分点,则____________.
15.已知函数是奇函数.若,求的取值范围_________
16.在四面体PABC中,平面平面ABC,,,则该四面体的外接球的体积为___________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.在①,②,③这三个条件中任选一个,补充在下面问题中,并解答.
已知在中,角A,B,C所对的边分别是a,b,c,___________.
(1)求角A; (2)若,,求的面积.
注:如果选择多个条件分别解答,按第一个解答计分.
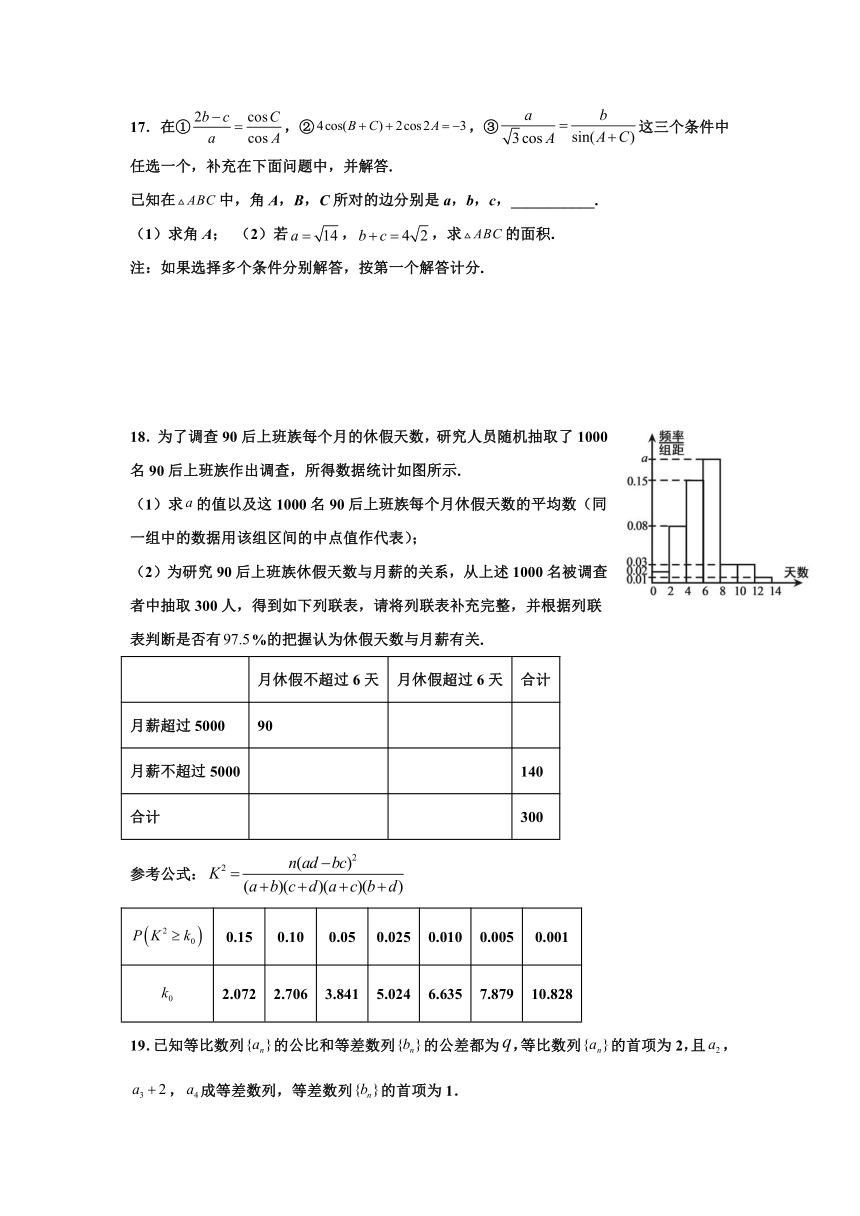
18.为了调查90后上班族每个月的休假天数,研究人员随机抽取了1000名90后上班族作出调查,所得数据统计如图所示.
(1)求的值以及这1000名90后上班族每个月休假天数的平均数(同一组中的数据用该组区间的中点值作代表);
(2)为研究90后上班族休假天数与月薪的关系,从上述1000名被调查者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有%的把握认为休假天数与月薪有关.
月休假不超过6天 月休假超过6天 合计
月薪超过5000 90
月薪不超过5000 140
合计 300
参考公式:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.已知等比数列的公比和等差数列的公差都为,等比数列的首项为2,且,,成等差数列,等差数列的首项为1.
(1)求和的通项公式;
(2)若数列的前项和为,求.
20.在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(1)求证:AB∥平面DEG;
(2)求二面角C DF E的余弦值.
21.全国高中数学联赛活动旨在通过竞赛的方式,培养中学生对于数学的兴趣,让学生喜爱数学,学习数学,激发学生的钻研精神,独立思考精神以及合作精神.现有同学甲、乙二人积极准备参加数学竞赛选拔,在5次模拟训练中,这两位同学的成绩如下表,假设甲、乙二人每次训练成绩相互独立.
第1次 第2次 第3次 第4次 第5次
甲 86 92 87 89 86
乙 90 86 89 88 87
(1)从5次训练中随机选取1次,求甲的成绩高于乙的成绩的概率;
(2)从5次训练中随机选取2次,用表示甲的成绩高于乙的成绩的次数,求的分布列和数学期望;
(3)根据数据信息,你认为谁在选拔中更具竞争力,并说明理由.
(注:样本数据的方差,其中)
22.已知函数在点处的切线平行于x轴.
(1)求实数a,b的值;
(2)讨论函数的零点个数.
参考答案
1.D【详解】由题知,,则,所以,
故选:D.
2.B【详解】
设此数列前30项和为,则,
故选:B.
3.B【详解】求解二次不等式可得:,
∵ 由可推出,由不能推出,
∴ 是的必要不充分条件.
故选:B.
4.C
【详解】
由题设,,,,,
∴零点所在的区间为(,1).
故选:C
5.C
6.A
7.D【详解】对于选项A中:由A=30°,B=45°,c=5,所以,再利用正弦定理可求,显然只有一解;
对于选项B中:由余弦定理可得,所以只有一解;
对于选项C中:因为,且,所以只有一解;
对于选项D中:因为,且,所以角有两解.
故选:D.
8.C
【详解】由得,,
因函数在内有极值,则时,有解,
即在时,函数与直线y=a有公共点,
而,即在上单调递减,,则,显然在零点左右两侧异号,
所以实数的取值范围是.
故选:C
9.ABD
【详解】
由题知,
所以,
对于A选项,由于在上单调递减,
所以当时,可以得到,故A正确,
对于B选项,因为,不等式两边同乘负数得,
故B正确,
对于C选项,因为,所以,
故C错误,
对于D选项,由于在上单调递增,
所以当时,可以得到,故D正确,
故选:ABD.
10.BC
【详解】
A:,,显然,故的周期为错误;
B:,正确;
C:在上,,易知在区间上递增,正确;
D:,,显然,故关于点中心对称错误;
故选:BC
11.ACD
【详解】
对于选项A,结合正方体的性质,可知,故易得AB平面A1CD,故A正确;
对于选项B, 结合正方体的性质,易知直线与直线都在平面中,故B错误;
对于选项C,取的中点,连接、、、 ,易知,
结合正方体的性质,易知平面,故平面,
即在点处时,平面,故C正确;
对于选项D,取的中点,结合正方体的性质,易知平面,
因此即为直线与平面所成角,
因为 ,,所以,故D正确.
故选:ACD.
12.B
【详解】
由题意可知,则对任意的,,则,,
由,得,,,
,因此,.
故选:B.
13.2
14.
【详解】
设,,
同理,,
由得:,
∴
.
故答案为:.
15.
16.
【详解】
解析:如图,设AB的中点为D,连接PD,DC,因为,,所以,,
又平面平面ABC,所以平面ABC,平面PAB.
设该四面体外接球的球心为O,,的外接圆圆心分别为,,
易知,分别在直线DC,PD上,连接,,则平面ABC,所以,则四边形为矩形.
设,的外接圆半径分别为,,外接球的半径为R,
在中,由正弦定理得,则.
在中,,易得,所以,
所以,得,则,连接PO,
在中,,
所以该四面体的外接球的体积.
故答案为:.
17.
(1)
(2)
(1)方案一:选条件①.
根据正弦定理及得,
整理得,
即,
易知,
所以,
又,所以,
又,(注意角的范围)故.
方案二:选条件②.
在中,,所以,
结合二倍角公式,可得,
所以,
得.
又,所以.
方案三:选条件③.
在中,,所以,
所以,
结合正弦定理可得,,得.
又,所以.
(2)
根据余弦定理可得,
,
又,,,
所以,得,
所以.
18.
(1),这1000名90后上班族每个月休假天数的平均数为6
(2)有%的把握认为休假天数与月薪有关,理由见解析
(1)
因为,所以
这1000名90后上班族每个月休假天数的平均数为
(2)
1000名中月休假不超过6天的总人数为人,
超过6天的总人数为500人,
按分层抽样可得这300人中不超过6天的人数为150人,超过6天的人数为150人
所以
月休假不超过6天 月休假超过6天 合计
月薪超过5000 90 70 160
月薪不超过5000 60 80 140
合计 150 150 300
所以有%的把握认为休假天数与月薪有关.
19.
(1),
(2)
(1)
因为,,成等差数列,所以:,整理得:,
即,故,解得,
所以,.
(2)
证明:(2)由(1)得:,
故①,
②,
①②得:,故.
20.【解】 (1)证明:因为AD∥EF,EF∥BC,
所以AD∥BC,又BC=2AD,G是BC的中点,
所以AD//BG且AD=BG,所以四边形ADGB是平行四边形,所以AB∥DG.
因为AB 平面DEG,DG 平面DEG,
所以AB∥平面DEG.
(2)因为EF⊥平面AEB,AE 平面AEB,BE 平面AEB,
所以EF⊥AE,EF⊥BE,又AE⊥EB,
所以EB,EF,EA两两垂直.
以点E为坐标原点,EB,EF,EA所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系.
则E(0,0,0),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2).
由已知得=(2,0,0)是平面EFDA的一个法向量.
设平面DCF的法向量为n=(x,y,z),
则因为=(0,-1,2),=(2,1,0),所以令z=1,得y=2,x=-1,所以可取n=(-1,2,1).
设二面角C DF E的大小为θ,则cos θ=cos〈n,〉==-.
易知二面角C DF E为钝二面角,
所以二面角C DF E的余弦值为-.
21.
(1);
(2)分布列见解析,数学期望为;
(3)乙在选拔中更具竞争力,理由见解析.
(1)
在5次模拟训练中,甲的成绩高于乙的成绩有2次,乙的成绩高于甲的成绩有3次,
从5次训练中随机选取1次的试验有5个基本事件,它们等可能,甲的成绩高于乙的成绩的事件A有2个基本事件,
所以甲的成绩高于乙的成绩的概率.
(2)
的所有可能值是:0,1,2,
,,,
所以的分布列为:
0 1 2
数学期望为.
(3)
甲的平均成绩为,
乙的平均成绩为,
甲成绩的方差,
乙成绩的方差,
虽然,但,因此得乙的成绩更稳定,
所以乙在选拔中更具竞争力.
22.
(1)
(2)函数在上有两个零点.
(1)
因为,所以,
由题意可知,解得,
(2)
由(1)知,所以,
由于,所以当时,,所以在上单调递增,因为时,,而,因此时,,因此函数在上无零点;
则,当时,,则在上单调递减,且,因为,则,由零点存在性知在上存在唯一零点;
当时 ,令,则,所以在上单调递增,且,,由零点存在性定理知存在唯一零点,使得,因此在时单调递减,在时单调递增,且,,,由零点存在性定理知存在唯一零点在上,因此在上存在唯一零点;
当时,,则在上单调递增,且,所以在上无零点;
综上所述:函数在上有两个零点.
数学试卷
满分150分 考试时间120分钟
第Ⅰ卷(选择题,共60分)
1、选择题:本题共8小题,每小题5分,共40分。 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数对应的点的坐标是,则的复数为( )
A. B. C. D.
2.在等差数列中,若,则此数列前30项和等于( )
A.810 B.840 C.870 D.900
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数的零点所在的区间为( )
A.(-1,0) B.(0,) C.(,1) D.(1,2)
5.若正四棱柱ABCD A1B1C1D1的体积为,AB=1,则直线AB1与CD1所成的角为( )
A.30° B.45°
C.60° D.90°
6.函数f(x)=(3x-x3)sinx的部分图象大致为( )
7.在△ABC中,角A,B,C的对边分别为a,b,c.根据下列条件解三角形,其中有两解的是( )
A.A=30°,B=45°,c=5 B.a=4,b=5,C=60°
C.a=8,,B=45° D.a=6,b=8,A=30°
8.函数在内有极值,则实数的取值范围是( )
A. B. C. D.
2、选择题:本题共4小题,每小题5分,共20分。 在每小题给出的四个选项中,有多项是符合题
9.若,则下列结论中正确的是( )
A. B. C. D.
10.已知函数,下列说法正确的有( )
A.函数的周期为 B.
C.在区间上单调递增 D.的图象关于点中心对称
11.正方体ABCD-A1B1C1D1的棱长为1,点E为BA1的中点,下列判断正确的是( )
A.AB平面A1CD B.直线EC1与直线AD是异面直线
C.在直线A1C1上存在点F,使EF⊥平面A1CD D.直线BA1与平面A1CD所成角是
12.在一个数列中,如果,都有(为常数),那么这个数列叫做等积数列,叫做这个数列的公积.已知数列是等积数列,且,,公积为,则( )
A. B. C. D.
3、填空题:本题共4小题,每小题5分,共20分。
13.已知=5,则tan α=_____________.
14.在中,,,,为的三等分点,则____________.
15.已知函数是奇函数.若,求的取值范围_________
16.在四面体PABC中,平面平面ABC,,,则该四面体的外接球的体积为___________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.在①,②,③这三个条件中任选一个,补充在下面问题中,并解答.
已知在中,角A,B,C所对的边分别是a,b,c,___________.
(1)求角A; (2)若,,求的面积.
注:如果选择多个条件分别解答,按第一个解答计分.
18.为了调查90后上班族每个月的休假天数,研究人员随机抽取了1000名90后上班族作出调查,所得数据统计如图所示.
(1)求的值以及这1000名90后上班族每个月休假天数的平均数(同一组中的数据用该组区间的中点值作代表);
(2)为研究90后上班族休假天数与月薪的关系,从上述1000名被调查者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有%的把握认为休假天数与月薪有关.
月休假不超过6天 月休假超过6天 合计
月薪超过5000 90
月薪不超过5000 140
合计 300
参考公式:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.已知等比数列的公比和等差数列的公差都为,等比数列的首项为2,且,,成等差数列,等差数列的首项为1.
(1)求和的通项公式;
(2)若数列的前项和为,求.
20.在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(1)求证:AB∥平面DEG;
(2)求二面角C DF E的余弦值.
21.全国高中数学联赛活动旨在通过竞赛的方式,培养中学生对于数学的兴趣,让学生喜爱数学,学习数学,激发学生的钻研精神,独立思考精神以及合作精神.现有同学甲、乙二人积极准备参加数学竞赛选拔,在5次模拟训练中,这两位同学的成绩如下表,假设甲、乙二人每次训练成绩相互独立.
第1次 第2次 第3次 第4次 第5次
甲 86 92 87 89 86
乙 90 86 89 88 87
(1)从5次训练中随机选取1次,求甲的成绩高于乙的成绩的概率;
(2)从5次训练中随机选取2次,用表示甲的成绩高于乙的成绩的次数,求的分布列和数学期望;
(3)根据数据信息,你认为谁在选拔中更具竞争力,并说明理由.
(注:样本数据的方差,其中)
22.已知函数在点处的切线平行于x轴.
(1)求实数a,b的值;
(2)讨论函数的零点个数.
参考答案
1.D【详解】由题知,,则,所以,
故选:D.
2.B【详解】
设此数列前30项和为,则,
故选:B.
3.B【详解】求解二次不等式可得:,
∵ 由可推出,由不能推出,
∴ 是的必要不充分条件.
故选:B.
4.C
【详解】
由题设,,,,,
∴零点所在的区间为(,1).
故选:C
5.C
6.A
7.D【详解】对于选项A中:由A=30°,B=45°,c=5,所以,再利用正弦定理可求,显然只有一解;
对于选项B中:由余弦定理可得,所以只有一解;
对于选项C中:因为,且,所以只有一解;
对于选项D中:因为,且,所以角有两解.
故选:D.
8.C
【详解】由得,,
因函数在内有极值,则时,有解,
即在时,函数与直线y=a有公共点,
而,即在上单调递减,,则,显然在零点左右两侧异号,
所以实数的取值范围是.
故选:C
9.ABD
【详解】
由题知,
所以,
对于A选项,由于在上单调递减,
所以当时,可以得到,故A正确,
对于B选项,因为,不等式两边同乘负数得,
故B正确,
对于C选项,因为,所以,
故C错误,
对于D选项,由于在上单调递增,
所以当时,可以得到,故D正确,
故选:ABD.
10.BC
【详解】
A:,,显然,故的周期为错误;
B:,正确;
C:在上,,易知在区间上递增,正确;
D:,,显然,故关于点中心对称错误;
故选:BC
11.ACD
【详解】
对于选项A,结合正方体的性质,可知,故易得AB平面A1CD,故A正确;
对于选项B, 结合正方体的性质,易知直线与直线都在平面中,故B错误;
对于选项C,取的中点,连接、、、 ,易知,
结合正方体的性质,易知平面,故平面,
即在点处时,平面,故C正确;
对于选项D,取的中点,结合正方体的性质,易知平面,
因此即为直线与平面所成角,
因为 ,,所以,故D正确.
故选:ACD.
12.B
【详解】
由题意可知,则对任意的,,则,,
由,得,,,
,因此,.
故选:B.
13.2
14.
【详解】
设,,
同理,,
由得:,
∴
.
故答案为:.
15.
16.
【详解】
解析:如图,设AB的中点为D,连接PD,DC,因为,,所以,,
又平面平面ABC,所以平面ABC,平面PAB.
设该四面体外接球的球心为O,,的外接圆圆心分别为,,
易知,分别在直线DC,PD上,连接,,则平面ABC,所以,则四边形为矩形.
设,的外接圆半径分别为,,外接球的半径为R,
在中,由正弦定理得,则.
在中,,易得,所以,
所以,得,则,连接PO,
在中,,
所以该四面体的外接球的体积.
故答案为:.
17.
(1)
(2)
(1)方案一:选条件①.
根据正弦定理及得,
整理得,
即,
易知,
所以,
又,所以,
又,(注意角的范围)故.
方案二:选条件②.
在中,,所以,
结合二倍角公式,可得,
所以,
得.
又,所以.
方案三:选条件③.
在中,,所以,
所以,
结合正弦定理可得,,得.
又,所以.
(2)
根据余弦定理可得,
,
又,,,
所以,得,
所以.
18.
(1),这1000名90后上班族每个月休假天数的平均数为6
(2)有%的把握认为休假天数与月薪有关,理由见解析
(1)
因为,所以
这1000名90后上班族每个月休假天数的平均数为
(2)
1000名中月休假不超过6天的总人数为人,
超过6天的总人数为500人,
按分层抽样可得这300人中不超过6天的人数为150人,超过6天的人数为150人
所以
月休假不超过6天 月休假超过6天 合计
月薪超过5000 90 70 160
月薪不超过5000 60 80 140
合计 150 150 300
所以有%的把握认为休假天数与月薪有关.
19.
(1),
(2)
(1)
因为,,成等差数列,所以:,整理得:,
即,故,解得,
所以,.
(2)
证明:(2)由(1)得:,
故①,
②,
①②得:,故.
20.【解】 (1)证明:因为AD∥EF,EF∥BC,
所以AD∥BC,又BC=2AD,G是BC的中点,
所以AD//BG且AD=BG,所以四边形ADGB是平行四边形,所以AB∥DG.
因为AB 平面DEG,DG 平面DEG,
所以AB∥平面DEG.
(2)因为EF⊥平面AEB,AE 平面AEB,BE 平面AEB,
所以EF⊥AE,EF⊥BE,又AE⊥EB,
所以EB,EF,EA两两垂直.
以点E为坐标原点,EB,EF,EA所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系.
则E(0,0,0),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2).
由已知得=(2,0,0)是平面EFDA的一个法向量.
设平面DCF的法向量为n=(x,y,z),
则因为=(0,-1,2),=(2,1,0),所以令z=1,得y=2,x=-1,所以可取n=(-1,2,1).
设二面角C DF E的大小为θ,则cos θ=cos〈n,〉==-.
易知二面角C DF E为钝二面角,
所以二面角C DF E的余弦值为-.
21.
(1);
(2)分布列见解析,数学期望为;
(3)乙在选拔中更具竞争力,理由见解析.
(1)
在5次模拟训练中,甲的成绩高于乙的成绩有2次,乙的成绩高于甲的成绩有3次,
从5次训练中随机选取1次的试验有5个基本事件,它们等可能,甲的成绩高于乙的成绩的事件A有2个基本事件,
所以甲的成绩高于乙的成绩的概率.
(2)
的所有可能值是:0,1,2,
,,,
所以的分布列为:
0 1 2
数学期望为.
(3)
甲的平均成绩为,
乙的平均成绩为,
甲成绩的方差,
乙成绩的方差,
虽然,但,因此得乙的成绩更稳定,
所以乙在选拔中更具竞争力.
22.
(1)
(2)函数在上有两个零点.
(1)
因为,所以,
由题意可知,解得,
(2)
由(1)知,所以,
由于,所以当时,,所以在上单调递增,因为时,,而,因此时,,因此函数在上无零点;
则,当时,,则在上单调递减,且,因为,则,由零点存在性知在上存在唯一零点;
当时 ,令,则,所以在上单调递增,且,,由零点存在性定理知存在唯一零点,使得,因此在时单调递减,在时单调递增,且,,,由零点存在性定理知存在唯一零点在上,因此在上存在唯一零点;
当时,,则在上单调递增,且,所以在上无零点;
综上所述:函数在上有两个零点.
同课章节目录
