沪科版数学七年级上册 3.2 一元一次方程的应用 教案
文档属性
| 名称 | 沪科版数学七年级上册 3.2 一元一次方程的应用 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 571.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 16:32:14 | ||
图片预览




文档简介
教学课题:3.2一元一次方程的应用
重 难 点 部 分 教 学 过 程 预 设
课前互动 师:我们这里被誉为“水果之乡”,盛产哪些美味可口的水果呀? 生:酥梨、苹果、黄桃…… 师:从同学们的回答中我听到了你们对家乡满满的热爱以及自豪之情.今天我们来学习一下“有关水果”的一些知识. 生:额……和水果有什么关系(好奇)
天平称水果游戏 类型一 : 等积变形问题 一、创设情境,引入新课
教师活动 学生活动 设计意图
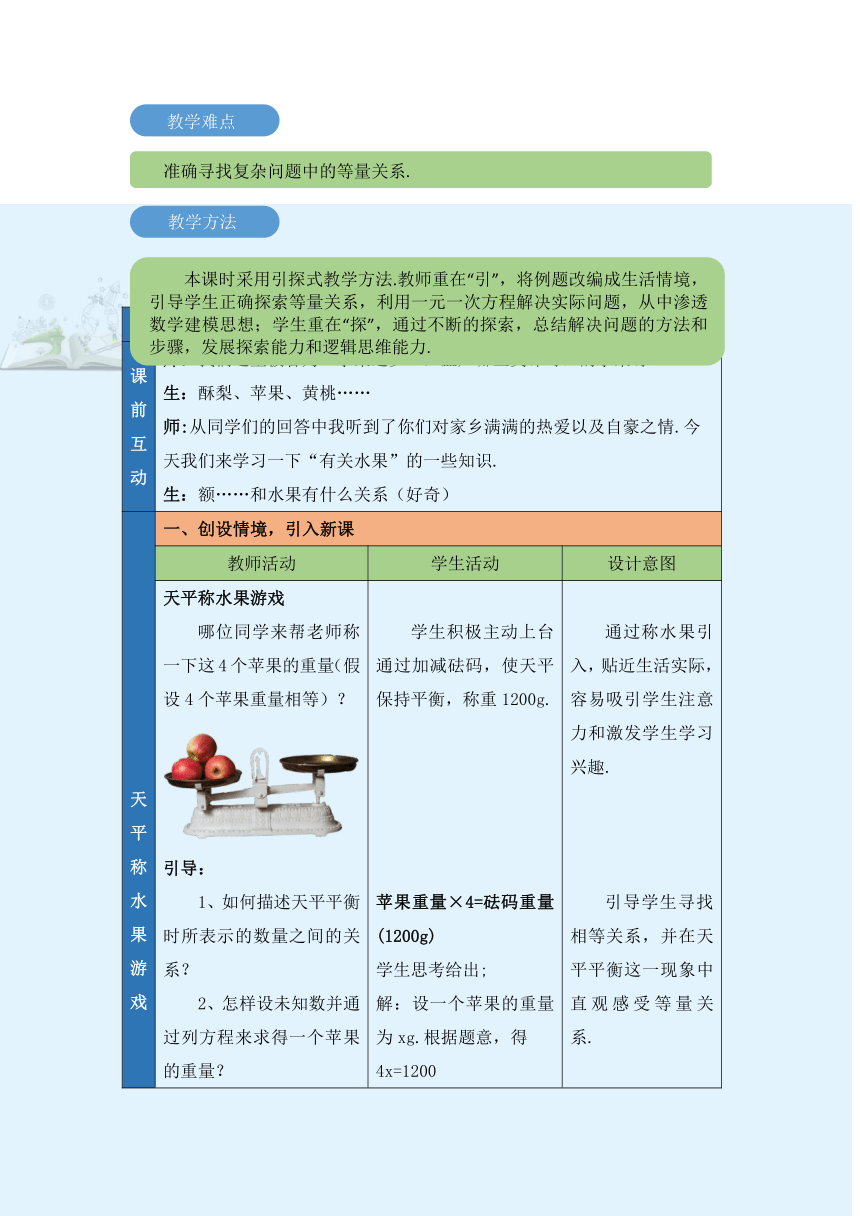
天平称水果游戏 哪位同学来帮老师称一下这4个苹果的重量(假设4个苹果重量相等)? 引导: 1、如何描述天平平衡时所表示的数量之间的关系? 2、怎样设未知数并通过列方程来求得一个苹果的重量? 学生积极主动上台通过加减砝码,使天平保持平衡,称重1200g. 苹果重量×4=砝码重量(1200g) 学生思考给出; 解:设一个苹果的重量为xg.根据题意,得 4x=1200 解得x=300 答:一个苹果的重量为300g. 通过称水果引入,贴近生活实际,容易吸引学生注意力和激发学生学习兴趣. 引导学生寻找相等关系,并在天平平衡这一现象中直观感受等量关系.
变式训练: 1、称2个重量相等梨子和一个果盘(200g) 2、天平左边放5个苹果,右侧放2个苹果(所有苹果重量相等),让学生通过在右侧添加砝码,调节平衡. 部分学生上讲台调整砝码,其他学生尝试口答上述两个问题. 让学生在动手实践、直观体验中多停留,以便更深入感受等量关系. 同时增加了学生学习的兴趣.
二、合作交流,探索新知
教师活动 学生活动 设计意图
环节一:称水果 (改编自例1:等积变形问题)张大伯用直径为200mm的圆柱体水桶装满油桃(忽略空隙),在称重时将油桃放入一个长、宽、高分别是300mm,300mm和90mm的长方体纸箱中,正好装满(忽略空隙)。问张大伯的圆柱体水桶高度是多少毫米?(计算时π取3.14,结果精确到1 mm) 引导: 1、在放入的过程中哪些量改变了?哪些量没变? 2、如何通过列方程来解决问题? 学生思考给出引导1:把圆柱体水桶的油桃放入长方体纸盒中,虽然形状发生了变化,但放入前后的体积是相等的,也就是 圆柱体水桶体积=长方体纸盒体积 学生先独立思考,然后小组内讨论,计算给出引导2: 解:设张大伯的的圆柱体水桶高度是x mm. 根据题意,得 3.14×() x=300×300×90, 解得x≈258. 答:张大伯的圆柱体水桶的高度为258 ㎜. 生活化的改编,利于理解. 引导学生在改变的过程中寻找不变的量:等量关系 通过独立思考,小组合作的形式,培养学生良好的思维习惯和合作意识.
变式训练: 将一个长、宽、高分别为12㎝,6㎝,47㎝的长方体铁块和一个棱长为6㎝的正方体铁块熔成一个底面边长均为15㎝的长方体,求这个长方体的高. 学生先探索等量关系:长方体铁块体积+正方体铁块体积=大长方体铁块体积 并根据等量关系列方程求解. 变式未做改编,回归书本题目,检测学生学习的真实效果.
类 型二 : 行程问题 类 型二 : 行程问题 教师活动 学生活动 设计意图
环节二:运水果 (改编自例2行程问题)为了将水果快速运出,货车运输再次提速.如果货车行驶的平均速度增加20 km/h,提速后由本地到北京800 km的路程只需行驶10h.那么,提速前,这趟货车平均每时行驶多少千米? 引导: 1、行程问题中常涉及的量有哪些?它们之间有什么关系? 2、你能否找出本题的等量关系式?本题如何求解? 学生思考后回答:行程问题中常涉及的量有路程、平均速度和时间,它们之间的基本关系为: 路程=平均速度×时间 解:设提速前货车平均每时行驶x km,那么提速后货车平均每时行驶(x+20) km,货车行驶路程800 km,所需时间是10 h. 根据题意,得 10(x+20)=800. 解方程,得x=60. 答:提速前这趟货车的平均速度是60km/h. 将例题做适当的改编,既符合教材内容,又避免学生已经通过预习知道答案. 让学生感受解决行程问题的关键是找到等量关系式.同时通过水果运往各地,给他人带来美味的享受,提升学生的自豪感.
变式练习: 1、相遇问题 甲、乙两地相距180 km,一人骑自行车从甲地出发每小时行15 km;另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车车速是自行车车速的3倍,问多少时间后两人相遇? 引导:在分析行程问题中,有时线段示意图的使用利于理解题意和准确寻找等量关系. 2、追及问题 敌我两军相距25 km,敌军以5 km/h的速度逃跑,我军同时以8 km/h的速度追击,并在相距1 km处发生战斗,问战斗是在开始追击后几小时发生的? 学生独立思考,尝试画出线段图,帮助解答. 线段示意图: 15xkm 15×3xkm
甲 乙 180km 等量关系式: 骑自行车路程(15x)+骑摩托车路程(3×15x)=总路程(180) 解答略 学生通过探索等量关系式,列方程解出. 一部分学生使用线段示意图,一部分同学未使用. 在分析一些较复杂行程问题时,线段示意图的使用,很直观帮助学生准确找到等量关系.例2未使用,变式补充给出. 通过两种变式作为巩固,帮助学生掌握解决行程问题的方法.
解题步骤小结 师生活动 设计意图
师:通过以上学习,同学们来总结一下列方程解应用题的一般步骤? 学生通过回顾学习过程,总结得出. (1)弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数; (2)分析题意,找出相等关系(可借助于示意图、表格等); (3)根据相等关系,列出需要的代数式,并列出方程; (4)解这个方程,求出未知数的值; (5)检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称). 让学生自己回顾学习过程,自主归纳解题步骤,利于学生加深对知识的理解和总结概括能力的培养.
类型三 : 销售问题 教师活动 学生活动 设计意图
环节三:卖水果 (改编自例4:销售问题)某商店出售苹果时,按进价提高50%作为标价,然后再按标价9折出售,这样商店每卖出一千克可盈利2.1元.问这种苹果每千克进价多少? 引导: 1、销售问题中常涉及的量有哪些?它们之间有什么关系? 2、你能找出本题的等量关系式吗?本题如何求解? 学生回顾所学,回答:销售中常涉及的量有利润、售价、进价等。 本题等量关系式: 利润=实际售价-进价 解:设苹果每千克进价为x元,那么苹果每千克的标价为(1+50%)x,对它打9折得实际售价为×(1+50%)x. 根据题意,得 ×(1+50%)x-x=2.1. 解这个方程,得x=6. 答:这种苹果每千克进价为6元. 将“例4”改编为“卖水果”,和前后相呼应,易于理解. 解决销售问题的关键是找到等量关系式.同时应注意避免学生混淆有些概念,比如此题提价后为标价,打折后才是实际售价.
变式训练: 一件夹克衫,按进价提高5成作为定价,后因季节关系,按定价的8折出售,打折后每件卖60元,试问这批夹克每件的成本价是多少元? 学生通过探索等量关系式,列方程解出. 部分学生对“提高5成”、“8折出售”的理解存在困难,通过小组合作解除疑惑. 让学生感受类似的“打折销售”、“大酬宾”、“大削价”等广告,实际上都是先升后降.
类型四 : 储蓄问题 教师活动 学生活动 设计意图
环节四:存水果收入 (改编自例3:储蓄问题)张大伯把卖水果的一笔钱作为3年定期存款存入银行,年利率为5%.到期后预计可得到本息共11500元,问张大伯存入银行多少钱? 引导: 1、储蓄问题中常涉及的量有哪些?它们之间有什么关系? 2、你能找出本题的等量关系式吗?本题如何求解? 学生思考后积极回答:储蓄问题中常涉及的量有本金、利率、利息、本息等. 本题的等量关系式: 利息=本金×利率×年数 本金+利息=本息和. 解:设张大伯存入银行x元,年利率为5%,存期3年,所以预期3年的利息为3×5%x元.3年到期后的本息共为11500元. 根据题意,得 x+3×5%x=11500. 解方程,得x=10000. 答:张大伯存入银行10000元. 学生在六年级学过利率,只要对相关知识温习一下,再根据题意找出等量关系和关键词,设出未知数列出方程即可迎刃而解.
变式训练: 张师傅在银行里用定期一年整存整取的方式存入人民币8000元,到期得到本息8180元,求这项储蓄的月利率(不计利息税). 学生通过探索等量关系式,列方程解出. 部分学生对“月利率”和“年利率”这两个概念易混淆,后经过教师引导和与同学交流分清两者区别。 存款利率问题中有很多相关联的量,鼓励学生对公式进行变形推导,培养学生推理能力. 在教学中渗透数学的实用性.
类型五 : 比例问题 教师活动 学生活动 设计意图
环节五:灌溉果林 (改编自例5:比例问题)张大伯等三个家庭共同使用水泵灌溉果林,如果三个家庭灌溉的土地面积之比为4∶5∶6,而这一次装运水泵和耗用的电力费用共计240元,三个家庭按土地面积比各应该负担多少元? 引导: 1、各个家庭应负担的费用和什么有关? 2、你能找出本题的等量关系式吗?本题应该怎么设未知数呢?怎样求解? 学生经过小组讨论得:各个家庭应负担费用与灌溉的土地面积成正比,且三个家庭各自应负担费用之和等于240元.由于共有土地4+5+6=15份,因而240元可由15份分担 等量关系式: 一家庭负担费用+二家庭负担费用+三家庭负担费用=总负担费用 解:设每份土地灌溉分担费用x元,那么三个家庭应负担费用分别为4x元、5x元、6x元. 根据题意,得 4x+5x+6x=240, 解方程,得x=16. 4x=64,5x=80,6x=96. 答:三个家庭各应负担64元、80元、96元. 引导学生理解 “设每份土地灌溉分担费用x元”属间接设未知数法.当不能或难以直接设未知数时,间接设未知数是一种有效途径. 同时通过合作灌溉的例子,引导学生理解合作的实用性,渗透合作意识.
变式训练: 长方形的长与宽之比为5:2,它的周长为56厘米,求这个长方形的面积. 部分学生忽略长方形有两个长与宽. 及时练习,巩固所学.
巩固练习 三、达标测试,应用提高
师生活动 设计意图
1、若将底面直径为10dm、高为8dm的钢材,锻造成底面直径为4dm的钢材,问钢材长多少dm 2、通讯员原计划用5h从甲地到乙地,因任务紧急,他每时比原计划快3km,结果提前1h到达,求甲乙两地间的距离. 3、张宏在商场买一种商品.如买9件,则所带钱差3.5元;如买8件,尚余2.5元。问张宏带了多少钱? 4、爸爸为小亮存了一笔钱,为期5年。5年后本息共6375元,小亮的爸爸当时存入了多少元?(当时的5年储蓄的年利率为5.5%) 5、兄弟两人合伙从事经营,哥哥入股25000元,弟弟入股20000元,一年后盈利8352元。按入股的资金比例分配,兄弟两人各应分得盈利多少元? 5题对应5种类型,让学生独立完成,巩固所学的内容,同时反馈学习效果,有利于教师及时了解教学情况.
课堂小结 四、自主梳理,感悟收获
教师活动 学生活动 设计意图
请同学们说说今天你有什么收获? 学生经过思考和交流后,分享自己的收获. 让学生自己回顾、梳理知识,利于加深学生对知识的理解和思维严谨性的培养
作业布置 五、基于学情,作业分层
师生活动 设计意图
1、必做作业 书本习题3.2第1,5,6题. 基础训练3.2. 2、选做作业 甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分. (1)两人同时同地同向跑,问第一次相遇时,两人一共跑了多少圈? (2)两人同时同地反向跑,问几秒后两人第一次相遇? 分层设置作业,使不同基础的学生都能得到很好的发展.
板书设计 3.2 一元一次方程的应用 一、创设情境,引入新课. 天平称水果游戏 二、合作交流,探索新知. 环节一:称水果——等积变形问题 环节二:运水果——行程问题 环节三:卖水果——销售问题 环节四:存水果收入——储蓄问题 环节五:灌溉果林——比例问题 三、达标测试,应用提高. 四、自主梳理,感悟收获. 五、基于学情,作业分层.
课后小结 本节课预设受教学生群体,根据学生的知识基础、年龄特征、生活环境,设计切合实际、贴近生活的实例.使学生在教师的引导下,通过独立思考、小组合作的形式探索具体情境中的等量关系,并运用一元一次方程求解。同时,在教学的过程中,激发学生的学习兴趣,培养学生的探究推理能力,发展学生的逻辑思维能力.让学生感受数学建模思想,体验成功的喜悦,体会数学的实用性. 但部分环节设置不够流畅,引导的语言组织的不够准确、到位,整体设计略显仓促.
重 难 点 部 分 教 学 过 程 预 设
课前互动 师:我们这里被誉为“水果之乡”,盛产哪些美味可口的水果呀? 生:酥梨、苹果、黄桃…… 师:从同学们的回答中我听到了你们对家乡满满的热爱以及自豪之情.今天我们来学习一下“有关水果”的一些知识. 生:额……和水果有什么关系(好奇)
天平称水果游戏 类型一 : 等积变形问题 一、创设情境,引入新课
教师活动 学生活动 设计意图
天平称水果游戏 哪位同学来帮老师称一下这4个苹果的重量(假设4个苹果重量相等)? 引导: 1、如何描述天平平衡时所表示的数量之间的关系? 2、怎样设未知数并通过列方程来求得一个苹果的重量? 学生积极主动上台通过加减砝码,使天平保持平衡,称重1200g. 苹果重量×4=砝码重量(1200g) 学生思考给出; 解:设一个苹果的重量为xg.根据题意,得 4x=1200 解得x=300 答:一个苹果的重量为300g. 通过称水果引入,贴近生活实际,容易吸引学生注意力和激发学生学习兴趣. 引导学生寻找相等关系,并在天平平衡这一现象中直观感受等量关系.
变式训练: 1、称2个重量相等梨子和一个果盘(200g) 2、天平左边放5个苹果,右侧放2个苹果(所有苹果重量相等),让学生通过在右侧添加砝码,调节平衡. 部分学生上讲台调整砝码,其他学生尝试口答上述两个问题. 让学生在动手实践、直观体验中多停留,以便更深入感受等量关系. 同时增加了学生学习的兴趣.
二、合作交流,探索新知
教师活动 学生活动 设计意图
环节一:称水果 (改编自例1:等积变形问题)张大伯用直径为200mm的圆柱体水桶装满油桃(忽略空隙),在称重时将油桃放入一个长、宽、高分别是300mm,300mm和90mm的长方体纸箱中,正好装满(忽略空隙)。问张大伯的圆柱体水桶高度是多少毫米?(计算时π取3.14,结果精确到1 mm) 引导: 1、在放入的过程中哪些量改变了?哪些量没变? 2、如何通过列方程来解决问题? 学生思考给出引导1:把圆柱体水桶的油桃放入长方体纸盒中,虽然形状发生了变化,但放入前后的体积是相等的,也就是 圆柱体水桶体积=长方体纸盒体积 学生先独立思考,然后小组内讨论,计算给出引导2: 解:设张大伯的的圆柱体水桶高度是x mm. 根据题意,得 3.14×() x=300×300×90, 解得x≈258. 答:张大伯的圆柱体水桶的高度为258 ㎜. 生活化的改编,利于理解. 引导学生在改变的过程中寻找不变的量:等量关系 通过独立思考,小组合作的形式,培养学生良好的思维习惯和合作意识.
变式训练: 将一个长、宽、高分别为12㎝,6㎝,47㎝的长方体铁块和一个棱长为6㎝的正方体铁块熔成一个底面边长均为15㎝的长方体,求这个长方体的高. 学生先探索等量关系:长方体铁块体积+正方体铁块体积=大长方体铁块体积 并根据等量关系列方程求解. 变式未做改编,回归书本题目,检测学生学习的真实效果.
类 型二 : 行程问题 类 型二 : 行程问题 教师活动 学生活动 设计意图
环节二:运水果 (改编自例2行程问题)为了将水果快速运出,货车运输再次提速.如果货车行驶的平均速度增加20 km/h,提速后由本地到北京800 km的路程只需行驶10h.那么,提速前,这趟货车平均每时行驶多少千米? 引导: 1、行程问题中常涉及的量有哪些?它们之间有什么关系? 2、你能否找出本题的等量关系式?本题如何求解? 学生思考后回答:行程问题中常涉及的量有路程、平均速度和时间,它们之间的基本关系为: 路程=平均速度×时间 解:设提速前货车平均每时行驶x km,那么提速后货车平均每时行驶(x+20) km,货车行驶路程800 km,所需时间是10 h. 根据题意,得 10(x+20)=800. 解方程,得x=60. 答:提速前这趟货车的平均速度是60km/h. 将例题做适当的改编,既符合教材内容,又避免学生已经通过预习知道答案. 让学生感受解决行程问题的关键是找到等量关系式.同时通过水果运往各地,给他人带来美味的享受,提升学生的自豪感.
变式练习: 1、相遇问题 甲、乙两地相距180 km,一人骑自行车从甲地出发每小时行15 km;另一人骑摩托车从乙地同时出发,两人相向而行,已知摩托车车速是自行车车速的3倍,问多少时间后两人相遇? 引导:在分析行程问题中,有时线段示意图的使用利于理解题意和准确寻找等量关系. 2、追及问题 敌我两军相距25 km,敌军以5 km/h的速度逃跑,我军同时以8 km/h的速度追击,并在相距1 km处发生战斗,问战斗是在开始追击后几小时发生的? 学生独立思考,尝试画出线段图,帮助解答. 线段示意图: 15xkm 15×3xkm
甲 乙 180km 等量关系式: 骑自行车路程(15x)+骑摩托车路程(3×15x)=总路程(180) 解答略 学生通过探索等量关系式,列方程解出. 一部分学生使用线段示意图,一部分同学未使用. 在分析一些较复杂行程问题时,线段示意图的使用,很直观帮助学生准确找到等量关系.例2未使用,变式补充给出. 通过两种变式作为巩固,帮助学生掌握解决行程问题的方法.
解题步骤小结 师生活动 设计意图
师:通过以上学习,同学们来总结一下列方程解应用题的一般步骤? 学生通过回顾学习过程,总结得出. (1)弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数; (2)分析题意,找出相等关系(可借助于示意图、表格等); (3)根据相等关系,列出需要的代数式,并列出方程; (4)解这个方程,求出未知数的值; (5)检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称). 让学生自己回顾学习过程,自主归纳解题步骤,利于学生加深对知识的理解和总结概括能力的培养.
类型三 : 销售问题 教师活动 学生活动 设计意图
环节三:卖水果 (改编自例4:销售问题)某商店出售苹果时,按进价提高50%作为标价,然后再按标价9折出售,这样商店每卖出一千克可盈利2.1元.问这种苹果每千克进价多少? 引导: 1、销售问题中常涉及的量有哪些?它们之间有什么关系? 2、你能找出本题的等量关系式吗?本题如何求解? 学生回顾所学,回答:销售中常涉及的量有利润、售价、进价等。 本题等量关系式: 利润=实际售价-进价 解:设苹果每千克进价为x元,那么苹果每千克的标价为(1+50%)x,对它打9折得实际售价为×(1+50%)x. 根据题意,得 ×(1+50%)x-x=2.1. 解这个方程,得x=6. 答:这种苹果每千克进价为6元. 将“例4”改编为“卖水果”,和前后相呼应,易于理解. 解决销售问题的关键是找到等量关系式.同时应注意避免学生混淆有些概念,比如此题提价后为标价,打折后才是实际售价.
变式训练: 一件夹克衫,按进价提高5成作为定价,后因季节关系,按定价的8折出售,打折后每件卖60元,试问这批夹克每件的成本价是多少元? 学生通过探索等量关系式,列方程解出. 部分学生对“提高5成”、“8折出售”的理解存在困难,通过小组合作解除疑惑. 让学生感受类似的“打折销售”、“大酬宾”、“大削价”等广告,实际上都是先升后降.
类型四 : 储蓄问题 教师活动 学生活动 设计意图
环节四:存水果收入 (改编自例3:储蓄问题)张大伯把卖水果的一笔钱作为3年定期存款存入银行,年利率为5%.到期后预计可得到本息共11500元,问张大伯存入银行多少钱? 引导: 1、储蓄问题中常涉及的量有哪些?它们之间有什么关系? 2、你能找出本题的等量关系式吗?本题如何求解? 学生思考后积极回答:储蓄问题中常涉及的量有本金、利率、利息、本息等. 本题的等量关系式: 利息=本金×利率×年数 本金+利息=本息和. 解:设张大伯存入银行x元,年利率为5%,存期3年,所以预期3年的利息为3×5%x元.3年到期后的本息共为11500元. 根据题意,得 x+3×5%x=11500. 解方程,得x=10000. 答:张大伯存入银行10000元. 学生在六年级学过利率,只要对相关知识温习一下,再根据题意找出等量关系和关键词,设出未知数列出方程即可迎刃而解.
变式训练: 张师傅在银行里用定期一年整存整取的方式存入人民币8000元,到期得到本息8180元,求这项储蓄的月利率(不计利息税). 学生通过探索等量关系式,列方程解出. 部分学生对“月利率”和“年利率”这两个概念易混淆,后经过教师引导和与同学交流分清两者区别。 存款利率问题中有很多相关联的量,鼓励学生对公式进行变形推导,培养学生推理能力. 在教学中渗透数学的实用性.
类型五 : 比例问题 教师活动 学生活动 设计意图
环节五:灌溉果林 (改编自例5:比例问题)张大伯等三个家庭共同使用水泵灌溉果林,如果三个家庭灌溉的土地面积之比为4∶5∶6,而这一次装运水泵和耗用的电力费用共计240元,三个家庭按土地面积比各应该负担多少元? 引导: 1、各个家庭应负担的费用和什么有关? 2、你能找出本题的等量关系式吗?本题应该怎么设未知数呢?怎样求解? 学生经过小组讨论得:各个家庭应负担费用与灌溉的土地面积成正比,且三个家庭各自应负担费用之和等于240元.由于共有土地4+5+6=15份,因而240元可由15份分担 等量关系式: 一家庭负担费用+二家庭负担费用+三家庭负担费用=总负担费用 解:设每份土地灌溉分担费用x元,那么三个家庭应负担费用分别为4x元、5x元、6x元. 根据题意,得 4x+5x+6x=240, 解方程,得x=16. 4x=64,5x=80,6x=96. 答:三个家庭各应负担64元、80元、96元. 引导学生理解 “设每份土地灌溉分担费用x元”属间接设未知数法.当不能或难以直接设未知数时,间接设未知数是一种有效途径. 同时通过合作灌溉的例子,引导学生理解合作的实用性,渗透合作意识.
变式训练: 长方形的长与宽之比为5:2,它的周长为56厘米,求这个长方形的面积. 部分学生忽略长方形有两个长与宽. 及时练习,巩固所学.
巩固练习 三、达标测试,应用提高
师生活动 设计意图
1、若将底面直径为10dm、高为8dm的钢材,锻造成底面直径为4dm的钢材,问钢材长多少dm 2、通讯员原计划用5h从甲地到乙地,因任务紧急,他每时比原计划快3km,结果提前1h到达,求甲乙两地间的距离. 3、张宏在商场买一种商品.如买9件,则所带钱差3.5元;如买8件,尚余2.5元。问张宏带了多少钱? 4、爸爸为小亮存了一笔钱,为期5年。5年后本息共6375元,小亮的爸爸当时存入了多少元?(当时的5年储蓄的年利率为5.5%) 5、兄弟两人合伙从事经营,哥哥入股25000元,弟弟入股20000元,一年后盈利8352元。按入股的资金比例分配,兄弟两人各应分得盈利多少元? 5题对应5种类型,让学生独立完成,巩固所学的内容,同时反馈学习效果,有利于教师及时了解教学情况.
课堂小结 四、自主梳理,感悟收获
教师活动 学生活动 设计意图
请同学们说说今天你有什么收获? 学生经过思考和交流后,分享自己的收获. 让学生自己回顾、梳理知识,利于加深学生对知识的理解和思维严谨性的培养
作业布置 五、基于学情,作业分层
师生活动 设计意图
1、必做作业 书本习题3.2第1,5,6题. 基础训练3.2. 2、选做作业 甲、乙两人在一条长400米的环形跑道上跑步,甲的速度为360米/分,乙的速度是240米/分. (1)两人同时同地同向跑,问第一次相遇时,两人一共跑了多少圈? (2)两人同时同地反向跑,问几秒后两人第一次相遇? 分层设置作业,使不同基础的学生都能得到很好的发展.
板书设计 3.2 一元一次方程的应用 一、创设情境,引入新课. 天平称水果游戏 二、合作交流,探索新知. 环节一:称水果——等积变形问题 环节二:运水果——行程问题 环节三:卖水果——销售问题 环节四:存水果收入——储蓄问题 环节五:灌溉果林——比例问题 三、达标测试,应用提高. 四、自主梳理,感悟收获. 五、基于学情,作业分层.
课后小结 本节课预设受教学生群体,根据学生的知识基础、年龄特征、生活环境,设计切合实际、贴近生活的实例.使学生在教师的引导下,通过独立思考、小组合作的形式探索具体情境中的等量关系,并运用一元一次方程求解。同时,在教学的过程中,激发学生的学习兴趣,培养学生的探究推理能力,发展学生的逻辑思维能力.让学生感受数学建模思想,体验成功的喜悦,体会数学的实用性. 但部分环节设置不够流畅,引导的语言组织的不够准确、到位,整体设计略显仓促.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
