华东师大版数学七年级上册 2.9有理数的乘法 教案
文档属性
| 名称 | 华东师大版数学七年级上册 2.9有理数的乘法 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 53.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览

文档简介
“有理数乘法”教案
一、课题
华东师大七年级(上)第二章第9节内容有理数乘法(第一课时).
二、学习目标
1.知识与技能目标:理解有理数乘法法则,能进行合理运算.
2.过程与方法目标:让学生观察、分析实际问题,自主探索,发现规律.
3.情感态度与价值目标:培养学生实事求是的科学态度,让学生在合作、交流中愉悦学习,分享成功的快乐,通过学生发现规律,运用规律,培养学生勇于探索的精神和学以致用的价值观.
三、学习重点、难点及关键
重点:理解有理数乘法法则.
难点:负有理数的乘法
关键:确定积的符号
四、学习过程
(一)创设情境,引发认知冲突
情境一(多媒体演示;规定向东为正,向西为负;下同)
一只玩具小汽车沿东西方向的路线从O点出发行驶,以每分钟5米的速度向东行驶2分钟,此时,它位于原来位置的哪个方向?相距多远?如何求解?若将时间改成3分钟和4分钟呢?(学生思考、作答)
情境二(略)
(二)新知导学
1.大胆探索,形成规律
回想在情境二的式子中,该如何计算其结果呢?
探究一:引导学生用加法运算:
探究二:比较下面两组算式中左边的因数有什么不同,右边得到的积又有什么不同?从中发现什么规律?并用语言表述.
让学生充分讨论,自己探索,抽取学生发表见解,得出如下结论:
两数相乘,把一因数换成它的相反数,所得的积是原来积的相反数.
试一试(略)
2.探讨规律,导出法则
探究三:
(1) (2)
同
号
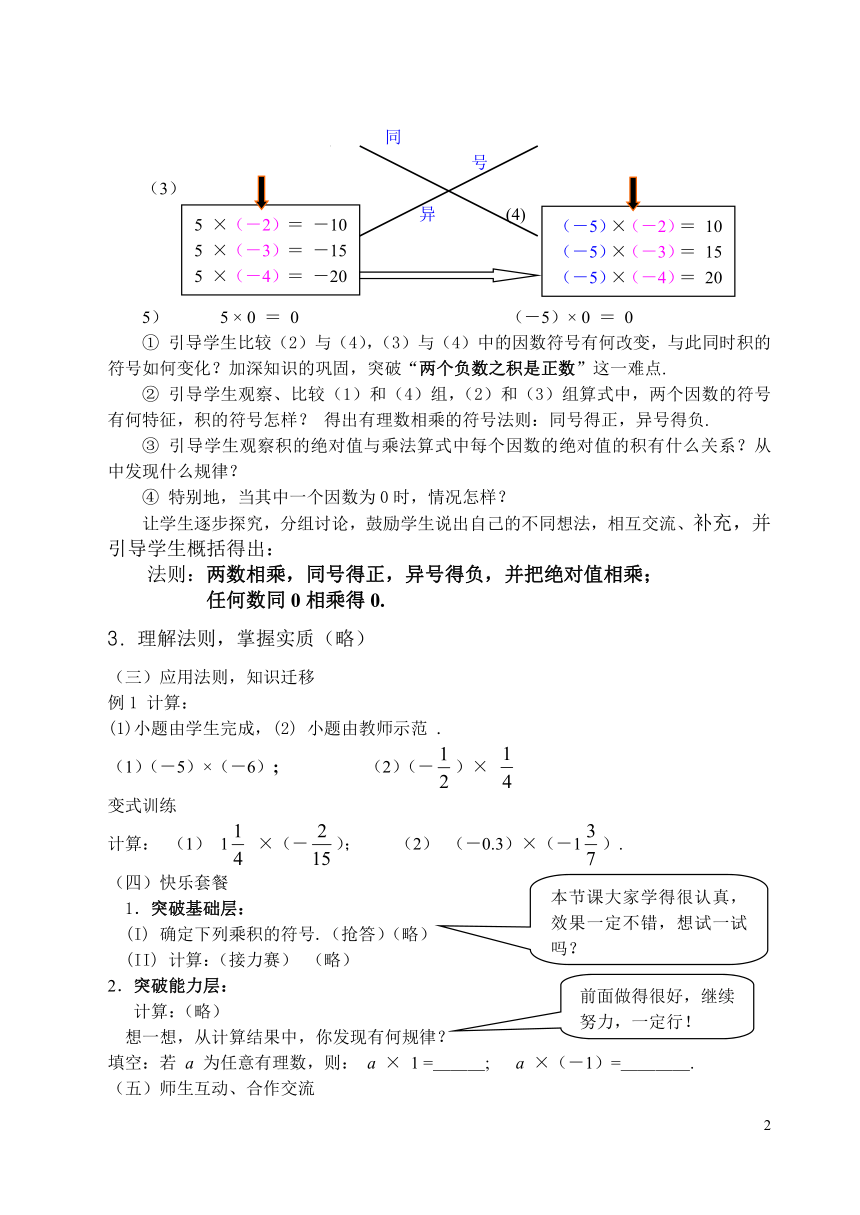
(3)
异 (4)
5) 5 × 0 = 0 (-5)× 0 = 0
① 引导学生比较(2)与(4),(3)与(4)中的因数符号有何改变,与此同时积的符号如何变化?加深知识的巩固,突破“两个负数之积是正数”这一难点.
② 引导学生观察、比较(1)和(4)组,(2)和(3)组算式中,两个因数的符号有何特征,积的符号怎样? 得出有理数相乘的符号法则:同号得正,异号得负.
③ 引导学生观察积的绝对值与乘法算式中每个因数的绝对值的积有什么关系?从中发现什么规律?
④ 特别地,当其中一个因数为0时,情况怎样?
让学生逐步探究,分组讨论,鼓励学生说出自己的不同想法,相互交流、补充,并引导学生概括得出:
法则:两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘得0.
3. 理解法则,掌握实质(略)
(三)应用法则,知识迁移
例1 计算:
(1)小题由学生完成,(2) 小题由教师示范 .
(1)(-5)×(-6); (2)(-)×
变式训练
计算: (1) 1 ×(-); (2) (-0.3)×(-1).
(四)快乐套餐
1.突破基础层:
(I) 确定下列乘积的符号.(抢答)(略)
(II) 计算:(接力赛) (略)
2.突破能力层:
计算:(略)
想一想,从计算结果中,你发现有何规律?
填空:若 a 为任意有理数,则: a × 1 =___; a ×(-1)=____.
(五)师生互动、合作交流
教师说明要求, 围绕今天所学内容, 让同桌学生相互出题,给对方计算,不能超出范围.
(六)点金帚(归纳小结)
1. 法则:两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘得0.
2 . 步骤:(1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值.
3. 关键:确定积的符号 同号得正,异号得负.
(七)作业
(学有余力的学生全做,其余学生不做补充.)P52 练习 1、2 ; P57 习题 1、2 .
补充:
1. 沉思阁:
(1) 若 ab < 0, b > 0, 则 a 0. (填“<” “=” “>”).
(2) 若 ab > 0, 则 a、b 满足条件 .
(3)选择:有理数a、b在数轴上位置如图: a 0 b
下列各式正确的是( )
A. a+b > 0 B. b-a < 0 C. ab < 0 D. | b | > | a |
2. 课后拓展:
观察下列各式,它们的积是正是负?
(1)(-2)×(+3)×(+4)×(+5);
(2)(-2)×(-3)×(+4)×(+5);
(3)(-2)×(-3)×(-4)×(+5);
(4)(-2)×(-3)×(-4)×(-5).
3. 课后思考(一):
(-1)×(-1)×…×(-1)+(-1)×(-1)×…×(-1)
2003个(-1) 2004个(-1)
如何计算呢?
课后思考(二)(略)
五、设计思路
本节教学围绕“层层设问→自主探索→发现规律→归纳运用”这一主线展开,对教材内容进行了优化组合,体现了知识的来龙去脉,思路清晰、流畅.在教与学的过程中,创设情境,设置探究问题,学生自主探索、交流合作,而发现规律,进而归纳运用. 充分调动学生自主学习、自主探索的积极性,让学生学会学习、学会探索、学会创新,体现了学生的主体作用. 进而充分体现学生是学习的主人,教师是主导这一教育理念的引路人. 同时,关注学生个性品质的发展培养,及情感态度的发挥. 从而培养学生的团结协作精神,竞争意识,融知识教学和能力培养于一体. 较好的体现了现代教育理念,实施素质教育.因此,学生能理解法则及运用法则.
板书设计
2.9 有理数的乘法(1)
情境 HYPERLINK "http://www.1230.org" 一: 一只玩具小汽车沿东方 小结: 例题
向的路线,从o点出发以每分钟 例1 计算:
5米的速度向东行驶2分钟,此时, 法则: (1)(-5)×(-6); (2)(-)× .
它位于原来位置的哪个方向?相距 两数相乘,同号得正,异号得负, 解:原式 = +(5×6) 解:原式 = -(×)
多远?若将时间改为3、4分钟呢? 并把绝对值相乘; = +30 = -
情境二: 任何数与零相乘,都得零. 变式训练
比较: 计算: (1) 1×(-); (2)(-0.3)×(-1).
步骤:(1)先确定积的符号;
(2)再确定积的绝对值. 巩固与反馈:1、2、3 .
结论:两数相乘,把一个因数换成
它的相反数,所得的积是原来积的 关键:确定积的符号 同号得正, 作业:P52 练习1、2; P57 习题 1、2 .
相反数. 异号得负. 补充: 1 、2、3 .
(-5)×2 = -10
(-5)×3 = -15
(-5)×4 = -20
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
(-5)× 2 = -10
(-5)× 3 = -15
(-5)× 4 = -20
5 ×(-2)= -10
5 ×(-3)= -15
5 ×(-4)= -20
(-5)×(-2)= 10
(-5)×(-3)= 15
(-5)×(-4)= 20
(-5)×2=-10
(-5)×3=-15
(-5)×4=-20
5×3=15
5×4=20
本节课大家学得很认真,效果一定不错,想试一试吗?
前面做得很好,继续努力,一定行!
5 × 2 =10
5 × 3 =15
5 × 4 =20
(-5)× 2 = - 1 0
(-5)× 3 = - 1 5
(-5)× 4 = - 2 0
PAGE
4
一、课题
华东师大七年级(上)第二章第9节内容有理数乘法(第一课时).
二、学习目标
1.知识与技能目标:理解有理数乘法法则,能进行合理运算.
2.过程与方法目标:让学生观察、分析实际问题,自主探索,发现规律.
3.情感态度与价值目标:培养学生实事求是的科学态度,让学生在合作、交流中愉悦学习,分享成功的快乐,通过学生发现规律,运用规律,培养学生勇于探索的精神和学以致用的价值观.
三、学习重点、难点及关键
重点:理解有理数乘法法则.
难点:负有理数的乘法
关键:确定积的符号
四、学习过程
(一)创设情境,引发认知冲突
情境一(多媒体演示;规定向东为正,向西为负;下同)
一只玩具小汽车沿东西方向的路线从O点出发行驶,以每分钟5米的速度向东行驶2分钟,此时,它位于原来位置的哪个方向?相距多远?如何求解?若将时间改成3分钟和4分钟呢?(学生思考、作答)
情境二(略)
(二)新知导学
1.大胆探索,形成规律
回想在情境二的式子中,该如何计算其结果呢?
探究一:引导学生用加法运算:
探究二:比较下面两组算式中左边的因数有什么不同,右边得到的积又有什么不同?从中发现什么规律?并用语言表述.
让学生充分讨论,自己探索,抽取学生发表见解,得出如下结论:
两数相乘,把一因数换成它的相反数,所得的积是原来积的相反数.
试一试(略)
2.探讨规律,导出法则
探究三:
(1) (2)
同
号
(3)
异 (4)
5) 5 × 0 = 0 (-5)× 0 = 0
① 引导学生比较(2)与(4),(3)与(4)中的因数符号有何改变,与此同时积的符号如何变化?加深知识的巩固,突破“两个负数之积是正数”这一难点.
② 引导学生观察、比较(1)和(4)组,(2)和(3)组算式中,两个因数的符号有何特征,积的符号怎样? 得出有理数相乘的符号法则:同号得正,异号得负.
③ 引导学生观察积的绝对值与乘法算式中每个因数的绝对值的积有什么关系?从中发现什么规律?
④ 特别地,当其中一个因数为0时,情况怎样?
让学生逐步探究,分组讨论,鼓励学生说出自己的不同想法,相互交流、补充,并引导学生概括得出:
法则:两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘得0.
3. 理解法则,掌握实质(略)
(三)应用法则,知识迁移
例1 计算:
(1)小题由学生完成,(2) 小题由教师示范 .
(1)(-5)×(-6); (2)(-)×
变式训练
计算: (1) 1 ×(-); (2) (-0.3)×(-1).
(四)快乐套餐
1.突破基础层:
(I) 确定下列乘积的符号.(抢答)(略)
(II) 计算:(接力赛) (略)
2.突破能力层:
计算:(略)
想一想,从计算结果中,你发现有何规律?
填空:若 a 为任意有理数,则: a × 1 =___; a ×(-1)=____.
(五)师生互动、合作交流
教师说明要求, 围绕今天所学内容, 让同桌学生相互出题,给对方计算,不能超出范围.
(六)点金帚(归纳小结)
1. 法则:两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘得0.
2 . 步骤:(1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值.
3. 关键:确定积的符号 同号得正,异号得负.
(七)作业
(学有余力的学生全做,其余学生不做补充.)P52 练习 1、2 ; P57 习题 1、2 .
补充:
1. 沉思阁:
(1) 若 ab < 0, b > 0, 则 a 0. (填“<” “=” “>”).
(2) 若 ab > 0, 则 a、b 满足条件 .
(3)选择:有理数a、b在数轴上位置如图: a 0 b
下列各式正确的是( )
A. a+b > 0 B. b-a < 0 C. ab < 0 D. | b | > | a |
2. 课后拓展:
观察下列各式,它们的积是正是负?
(1)(-2)×(+3)×(+4)×(+5);
(2)(-2)×(-3)×(+4)×(+5);
(3)(-2)×(-3)×(-4)×(+5);
(4)(-2)×(-3)×(-4)×(-5).
3. 课后思考(一):
(-1)×(-1)×…×(-1)+(-1)×(-1)×…×(-1)
2003个(-1) 2004个(-1)
如何计算呢?
课后思考(二)(略)
五、设计思路
本节教学围绕“层层设问→自主探索→发现规律→归纳运用”这一主线展开,对教材内容进行了优化组合,体现了知识的来龙去脉,思路清晰、流畅.在教与学的过程中,创设情境,设置探究问题,学生自主探索、交流合作,而发现规律,进而归纳运用. 充分调动学生自主学习、自主探索的积极性,让学生学会学习、学会探索、学会创新,体现了学生的主体作用. 进而充分体现学生是学习的主人,教师是主导这一教育理念的引路人. 同时,关注学生个性品质的发展培养,及情感态度的发挥. 从而培养学生的团结协作精神,竞争意识,融知识教学和能力培养于一体. 较好的体现了现代教育理念,实施素质教育.因此,学生能理解法则及运用法则.
板书设计
2.9 有理数的乘法(1)
情境 HYPERLINK "http://www.1230.org" 一: 一只玩具小汽车沿东方 小结: 例题
向的路线,从o点出发以每分钟 例1 计算:
5米的速度向东行驶2分钟,此时, 法则: (1)(-5)×(-6); (2)(-)× .
它位于原来位置的哪个方向?相距 两数相乘,同号得正,异号得负, 解:原式 = +(5×6) 解:原式 = -(×)
多远?若将时间改为3、4分钟呢? 并把绝对值相乘; = +30 = -
情境二: 任何数与零相乘,都得零. 变式训练
比较: 计算: (1) 1×(-); (2)(-0.3)×(-1).
步骤:(1)先确定积的符号;
(2)再确定积的绝对值. 巩固与反馈:1、2、3 .
结论:两数相乘,把一个因数换成
它的相反数,所得的积是原来积的 关键:确定积的符号 同号得正, 作业:P52 练习1、2; P57 习题 1、2 .
相反数. 异号得负. 补充: 1 、2、3 .
(-5)×2 = -10
(-5)×3 = -15
(-5)×4 = -20
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
(-5)× 2 = -10
(-5)× 3 = -15
(-5)× 4 = -20
5 ×(-2)= -10
5 ×(-3)= -15
5 ×(-4)= -20
(-5)×(-2)= 10
(-5)×(-3)= 15
(-5)×(-4)= 20
(-5)×2=-10
(-5)×3=-15
(-5)×4=-20
5×3=15
5×4=20
本节课大家学得很认真,效果一定不错,想试一试吗?
前面做得很好,继续努力,一定行!
5 × 2 =10
5 × 3 =15
5 × 4 =20
(-5)× 2 = - 1 0
(-5)× 3 = - 1 5
(-5)× 4 = - 2 0
PAGE
4
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
