2021-2022学年高一上学期数学人教A版(2019)必修第一册5.3诱导公式(第二课时)课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.3诱导公式(第二课时)课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 17:26:56 | ||
图片预览






文档简介
(共21张PPT)
第5章 三角函数
5.3 诱导公式
(第二课时)
1.在诱导公式二~四的基础上,掌握诱导公式五~六的推导.
2.能够利用诱导公式解决简单的求值、化简与证明问题.
课标要求
通过诱导公式的推导及应用,逐步培养学生的数学抽象、逻辑推理和数学运算素养.
教学目标
素养要求
锐角的
三角函数
0~2π的角
的三角函数
任意正角的
三角函数
任意负角的
三角函数
【利用诱导公式一~四把任意角的三角函数转化成锐角的三角函数的步骤】
用公式一或公式三
用公式二或公式四
用公式一
公式四: sin(π-α)=sinα; cos(π-α)=-cosα; tan(π-α)=-tanα.
公式三: sin(-α)=-sinα; cos(-α)= cosα; tan(-α)=-tanα.
公式二: sin(π+α)=-sinα; cos(π+α)= -cosα; tan(π+α)=tanα.
公式一: sin(2kπ+α)=sinα; cos(2kπ+α)=cosα; tan(2kπ+α)=tanα.
复习引入
探究:
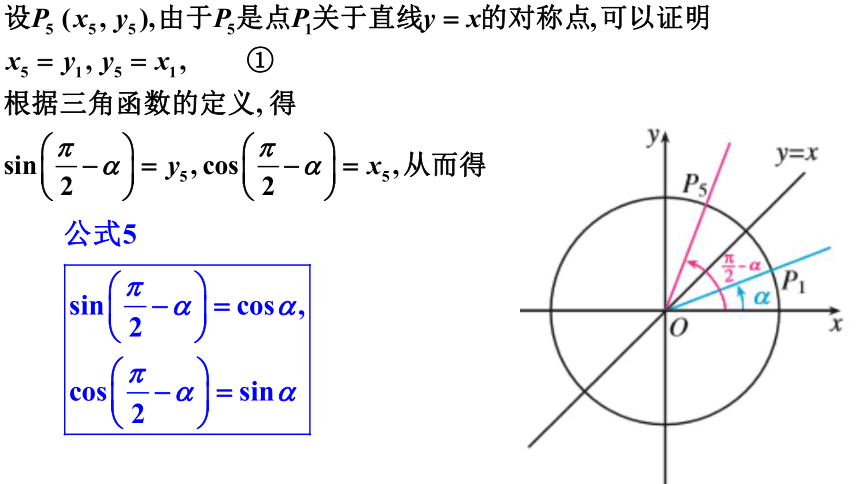
利用公式五或公式六,可以实现正弦函数与余弦函数的相互转化.公式一~公式六都叫做诱导公式
探究:
cos α
sin α
-sin α
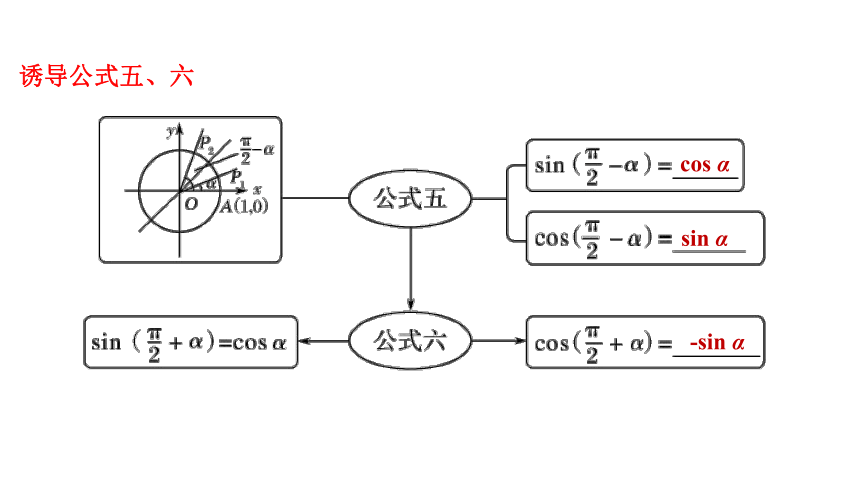
诱导公式五、六
诱导公式五~六
【总结1】公式五和公式六可以概括如下:
的正弦(余弦)函数值,分别等于角α的余弦(正弦)函数值,前面
加上一个把α看成锐角时原函数值的符号.简记为:“函数名改变,符号看象限”
【总结2】六组诱导公式各有什么用?
公式一:将任意角转化成0~2π之间的角求值
公式二:将0~2π之间的角转化成0~π之间的角求值
公式三:将负角转化成正角求值
公式四:将 之间的角转化成 之间的角求值
公式五、六:实现正弦和余弦之间的相互转化
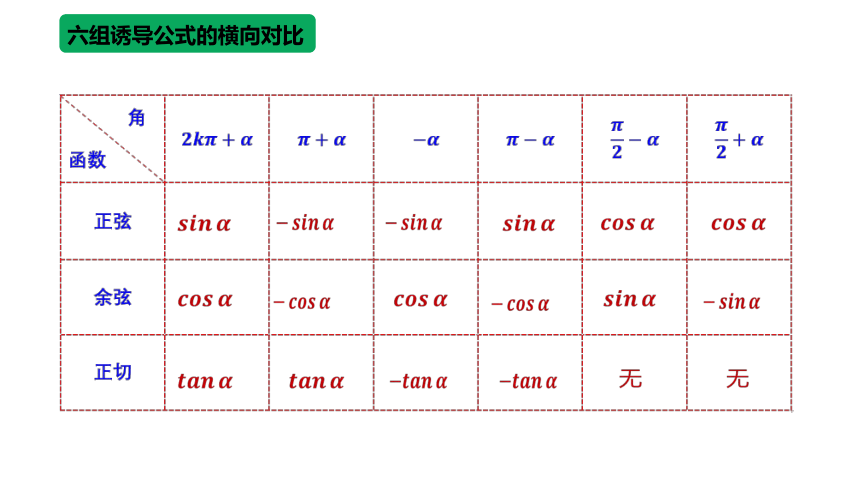
六组诱导公式的横向对比
诱导公式总结:
口诀:奇变偶不变,符号看象限
意义:
例题分析:
利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其中特别注意函数名称和符号的确定.其步骤:去负—脱周—化锐,即
思维升华:
课堂练习:
C
A
解析 cos 64.7°=cos (90°-25.3°)=sin 25.3°=a,故选A.
44.5
4.cos21°+cos22°+cos23°+…+cos289°=________.
解析 cos21°+cos22°+cos23°+…+cos289°
=cos21°+cos22°+cos23°+…+sin21°
课堂小结:
分层训练
第5章 三角函数
5.3 诱导公式
(第二课时)
1.在诱导公式二~四的基础上,掌握诱导公式五~六的推导.
2.能够利用诱导公式解决简单的求值、化简与证明问题.
课标要求
通过诱导公式的推导及应用,逐步培养学生的数学抽象、逻辑推理和数学运算素养.
教学目标
素养要求
锐角的
三角函数
0~2π的角
的三角函数
任意正角的
三角函数
任意负角的
三角函数
【利用诱导公式一~四把任意角的三角函数转化成锐角的三角函数的步骤】
用公式一或公式三
用公式二或公式四
用公式一
公式四: sin(π-α)=sinα; cos(π-α)=-cosα; tan(π-α)=-tanα.
公式三: sin(-α)=-sinα; cos(-α)= cosα; tan(-α)=-tanα.
公式二: sin(π+α)=-sinα; cos(π+α)= -cosα; tan(π+α)=tanα.
公式一: sin(2kπ+α)=sinα; cos(2kπ+α)=cosα; tan(2kπ+α)=tanα.
复习引入
探究:
利用公式五或公式六,可以实现正弦函数与余弦函数的相互转化.公式一~公式六都叫做诱导公式
探究:
cos α
sin α
-sin α
诱导公式五、六
诱导公式五~六
【总结1】公式五和公式六可以概括如下:
的正弦(余弦)函数值,分别等于角α的余弦(正弦)函数值,前面
加上一个把α看成锐角时原函数值的符号.简记为:“函数名改变,符号看象限”
【总结2】六组诱导公式各有什么用?
公式一:将任意角转化成0~2π之间的角求值
公式二:将0~2π之间的角转化成0~π之间的角求值
公式三:将负角转化成正角求值
公式四:将 之间的角转化成 之间的角求值
公式五、六:实现正弦和余弦之间的相互转化
六组诱导公式的横向对比
诱导公式总结:
口诀:奇变偶不变,符号看象限
意义:
例题分析:
利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其中特别注意函数名称和符号的确定.其步骤:去负—脱周—化锐,即
思维升华:
课堂练习:
C
A
解析 cos 64.7°=cos (90°-25.3°)=sin 25.3°=a,故选A.
44.5
4.cos21°+cos22°+cos23°+…+cos289°=________.
解析 cos21°+cos22°+cos23°+…+cos289°
=cos21°+cos22°+cos23°+…+sin21°
课堂小结:
分层训练
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
