2021-2022学年高一数学人教A版(2019)必修一5.2.1三角函数的概念课件(27张ppt)
文档属性
| 名称 | 2021-2022学年高一数学人教A版(2019)必修一5.2.1三角函数的概念课件(27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
5.2.1 三角函数的概念
复习回顾
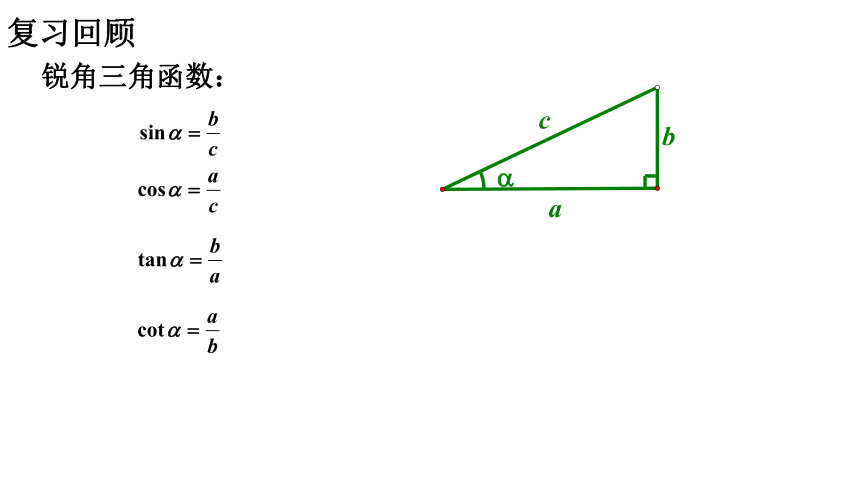
锐角三角函数:
c
b
a
a
x
y
o
r
P(a,b)
M
a
设α是一个锐角,P(a,b)是其终边上任意一点,记r= ,那么:
在终边上移动点P的位置,这三个比值会改变吗
不会,与P点在终边上的位置无关
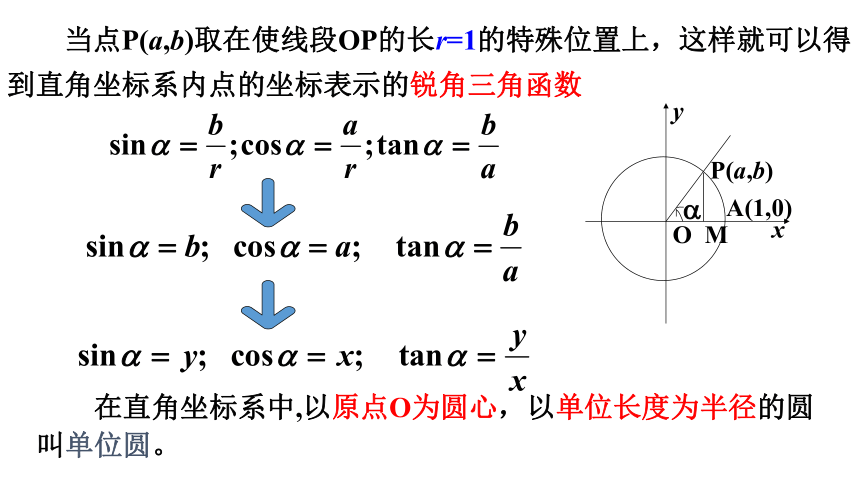
当点P(a,b)取在使线段OP的长r=1的特殊位置上,这样就可以得到直角坐标系内点的坐标表示的锐角三角函数
x
A(1,0)
y
O
P(a,b)
a
M
在直角坐标系中,以原点O为圆心,以单位长度为半径的圆叫单位圆。
类比锐角三角函数,我们也可以利用单位圆定义任意角三角函数(正弦,余弦,正切)。
推广:
任意角的三角函数定义:
x
y
O
P(x,y)
a
A(1,0)
如图,设α是一个任意角(α∈R),它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦函数,记作sinα,即y=sinα;
(2)x叫做α的余弦函数,记作cosα,即x=cosα;
(3) 叫做α的正切函数,记作tanα,即
当角 时,a的终边在y轴上,点 P的横坐标x等于0,所以 无意义,除此之外,对于确定的角以上三个值都是唯一确定的.
我们将正弦函数、余弦函数、正切函数统称为三角函数,通常将它们记为:
【总结】三角函数可以看成是以实数α(α为弧度)为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
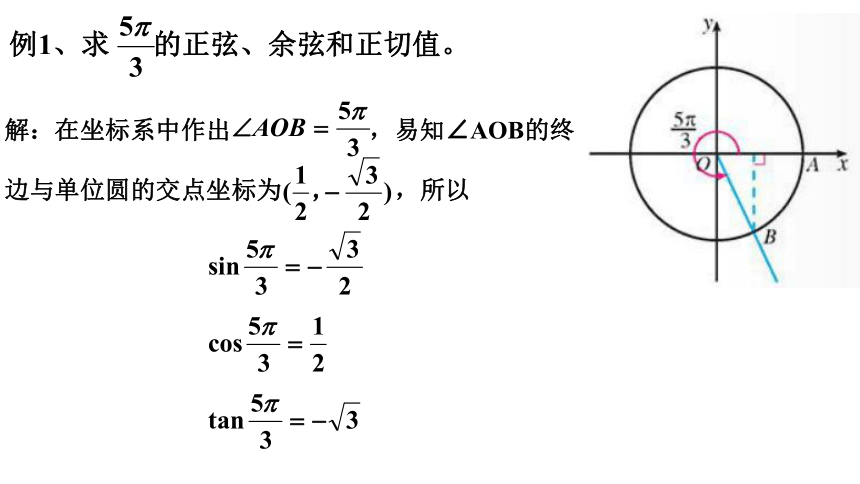
例1、求 的正弦、余弦和正切值。
解:在坐标系中作出 ,易知∠AOB的终边与单位圆的交点坐标为 ,所以
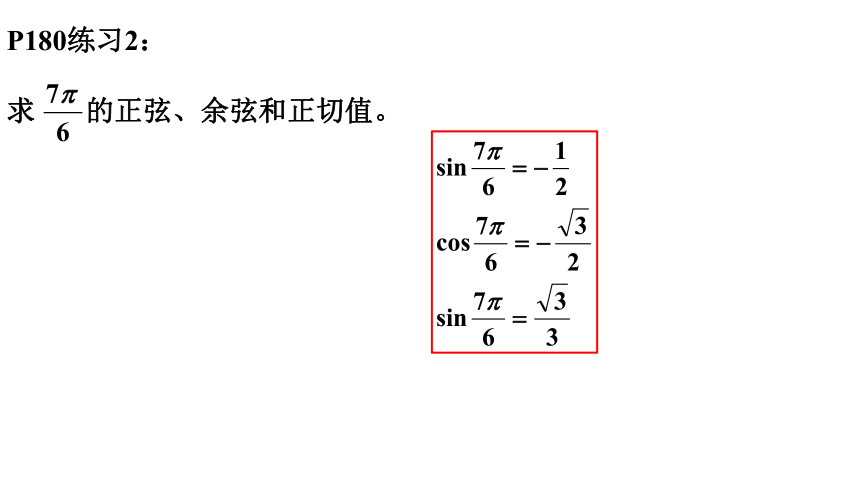
求 的正弦、余弦和正切值。
P180练习2:
例2、如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)坐标为(x,y),点P与原点的距离为r,求证:
如图,设α是一个任意角,P(x,y)是α终边上任意一点,点P与原点的距离为 ,则
例3、已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值。
x
y
O
α
P0(-3,-4)
P180练习3:已知角θ的终边经过点P(-12,5),求角θ的三角函数值。
任意角的三角函数定义:
x
y
O
P(x,y)
a
A(1,0)
如图,设a是一个任意角,它的终边与单位圆(在直角坐标系中,称以原点O为圆心,以单位长度为半径的圆)交于点P(x,y),那么:
(1)y叫做a的正弦,记作sina,即sina=y;
(2)x叫做a的余弦,记作cosa,
即cosa=x;
(3) 叫做a的正切,记作tana,即
知识点回顾
设角a终边上任意一点P的坐标为(x,y),它
与原点的距离为r,则
3
1、α的终边经过P(-b,4),且 ,则b的值为_______
随堂练习
BD
4、已知点P在半径为2的圆上按顺时方向做匀速运动,角速度为1rad/s,求2s时点P所在的位置.
解:如图,以坐标原点为圆心O,OP所在直线为x轴正方向,建立平面直角坐标系
设2s时点P所在的位置记为Q(x,y).
因为点P在半径为2的圆上按顺时方向做匀速运动,角速度为1rad/s,所以圆心角∠POQ=-2rad.
依题意可得
解得x=2cos2,y=-2sin2
所以2s时,点P在该坐标系中的位置为Q(2cos2,-2sin2)
根据任意角的三角定义,写出三角函数在弧度制下的定义域
三角函数的定义域
函数 定义域
y=sinα
y=cosα
y=tanα
三角函数值的符号问题
y
x
o
( )
( )
( )
( )
y
x
o
( )
( )
( )
( )
y
x
o
( )
( )
( )
( )
填写正弦,余弦,正切,余切值在各象限的符号:
规律:
一全正、二正弦、三正切、四余弦
+
+
+
+
+
+
-
-
-
-
-
-
若角a的终边过点(-3,-2),则( )
A.sina tana>0 B.cosa tana>0
C.sina cosa>0 D.sina>0
C
课堂练习
解:(先证充分性)
因为①式sinθ<0成立,
所以θ角的终边可能位于第三或第四象限,
也可能位于y轴非正半轴上;
因为②式tanθ>0成立,
所以θ角的终边可能位于第一或第三象限;
因为①式②式都成立, 所以θ角的终边只能位于第三象限;
于是, θ为第三象限角
例1、求证:角θ为第三象限角的充要条件为
所以必要性成立,即充要性成立.
(再证明必要性)
因为θ是第三象限角,根据定义有sinθ<0, tanθ>0,
由三角函数的定义可知,终边相同的角的同一三角函数值相等。
公式一:
sin(α+ k·2π)=sinα
cos(α+ k·2π)=cosα
tan(α+ k·2π)=tanα
(k∈Z)
2、α+k·2π, k∈Z表示任意与α终边相同的角。
3、此公式表明求任意角的三角函数值的问题,可以转化为求0~2π(0°~360°)间角的三角函数值的问题。
1、运用公式时, k∈Z不能省略!
说明:
4、说明了角和三角函数值的对应关系是多角对一值的关系:即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对应.
例4、确定下列三角函数值的符号:
练习:P182页第3题
例5、求下列三角函数值:
练习:P182页第5题(2)(3)(4)
D
B
课后练习
1、若sinαtanα>0,则α的终边在( )
A.第一象限 B.第四象限 C.第二或第三象限 D.第一或第四象限
2、下列各三角函数值中,取负值的是( )
A.sin(-660°) B.tan160° C.cos(-740°) D.sin(-420°)cos570°
C
5.2.1 三角函数的概念
复习回顾
锐角三角函数:
c
b
a
a
x
y
o
r
P(a,b)
M
a
设α是一个锐角,P(a,b)是其终边上任意一点,记r= ,那么:
在终边上移动点P的位置,这三个比值会改变吗
不会,与P点在终边上的位置无关
当点P(a,b)取在使线段OP的长r=1的特殊位置上,这样就可以得到直角坐标系内点的坐标表示的锐角三角函数
x
A(1,0)
y
O
P(a,b)
a
M
在直角坐标系中,以原点O为圆心,以单位长度为半径的圆叫单位圆。
类比锐角三角函数,我们也可以利用单位圆定义任意角三角函数(正弦,余弦,正切)。
推广:
任意角的三角函数定义:
x
y
O
P(x,y)
a
A(1,0)
如图,设α是一个任意角(α∈R),它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦函数,记作sinα,即y=sinα;
(2)x叫做α的余弦函数,记作cosα,即x=cosα;
(3) 叫做α的正切函数,记作tanα,即
当角 时,a的终边在y轴上,点 P的横坐标x等于0,所以 无意义,除此之外,对于确定的角以上三个值都是唯一确定的.
我们将正弦函数、余弦函数、正切函数统称为三角函数,通常将它们记为:
【总结】三角函数可以看成是以实数α(α为弧度)为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
例1、求 的正弦、余弦和正切值。
解:在坐标系中作出 ,易知∠AOB的终边与单位圆的交点坐标为 ,所以
求 的正弦、余弦和正切值。
P180练习2:
例2、如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)坐标为(x,y),点P与原点的距离为r,求证:
如图,设α是一个任意角,P(x,y)是α终边上任意一点,点P与原点的距离为 ,则
例3、已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值。
x
y
O
α
P0(-3,-4)
P180练习3:已知角θ的终边经过点P(-12,5),求角θ的三角函数值。
任意角的三角函数定义:
x
y
O
P(x,y)
a
A(1,0)
如图,设a是一个任意角,它的终边与单位圆(在直角坐标系中,称以原点O为圆心,以单位长度为半径的圆)交于点P(x,y),那么:
(1)y叫做a的正弦,记作sina,即sina=y;
(2)x叫做a的余弦,记作cosa,
即cosa=x;
(3) 叫做a的正切,记作tana,即
知识点回顾
设角a终边上任意一点P的坐标为(x,y),它
与原点的距离为r,则
3
1、α的终边经过P(-b,4),且 ,则b的值为_______
随堂练习
BD
4、已知点P在半径为2的圆上按顺时方向做匀速运动,角速度为1rad/s,求2s时点P所在的位置.
解:如图,以坐标原点为圆心O,OP所在直线为x轴正方向,建立平面直角坐标系
设2s时点P所在的位置记为Q(x,y).
因为点P在半径为2的圆上按顺时方向做匀速运动,角速度为1rad/s,所以圆心角∠POQ=-2rad.
依题意可得
解得x=2cos2,y=-2sin2
所以2s时,点P在该坐标系中的位置为Q(2cos2,-2sin2)
根据任意角的三角定义,写出三角函数在弧度制下的定义域
三角函数的定义域
函数 定义域
y=sinα
y=cosα
y=tanα
三角函数值的符号问题
y
x
o
( )
( )
( )
( )
y
x
o
( )
( )
( )
( )
y
x
o
( )
( )
( )
( )
填写正弦,余弦,正切,余切值在各象限的符号:
规律:
一全正、二正弦、三正切、四余弦
+
+
+
+
+
+
-
-
-
-
-
-
若角a的终边过点(-3,-2),则( )
A.sina tana>0 B.cosa tana>0
C.sina cosa>0 D.sina>0
C
课堂练习
解:(先证充分性)
因为①式sinθ<0成立,
所以θ角的终边可能位于第三或第四象限,
也可能位于y轴非正半轴上;
因为②式tanθ>0成立,
所以θ角的终边可能位于第一或第三象限;
因为①式②式都成立, 所以θ角的终边只能位于第三象限;
于是, θ为第三象限角
例1、求证:角θ为第三象限角的充要条件为
所以必要性成立,即充要性成立.
(再证明必要性)
因为θ是第三象限角,根据定义有sinθ<0, tanθ>0,
由三角函数的定义可知,终边相同的角的同一三角函数值相等。
公式一:
sin(α+ k·2π)=sinα
cos(α+ k·2π)=cosα
tan(α+ k·2π)=tanα
(k∈Z)
2、α+k·2π, k∈Z表示任意与α终边相同的角。
3、此公式表明求任意角的三角函数值的问题,可以转化为求0~2π(0°~360°)间角的三角函数值的问题。
1、运用公式时, k∈Z不能省略!
说明:
4、说明了角和三角函数值的对应关系是多角对一值的关系:即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对应.
例4、确定下列三角函数值的符号:
练习:P182页第3题
例5、求下列三角函数值:
练习:P182页第5题(2)(3)(4)
D
B
课后练习
1、若sinαtanα>0,则α的终边在( )
A.第一象限 B.第四象限 C.第二或第三象限 D.第一或第四象限
2、下列各三角函数值中,取负值的是( )
A.sin(-660°) B.tan160° C.cos(-740°) D.sin(-420°)cos570°
C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
