人教高中数学必修三3.2.1-古典概型 课件(23张ppt)
文档属性
| 名称 | 人教高中数学必修三3.2.1-古典概型 课件(23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
必修三
1.了解基本事件的特征;
2.掌握古典概率模型的特点;掌握列举法.(重点)
3.学会判断一个试验是否是古典概型,学会用列举法列举基本事件数.(重点、难点).
学习目标
现有一张《霍比特人3》的电影票,小志和小熊熊两人都想要.为了公平起见,他们约定规则:两人同时各抛一枚质地均匀的骰子,点数之和为5就给小志,点数之和为6就给小熊熊.请问这个规则公平合理吗?
问题情境
(2)掷一颗均匀的骰子一次,
(1)掷一枚质地均匀的硬币一次;
正面朝上
反面朝上
1.基本事件
预习反馈
在一次试验中,可能出现的
每一个基本结果称为基本事件.
这两个实验中,可能的结果有哪些?
考查两个实验:
问题1:基本事件有什么特点?
①任何两个基本事件是互斥的.
②任何事件都可以表示成基本事件的和.
(除不可能事件)
总结提升
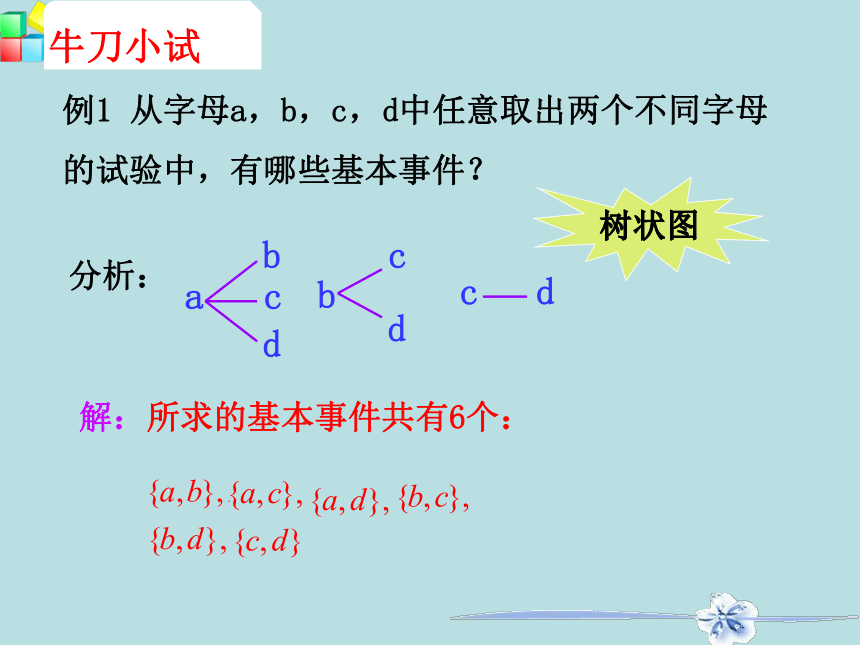
例1 从字母a,b,c,d中任意取出两个不同字母的试验中,有哪些基本事件?
a
b
c
d
b
c
d
c
d
解:所求的基本事件共有6个:
分析:
牛刀小试
问题2:观察对比找出抛硬币、掷骰子试验的共同特征.
抛 基本事件 基本事件出现的可能性
硬币 正面向上
反面向上
骰子 1点、2点、3点、
4点、5点、6点
(1)试验中所有可能出现的基本事件
只有有限个;
(2)每个基本事件出现的可能性
相等.
每个基本事件的概率都
是1/2
每个基本事件的概率都
是1/6
新课探究1
2.我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型.
(1)向一个圆面内随机地投射一个点,如果
该点落在圆内任意一点都是等可能的,你认为
这是古典概型吗 为什么?
不是古典概型.
试试看:请举一个古典概型的例子.
“等可能性”
“有限性”
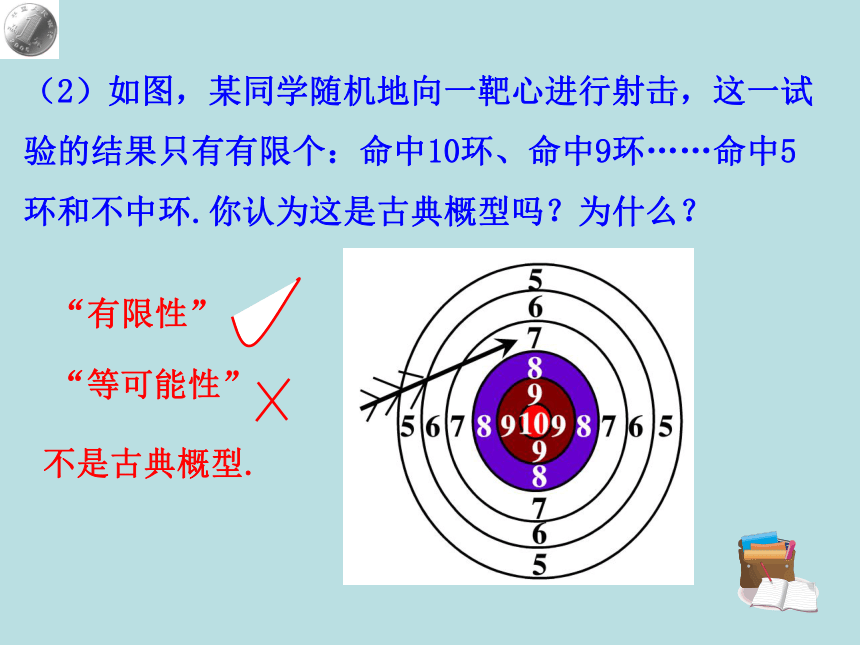
(2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么?
不是古典概型.
“等可能性”
“有限性”
问题3:在古典概型下,如何求随机事件出现的概率?
探讨:基本事件总数为
如:掷一颗均匀的骰子一次,事件A为“出现偶数点”,请问事件A的概率是多少?
6: 1点、2点、3点、4点、5点、6点
事件A包含 个基本事件:2点、4点、6点
3
P(A)=P(2点)+P(4点)+P(6点)
新课探究2
3.对于古典概型,任何事件的概率计算公式为:
注:若一个古典概型有n个基本事件,则每个基本事件发生的概率是
在使用古典概型的概率公式时,
要先判断所求概率模型是不是古典概型.
总结提升
例2 单选题是考试常用的题型,一般是从A, B,C,D四个选项中选择一个正确答案. 假设有一题我们不会做,随机地选择一个答案,那么答对的概率是多少?
牛刀再试
解:基本事件共有4个.随机地选择一个答案,选择A,B,C,D的可能性是相等的.所以这是一个古典概型,
考试中的不定向选择题是从A,B,C,D四个选项中选出所有正确的答案.同学们可能有一种感觉,如果不知道正确答案,不定向选择题更难猜对,试求不定向选择题猜对的概率.
解:基本事件为(A),(B),(C),(D),
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),(A,B,C),(A,B,D),(A,C,D),(B,C,D),
(A,B,C,D).
答对的概率为
变式探究
例3.同时抛两颗均匀的骰子,求:
(1)有哪些基本事件?
(2)点数之和为5的概率是多少?
牛刀三试
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
9
6
7
8
9
10
7
8
9
10
11
9
10
11
12
两个骰子的点数和
共有36种,和是5的结果有4个.
所以,P(点数和为5)=
学以致用
现有一张《霍比特人3》的电影票,小志和小熊熊两人都想要.为了公平起见,他们约定规则:两人同时各抛一枚质地均匀的骰子,点数之和为5就给小志,点数之和为6就给小熊熊.请问这个规则公平合理吗?
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
9
6
7
8
9
10
7
8
9
10
11
9
10
11
12
两个骰子的点数和
共有36种,和是5的结果有4个,和是6的结果有5个.
P(甲)=
P(乙)=
P(甲)共有21种,和是5的结果有2个.
但此时这21个基本事件是等可能发生的吗?
因此,在抛两个骰子试验中,必须对骰子加标记区分.
不是.
问题4:如果不对骰子加标记区分,会出现什么情况?
大显身手
例4.
解法1:合格的4听分别记为1,2,3,4,不合格的2听分别记作a,b.只要检测的2听中有1听不合格,就表示查出了不合格产品.
1 2 3 4 a b
1 (1,1) (1,2) (1,3) (1,4) (1,a) (1,b)
2 (2,1) (2,2) (2,3) (2,4) (2,a) (2,b)
3 (3,1) (3,2) (3,3) (3,4) (3,a) (3,b)
4 (4,1) (4,2) (4,3) (4,4) (4,a) (4,b)
a (a,1) (a,2) (a,3) (a,4) (a,a) (a,b)
b (b,1) (b,2) (b,3) (b,4) (b,a) (b,b)
第1听
第2听
基本事件共有30个,含有不合格的有18个.
列举法1:列表
依次不放回抽取2听饮料,则(x,y)表示一次抽到的结果.
解法2:合格的4听分别记为1,2,3,4,不合格的2听分别记作a,b.看作一次同时抽2听.
列举法2:树状图
①抽得2听均为不合格:
②抽得2听恰有1听不合格:
③抽得2听都是合格的:
1
2
3
4
1.一枚质地的均匀硬币连掷3次,只有一次出现正面的概率是( )
A
趁热打铁
2.甲、乙、丙三名同学站成一排,甲站在中间的概率
是( )
C
作业反馈
1.知识点:
(1)古典概型的定义和特征:有限性、等可能性.
(2)古典概率公式
2. 数学方法:列举法(树状图、列表格或按某种顺序列举等),做到不重不漏.
必做题:课本P133 习题3.2 A组 1.5.6.
选做题:课本P145 3. 5.
课堂小结
必修三
1.了解基本事件的特征;
2.掌握古典概率模型的特点;掌握列举法.(重点)
3.学会判断一个试验是否是古典概型,学会用列举法列举基本事件数.(重点、难点).
学习目标
现有一张《霍比特人3》的电影票,小志和小熊熊两人都想要.为了公平起见,他们约定规则:两人同时各抛一枚质地均匀的骰子,点数之和为5就给小志,点数之和为6就给小熊熊.请问这个规则公平合理吗?
问题情境
(2)掷一颗均匀的骰子一次,
(1)掷一枚质地均匀的硬币一次;
正面朝上
反面朝上
1.基本事件
预习反馈
在一次试验中,可能出现的
每一个基本结果称为基本事件.
这两个实验中,可能的结果有哪些?
考查两个实验:
问题1:基本事件有什么特点?
①任何两个基本事件是互斥的.
②任何事件都可以表示成基本事件的和.
(除不可能事件)
总结提升
例1 从字母a,b,c,d中任意取出两个不同字母的试验中,有哪些基本事件?
a
b
c
d
b
c
d
c
d
解:所求的基本事件共有6个:
分析:
牛刀小试
问题2:观察对比找出抛硬币、掷骰子试验的共同特征.
抛 基本事件 基本事件出现的可能性
硬币 正面向上
反面向上
骰子 1点、2点、3点、
4点、5点、6点
(1)试验中所有可能出现的基本事件
只有有限个;
(2)每个基本事件出现的可能性
相等.
每个基本事件的概率都
是1/2
每个基本事件的概率都
是1/6
新课探究1
2.我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型.
(1)向一个圆面内随机地投射一个点,如果
该点落在圆内任意一点都是等可能的,你认为
这是古典概型吗 为什么?
不是古典概型.
试试看:请举一个古典概型的例子.
“等可能性”
“有限性”
(2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么?
不是古典概型.
“等可能性”
“有限性”
问题3:在古典概型下,如何求随机事件出现的概率?
探讨:基本事件总数为
如:掷一颗均匀的骰子一次,事件A为“出现偶数点”,请问事件A的概率是多少?
6: 1点、2点、3点、4点、5点、6点
事件A包含 个基本事件:2点、4点、6点
3
P(A)=P(2点)+P(4点)+P(6点)
新课探究2
3.对于古典概型,任何事件的概率计算公式为:
注:若一个古典概型有n个基本事件,则每个基本事件发生的概率是
在使用古典概型的概率公式时,
要先判断所求概率模型是不是古典概型.
总结提升
例2 单选题是考试常用的题型,一般是从A, B,C,D四个选项中选择一个正确答案. 假设有一题我们不会做,随机地选择一个答案,那么答对的概率是多少?
牛刀再试
解:基本事件共有4个.随机地选择一个答案,选择A,B,C,D的可能性是相等的.所以这是一个古典概型,
考试中的不定向选择题是从A,B,C,D四个选项中选出所有正确的答案.同学们可能有一种感觉,如果不知道正确答案,不定向选择题更难猜对,试求不定向选择题猜对的概率.
解:基本事件为(A),(B),(C),(D),
(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),(A,B,C),(A,B,D),(A,C,D),(B,C,D),
(A,B,C,D).
答对的概率为
变式探究
例3.同时抛两颗均匀的骰子,求:
(1)有哪些基本事件?
(2)点数之和为5的概率是多少?
牛刀三试
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
9
6
7
8
9
10
7
8
9
10
11
9
10
11
12
两个骰子的点数和
共有36种,和是5的结果有4个.
所以,P(点数和为5)=
学以致用
现有一张《霍比特人3》的电影票,小志和小熊熊两人都想要.为了公平起见,他们约定规则:两人同时各抛一枚质地均匀的骰子,点数之和为5就给小志,点数之和为6就给小熊熊.请问这个规则公平合理吗?
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
5
6
7
8
9
6
7
8
9
10
7
8
9
10
11
9
10
11
12
两个骰子的点数和
共有36种,和是5的结果有4个,和是6的结果有5个.
P(甲)=
P(乙)=
P(甲)
但此时这21个基本事件是等可能发生的吗?
因此,在抛两个骰子试验中,必须对骰子加标记区分.
不是.
问题4:如果不对骰子加标记区分,会出现什么情况?
大显身手
例4.
解法1:合格的4听分别记为1,2,3,4,不合格的2听分别记作a,b.只要检测的2听中有1听不合格,就表示查出了不合格产品.
1 2 3 4 a b
1 (1,1) (1,2) (1,3) (1,4) (1,a) (1,b)
2 (2,1) (2,2) (2,3) (2,4) (2,a) (2,b)
3 (3,1) (3,2) (3,3) (3,4) (3,a) (3,b)
4 (4,1) (4,2) (4,3) (4,4) (4,a) (4,b)
a (a,1) (a,2) (a,3) (a,4) (a,a) (a,b)
b (b,1) (b,2) (b,3) (b,4) (b,a) (b,b)
第1听
第2听
基本事件共有30个,含有不合格的有18个.
列举法1:列表
依次不放回抽取2听饮料,则(x,y)表示一次抽到的结果.
解法2:合格的4听分别记为1,2,3,4,不合格的2听分别记作a,b.看作一次同时抽2听.
列举法2:树状图
①抽得2听均为不合格:
②抽得2听恰有1听不合格:
③抽得2听都是合格的:
1
2
3
4
1.一枚质地的均匀硬币连掷3次,只有一次出现正面的概率是( )
A
趁热打铁
2.甲、乙、丙三名同学站成一排,甲站在中间的概率
是( )
C
作业反馈
1.知识点:
(1)古典概型的定义和特征:有限性、等可能性.
(2)古典概率公式
2. 数学方法:列举法(树状图、列表格或按某种顺序列举等),做到不重不漏.
必做题:课本P133 习题3.2 A组 1.5.6.
选做题:课本P145 3. 5.
课堂小结
