2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题(第一课时)课件(14张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题(第一课时)课件(14张ppt) | 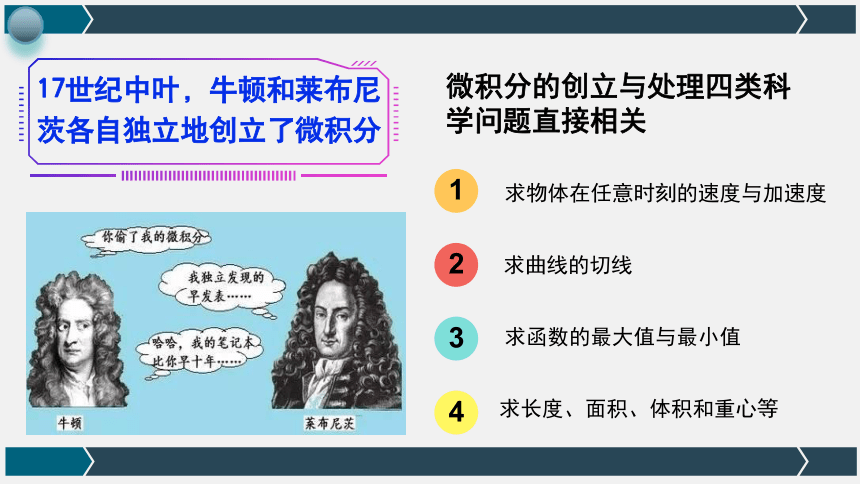 | |
| 格式 | pptx | ||
| 文件大小 | 44.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 19:30:59 | ||
图片预览






文档简介
(共14张PPT)
17世纪中叶,牛顿和莱布尼茨各自独立地创立了微积分
微积分的创立与处理四类科学问题直接相关
1
求物体在任意时刻的速度与加速度
2
求曲线的切线
3
求函数的最大值与最小值
4
求长度、面积、体积和重心等
5.1导数的概念及其意义
5.1.1 变化率问题
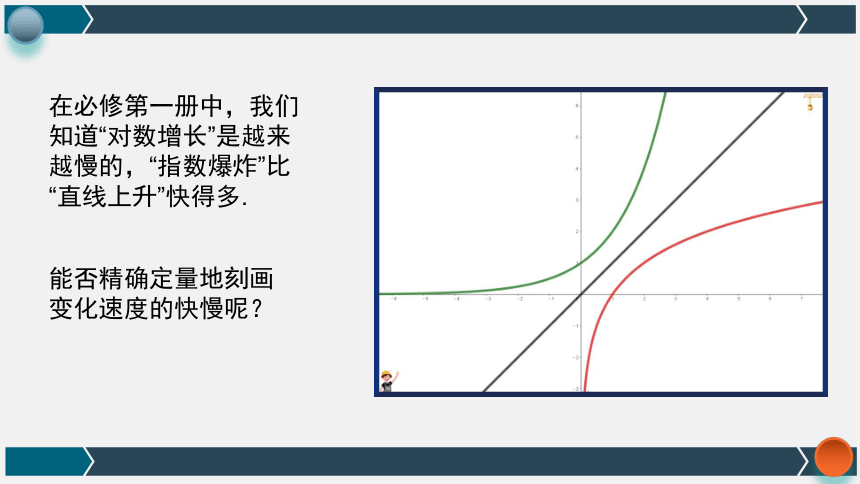
在必修第一册中,我们知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.
能否精确定量地刻画变化速度的快慢呢?
5.1.1变化率问题
问题1 高台跳水运动员的速度
__________
问题1 高台跳水运动员的速度
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如何描述运动员从起跳到如水的过程中运动的快慢程度呢?
问题1 高台跳水运动员的速度
=
=
一般地,
=
=
问题1 高台跳水运动员的速度
=
(1) 运动员在这段时间里是静止的吗
(2) 平均速度能准确反映运动员的运动状态吗
显然,在这段时间内,运动员并不处于静止状态.
因此,用平均速度不能准确反映运动员在这段时间内里的运动状态.
0
问题1 高台跳水运动员的速度
(1)瞬时速度与平均速度有什么关系?
(2)你能利用这种关系求运动员在t=1s时的瞬时速度吗?
瞬时速度:
物体在某一时刻的速度
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念.
问题1 高台跳水运动员的速度
我们在t=1之后或之前,任意取一个时刻1+Δt,Δt是时间改变量,可以是正值,也可以是负值,但不为0
当Δt<0时,在时间段[1+Δt,1]内 当Δt<0时,在时间段[1+Δt,1]内 Δt Δt
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
-0.000001 0.000001
...... ......
-4.951
-4.9951
-4.99951
-4.999951
-4.9999951
-5.049
-5.0049
-5.00049
-5.000049
-5.0000049
问题1 高台跳水运动员的速度
当Δt无限趋近于0时,平均速度有什么变化趋势?
无限趋近于-5
数学中,我们把-5叫做“当Δt无限趋近于0时,的极限”,记为
因此,运动员在t=1时的瞬时速度v(1)=-5m/s.
知识应用
例:(1)求运动员在t=2 s 时的瞬时速度
(2)求运动员在t=0.5 s 时的瞬时速度
(3)求运动员从起跳到入水过程中在某一时刻 t0 的瞬时速度?
知识应用
练习:火箭发射 t s 后,其高度(单位:m)为.求
(1)在1≤t≤2这段时间里,火箭爬高的平均速度;
(2)发射后第10s时,火箭爬高的瞬时速度.
知识应用
课堂小结
1.本节课收获了哪些知识?
2.在获得知识的过程中用到了哪些思想、方法?
平均速度
瞬时速度
特殊到一般、极限思想
17世纪中叶,牛顿和莱布尼茨各自独立地创立了微积分
微积分的创立与处理四类科学问题直接相关
1
求物体在任意时刻的速度与加速度
2
求曲线的切线
3
求函数的最大值与最小值
4
求长度、面积、体积和重心等
5.1导数的概念及其意义
5.1.1 变化率问题
在必修第一册中,我们知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.
能否精确定量地刻画变化速度的快慢呢?
5.1.1变化率问题
问题1 高台跳水运动员的速度
__________
问题1 高台跳水运动员的速度
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如何描述运动员从起跳到如水的过程中运动的快慢程度呢?
问题1 高台跳水运动员的速度
=
=
一般地,
=
=
问题1 高台跳水运动员的速度
=
(1) 运动员在这段时间里是静止的吗
(2) 平均速度能准确反映运动员的运动状态吗
显然,在这段时间内,运动员并不处于静止状态.
因此,用平均速度不能准确反映运动员在这段时间内里的运动状态.
0
问题1 高台跳水运动员的速度
(1)瞬时速度与平均速度有什么关系?
(2)你能利用这种关系求运动员在t=1s时的瞬时速度吗?
瞬时速度:
物体在某一时刻的速度
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念.
问题1 高台跳水运动员的速度
我们在t=1之后或之前,任意取一个时刻1+Δt,Δt是时间改变量,可以是正值,也可以是负值,但不为0
当Δt<0时,在时间段[1+Δt,1]内 当Δt<0时,在时间段[1+Δt,1]内 Δt Δt
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
-0.000001 0.000001
...... ......
-4.951
-4.9951
-4.99951
-4.999951
-4.9999951
-5.049
-5.0049
-5.00049
-5.000049
-5.0000049
问题1 高台跳水运动员的速度
当Δt无限趋近于0时,平均速度有什么变化趋势?
无限趋近于-5
数学中,我们把-5叫做“当Δt无限趋近于0时,的极限”,记为
因此,运动员在t=1时的瞬时速度v(1)=-5m/s.
知识应用
例:(1)求运动员在t=2 s 时的瞬时速度
(2)求运动员在t=0.5 s 时的瞬时速度
(3)求运动员从起跳到入水过程中在某一时刻 t0 的瞬时速度?
知识应用
练习:火箭发射 t s 后,其高度(单位:m)为.求
(1)在1≤t≤2这段时间里,火箭爬高的平均速度;
(2)发射后第10s时,火箭爬高的瞬时速度.
知识应用
课堂小结
1.本节课收获了哪些知识?
2.在获得知识的过程中用到了哪些思想、方法?
平均速度
瞬时速度
特殊到一般、极限思想
