华东师大版数学八年级上册 13.2.5 边边边教案
文档属性
| 名称 | 华东师大版数学八年级上册 13.2.5 边边边教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 84.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览


文档简介
13.2三角形全等的判定(SSS)
教学目标:
1.知识与技能:了解三角形的稳定性,会应用“边边边”判定两个三角形全等.
2.过程与方法:使学生经历探索三角形全等的条件的过程,体验用操作、归纳得出结论的过程。了解探究问题是采用分类的思想,从简单入手。
3.情感、态度与价值观:通过探究三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想、乐于探究的良好品质以及发现问题的能力。
重点和难点
重点:“SSS”定理的探索过程和应用。
难点:“SSS”定理的应用。
课 型:新授课
教学准备:多媒体课件、三角板等
教学方法:引导启发式、合作探究式等
教学过程:
一、 知识回顾
1、什么是全等三角形?
能够完全重合的两个三角形是全等三角形。
2、我们已学过了哪些判定三角形全等的方法? (S.A.S. A.A.S. A.S.A. )
我们已知道如果两个三角形有两边及其夹角分别相等的两个三角形全等;两角及其夹边分别相等的两个三角形全等;两角分别相等且其中一组等角的对边相等的两个三角形全等。
这节课我们继续来探索三角形全等的判定方法。
板书课题--------全等三角形的判定(5)----边边边
二、探究新知
1、观察思考
(1) 如果两个三角形有三个角对应相等,这两个三角形全等吗?为什么?(多媒体展示)
再出示两个等腰直角三角板直观展示。
如果把三个角对应相等改为三条边对应相等,这两个三角形全等吗?
2、边边边定理的探索:
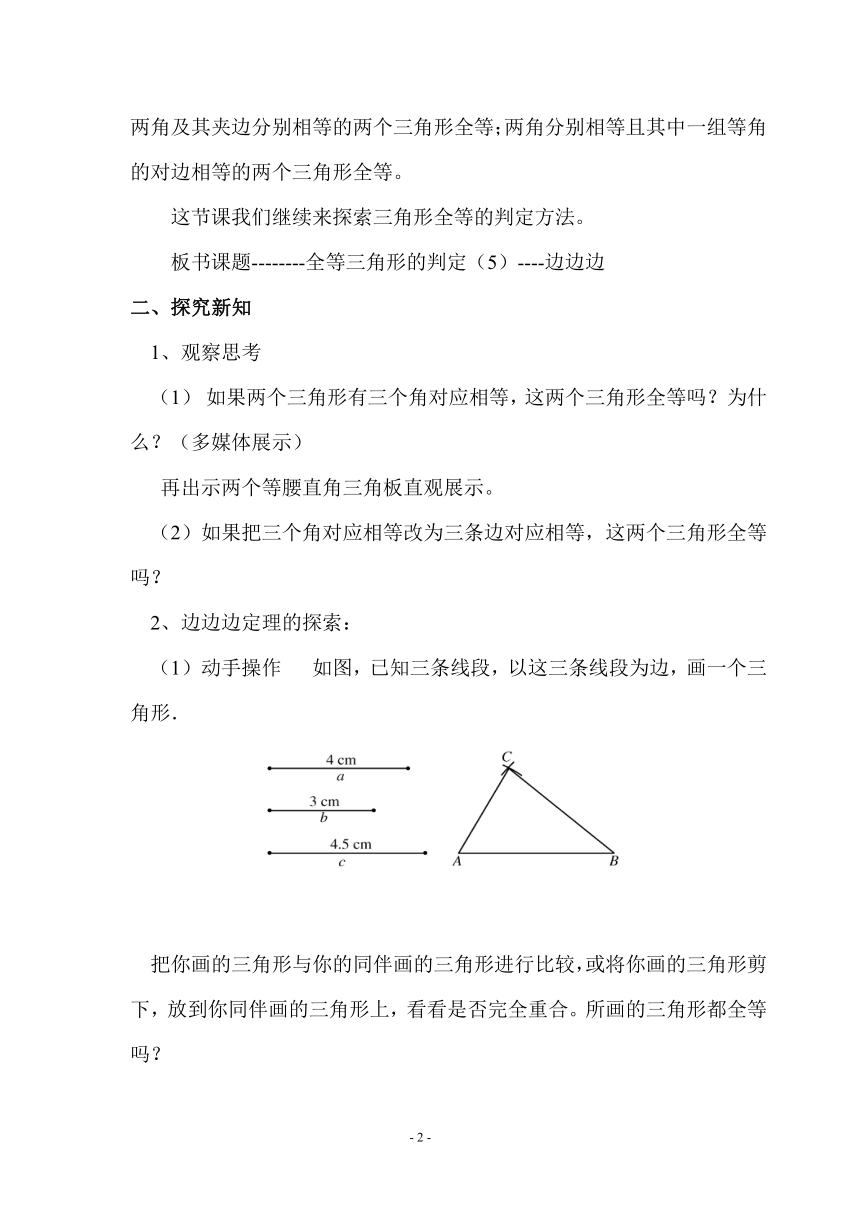
(1)动手操作 如图,已知三条线段,以这三条线段为边,画一个三角形.
把你画的三角形与你的同伴画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合。所画的三角形都全等吗?
换三条线段,试试看,是否有同样的结论?
由以上操作,可以发现它们是完全重合,所画的三角形都全等。(只要三角形的三边长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。)
由此你发现了什么?能得到判定三角形全等的另一种简便方法吗
(2)归纳:
边边边定理:三边分别相等的两个三角形全等(简记为S.S.S. (或边边边)
几何语言:
在△ABC和△DEF中,
∵AB=DE BC=EF AC=DF
∴ △ABC≌△DEF (S.S.S.)
三、新知运用
例 已知:如图,在四边形ABCD中,AB = CD , AD = CB。
求证: ∠A = ∠C
分析: 证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
请一位同学上台试着完成证明过程,然后集体订正。
证明:连结BD,
在△ABD和△CDB中 ,
∵ AB = CD AD =CB(已知),
BD=DB(公共边),
∴ △ABD≌△CDB(S.S.S.)
∴ ∠A = ∠C (全等三角形的对应角相等)。
强调对应点写在对应位置上,使学生养成良好的数学思维与书写习惯.
四 、巩固提升
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO
与△DCO
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
五、归纳小结
1、两个三角形全等的判定方法
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
(强调:判定三角形全等至少有一组边)
2、学生谈本节课的收获:
(1)请说出目前判定三角形全等的4种方法:
(S.A.S. A.S.A. A.A.S. S.S.S. )
(2)“边边边”在应用中用到的数学方法:
证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
六、作业
课堂作业:第73页习题2 第76页3、4题
拓展作业:
1、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:
⑴∠D=∠B;
⑵AE∥CF.
七、教学反思
贴近生活,让学生在体验中感悟学习.动手操作,让学生在活动中探究学习.开放课堂,让学生在互动中创新学习.学生对于数学语言的使用是一个系统与漫长的过程,要加强训练。
- 4 -
教学目标:
1.知识与技能:了解三角形的稳定性,会应用“边边边”判定两个三角形全等.
2.过程与方法:使学生经历探索三角形全等的条件的过程,体验用操作、归纳得出结论的过程。了解探究问题是采用分类的思想,从简单入手。
3.情感、态度与价值观:通过探究三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想、乐于探究的良好品质以及发现问题的能力。
重点和难点
重点:“SSS”定理的探索过程和应用。
难点:“SSS”定理的应用。
课 型:新授课
教学准备:多媒体课件、三角板等
教学方法:引导启发式、合作探究式等
教学过程:
一、 知识回顾
1、什么是全等三角形?
能够完全重合的两个三角形是全等三角形。
2、我们已学过了哪些判定三角形全等的方法? (S.A.S. A.A.S. A.S.A. )
我们已知道如果两个三角形有两边及其夹角分别相等的两个三角形全等;两角及其夹边分别相等的两个三角形全等;两角分别相等且其中一组等角的对边相等的两个三角形全等。
这节课我们继续来探索三角形全等的判定方法。
板书课题--------全等三角形的判定(5)----边边边
二、探究新知
1、观察思考
(1) 如果两个三角形有三个角对应相等,这两个三角形全等吗?为什么?(多媒体展示)
再出示两个等腰直角三角板直观展示。
如果把三个角对应相等改为三条边对应相等,这两个三角形全等吗?
2、边边边定理的探索:
(1)动手操作 如图,已知三条线段,以这三条线段为边,画一个三角形.
把你画的三角形与你的同伴画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合。所画的三角形都全等吗?
换三条线段,试试看,是否有同样的结论?
由以上操作,可以发现它们是完全重合,所画的三角形都全等。(只要三角形的三边长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。)
由此你发现了什么?能得到判定三角形全等的另一种简便方法吗
(2)归纳:
边边边定理:三边分别相等的两个三角形全等(简记为S.S.S. (或边边边)
几何语言:
在△ABC和△DEF中,
∵AB=DE BC=EF AC=DF
∴ △ABC≌△DEF (S.S.S.)
三、新知运用
例 已知:如图,在四边形ABCD中,AB = CD , AD = CB。
求证: ∠A = ∠C
分析: 证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
连结BD后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
请一位同学上台试着完成证明过程,然后集体订正。
证明:连结BD,
在△ABD和△CDB中 ,
∵ AB = CD AD =CB(已知),
BD=DB(公共边),
∴ △ABD≌△CDB(S.S.S.)
∴ ∠A = ∠C (全等三角形的对应角相等)。
强调对应点写在对应位置上,使学生养成良好的数学思维与书写习惯.
四 、巩固提升
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO
与△DCO
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?
五、归纳小结
1、两个三角形全等的判定方法
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
(强调:判定三角形全等至少有一组边)
2、学生谈本节课的收获:
(1)请说出目前判定三角形全等的4种方法:
(S.A.S. A.S.A. A.A.S. S.S.S. )
(2)“边边边”在应用中用到的数学方法:
证明线段(或角)相等转化为证明线段(或角)所在的两个三角形全等
六、作业
课堂作业:第73页习题2 第76页3、4题
拓展作业:
1、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:
⑴∠D=∠B;
⑵AE∥CF.
七、教学反思
贴近生活,让学生在体验中感悟学习.动手操作,让学生在活动中探究学习.开放课堂,让学生在互动中创新学习.学生对于数学语言的使用是一个系统与漫长的过程,要加强训练。
- 4 -
