北师大版数学七下第一章整式的乘除回顾与思考课件(共31张PPT)
文档属性
| 名称 | 北师大版数学七下第一章整式的乘除回顾与思考课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 571.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 20:44:00 | ||
图片预览

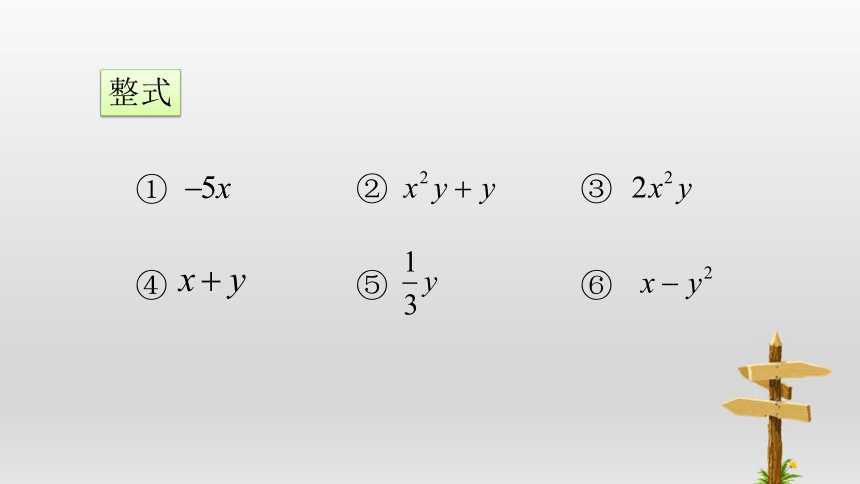





文档简介
(共31张PPT)
回顾与思考
北师大版初中数学七年级下册
第一章 整式的乘除
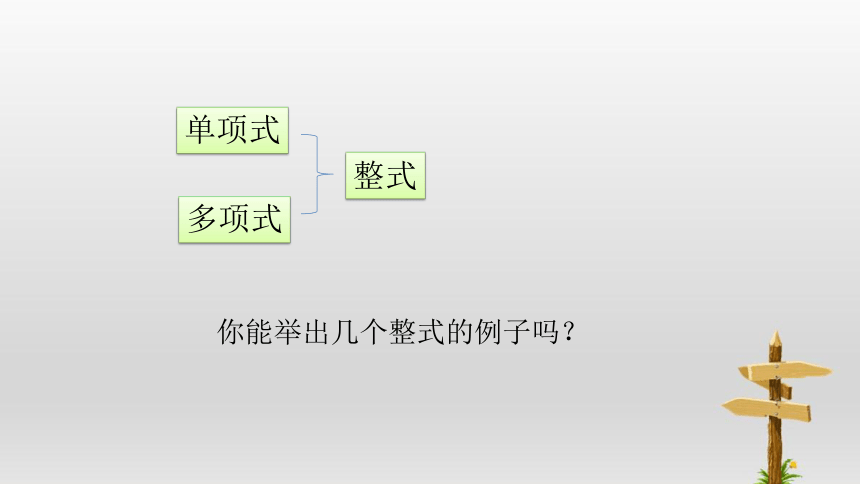
单项式
多项式
整式
你能举出几个整式的例子吗?
整式
①
②
③
④
⑤
⑥
①
②
③
④
⑤
⑥
整式的运算
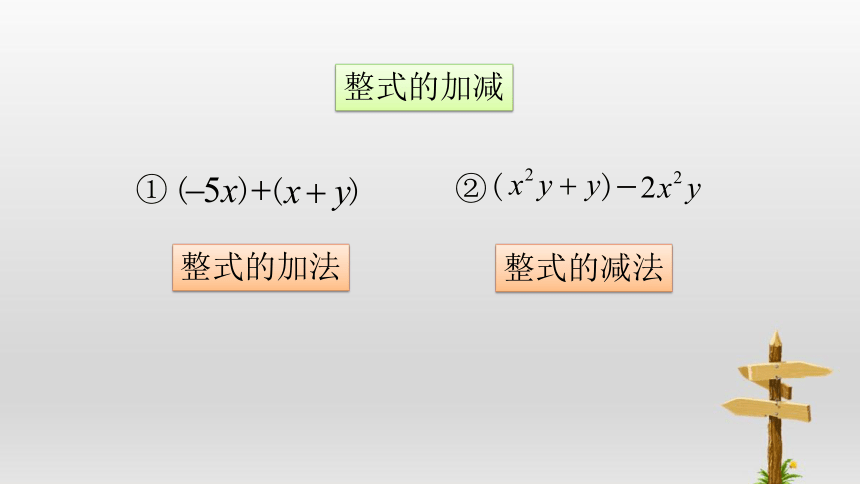
你能根据上面的整式写出几个整式有关运算的式子吗?
①
②
( )
( )
( )
整式的加法
整式的减法
整式的加减
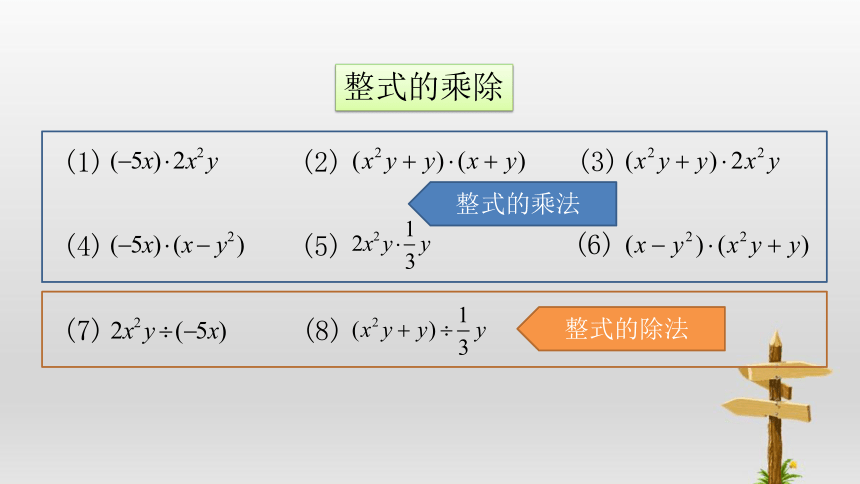
整式的乘除
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
整式的乘法
整式的除法
整式的乘法
(1)
(2)
(3)
(4)
(5)
(6)
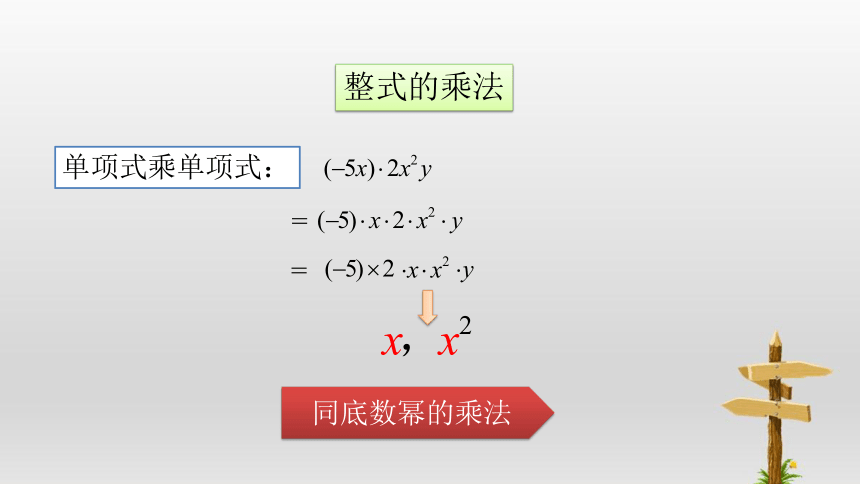
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
整式的乘法
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
(1)
(5)
(3)
(4)
(2)
(6)
整式的乘法
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
(1)
(5)
(3)
(4)
(2)
(6)
整式的乘法
单项式乘单项式:
=
=
同底数幂的乘法
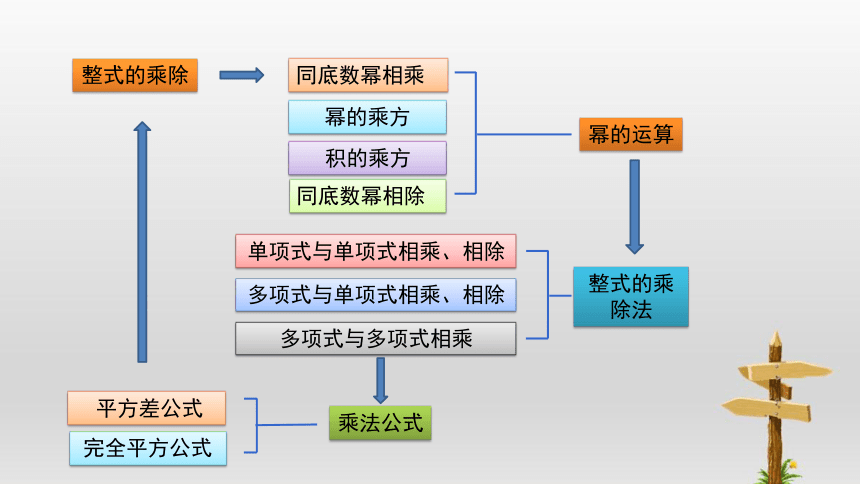
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
单项式与单项式相乘、相除
多项式与多项式相乘
幂的运算
同底数幂相乘
幂的乘方
同底数幂相除
整式的乘除法
乘法公式
知识建构
快速判断以下各题是否正确。
×
√
×
×
×
×
×
×
√
√
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
要点梳理
法则名称 文字表示 式子表示
同底数幂的乘法 同底数幂相乘, 底数 ,指数 . am an= (m、n为正整数)
幂的乘方 幂的乘方, 底数 ,指数 . (am)n= (m、n为正整数)
积的乘方 积的乘方,等于把积的每个因式分别 ,再把所得的幂 . (ab)n= (n为正整数)
am+n
amn
anbn
不变
相乘
相加
不变
相乘
乘方
[注意]
(1)其中的a、b可以 是单独的数、单独的字母,还可以是一个任意的代数式;
(2)这几个法则容易混淆,计算时必须先搞清楚该不该用法则、该用哪个法则.
要点梳理
同底数幂的除法
(1)同底数幂相除, 底数不变,指数相减.
(a≠0, m、n为任意整数)
(2)任何不等于零的数的零次幂都等于1.
(3)负整数指数幂:
(a≠0,n为正整数)
考点讲练
考点一 幂的乘法运算
例1 计算:
(1)(2a)3(b3)2 ·4a3b4; (2)(-8)2021 ×(0.125)2020.
解:(1)原式=8a3b6 ×4a3b4=32a3+3b6+4=2a6b10.
(2)原式=(-8)×(-8)2020 ×(0.125)2020
=(-8)[(-8) ×0.125]2020
=(-8)×(-1)2020=-8.
方法总结
幂的乘法运算包括同底数幂的乘法、幂的乘方、积的乘方.这三种运算性质贯穿全章,是整式乘法的基础.其逆向运用可将问题化繁为简,负数乘方结果的符号,奇次方得负,偶次方得正.
转化思想
转化思想将要解决的问题转化为另一个较易解决的问题,这是初中数学中常用的思想方法.如本章中,多项式×多项式 单项式×多项式 单项式×单项式 有理数的乘法和同底数幂的乘法.
考点讲练
考点一 幂的乘法运算
方法总结
考点讲练
考点一 幂的乘法运算
1.(2019·深圳)下列运算正确的是( )
A. a2 + a2 =a4 B. a3 · a4 =a12
C. (a3) 4=a12 D. (ab) 2=ab2
C
针对训练
解:∵420=(42)10=1610,
∴1610>1510,
∴420>1510.
2. 比较大小:420与1510.
转化思想
考点讲练
3. 若2a+5b-3=0,则4a·32b= .
【解析】已知条件是2a+5b-3=0,无法求出a,b的值. 因此可以逆用积的乘方先把4a·32b.化简为含有与已知条件相关的部分,即4a·32b=22a·25b=22a+5b.把2a+5b看做一个整体,因为2a+5b-3=0,所以2a+5b=3,所以4a·32b=23=8.
考点一 幂的乘法运算
针对训练
整体思想
在应用幂的运算法则、乘法公式时,可以将一个代数式看做一个字母,这就是整体思想,应用这种思想方法解题,可以简化计算过程,且不易出错.
方法总结
要点梳理
整式的乘法
单项式与单项式相乘,把它们的________,
_____________分别相乘,对于只在一个单
项式中出现的字母,则连同它的指数一起作
为积的一个 .
单项式与多项式相乘,用 和_______
的每一项分别相乘,再把所得的积 .
多项式与多项式相乘,先用一个多项式的
_______与另一个多项式的 相乘,
再把所得的积 .
系数
相同字母的幂
因式
单项式
多项式
相加
每一项
每一项
相加
考点讲练
考点二 整式的乘法
例2 计算:[x(x2y2-xy)-y(x2-x3y)]×3x2y,其中 x=1,y=3.
解:原式=(x3y2-x2y-x2y+x3y2) ×3x2y
=(2x3y2-2x2y) ×3x2y
= 6x5y3-6x4y2 .
当x=1,y=3时,原式=6×27-6×9=108.
易错警示
在计算整式的加、减、乘、除、乘方的运算中, 一要注意运算顺序;二要熟练正确地运用运算法则.
考点讲练
针对训练
考点二 整式的乘法
1.一个长方形的长是a-2b+1,宽为a,则长方形的面积
为 .
a2-2ab+a
【解析】长方形的面积S=( a-2b+1 )· a=a2-2ab+a.
考点讲练
2.我们已知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一个代数恒等式也可以用这种形式来表示,例如(2a+b)(a+b)=2a2+3ab+b2,就可以用图①和图②等图形的面积表示.
a
a
a
b
b
ab
ab
ab
a2
a2
b2
b2
a2
a2
ab
ab
ab
a
a
a
b
b
图②
针对训练
(2)请画一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
图①
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
考点二 整式的乘法
考点讲练
(2)请画一个几何图形,使它的面积能表示
(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
图④
a2
b
a
ab
ab
ab
ab
b2
b2
b2
(2a+b)(a+2b)=2a2+5ab+2b2;
数形结合思想
考点二 整式的乘法
考点讲练
本章中数形结合思想主要体现在根据给定的图形写出一个代数恒等式或根据代数式画出几何图形. 由几何图形得到代数恒等式时,需要用不同的方法表示几何图形的面积,然后得出代数恒等式;由代数恒等式画图时,关键在于合理拼接,往往是相等的边拼到一起.
方法总结
考点二 整式的乘法
知识建构
下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2;
(2)(-3a-2)(3a-2)=9a2-4.
不对
改正:x2-4
不对
改正:
原式=(-2-3a)(-2+3a)
=(-2)2-(3a)2=4-9a2.
(3) (x -y)2 =x2 -y2
(4) (2x+y)2 =4x2 +2xy +y2
不对
改正:
x2-2xy +y2
不对
改正:
4x2+4xy +y2
要点梳理
乘法公式
公式名称 平方差公式 完全平方公式
文字表示 两数和与这两数的差的积,等于这两数的平方的差 两数和(差)的平方,等于这两数的_______加上(减去)_________的2倍
式子表示 (a+b)(a-b)= (a±b)2=
平方和
这两数积
a2-b2
a2±2ab+b2
要点梳理
乘法公式
公式的 常用变形 a2= (a-b)+b2; b2= -(a+b)(a-b). a2+b2=(a+b)2- , 或(a-b)2+ ;
(a+b)2=(a-b)2+ .
(a+b)
2ab
2ab
4ab
a2
方法点拨
(1)乘法公式实际上是一种特殊形式的多项式的乘法,公式的主要作用是简化运算;
(2)公式中的字母可以表示数,也可以表示其他单项式或多项式.
考点讲练
考点三 整式的乘法公式的运用
方法总结
例3 先化简,再求值:[(x-y)2+(x+y)(x-y)]-2x2,其中x=3,y=1.5.
【解析】运用完全平方公式和平方差公式,先算括号内的,再进行整式的减法运算.
解:原式=(x2-2xy+y2+x2-y2) -2x2
=(2x2-2xy) -2x2
=-2xy.
当x=3,y=1.5时,原式=-2×3×1.5 =-9.
整式的乘法公式包括平方差公式和完全平方公式,而完全平方公式又分为两个:两数和的完全平方公式和两数差的完全平方公式,在计算多项式的乘法时,对于符合这三个公式结构特征的式子,运用公式可减少运算量,提高解题速度.
考点讲练
针对训练
考点三 整式的乘法公式的运用
1.(2019春·罗湖区期末)下列关系式中,正确的是( )
A. (a-b)2 =a2-b2 B. (a+b) (a-b) =a2-b2
C. (a+b)2 =a2+b2 D. (a+b)2 =a2-2ab+b2
B
2.(2019春·福田区期末)先化简,再求值:
[ (2x-y)2 - (2x+y) (2x -y)]÷ y ,其中x=1, y =2.
解:原式=[4x2-4xy+y2- (4x2-y2)] ÷ y
= ( 4x2-4xy+y2-4x2+ y2) ÷ y
= (-4xy+2y2) ÷ y
= -4x+2y.
当x=1, y =2时,
原式=-4×1+2×2
=-4+4
=0.
回顾反思
转化思想
整体思想
数形结合思想
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
回顾与思考
北师大版初中数学七年级下册
第一章 整式的乘除
单项式
多项式
整式
你能举出几个整式的例子吗?
整式
①
②
③
④
⑤
⑥
①
②
③
④
⑤
⑥
整式的运算
你能根据上面的整式写出几个整式有关运算的式子吗?
①
②
( )
( )
( )
整式的加法
整式的减法
整式的加减
整式的乘除
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
整式的乘法
整式的除法
整式的乘法
(1)
(2)
(3)
(4)
(5)
(6)
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
整式的乘法
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
(1)
(5)
(3)
(4)
(2)
(6)
整式的乘法
单项式乘单项式:
单项式乘多项式:
多项式乘多项式:
(1)
(5)
(3)
(4)
(2)
(6)
整式的乘法
单项式乘单项式:
=
=
同底数幂的乘法
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
单项式与单项式相乘、相除
多项式与多项式相乘
幂的运算
同底数幂相乘
幂的乘方
同底数幂相除
整式的乘除法
乘法公式
知识建构
快速判断以下各题是否正确。
×
√
×
×
×
×
×
×
√
√
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
要点梳理
法则名称 文字表示 式子表示
同底数幂的乘法 同底数幂相乘, 底数 ,指数 . am an= (m、n为正整数)
幂的乘方 幂的乘方, 底数 ,指数 . (am)n= (m、n为正整数)
积的乘方 积的乘方,等于把积的每个因式分别 ,再把所得的幂 . (ab)n= (n为正整数)
am+n
amn
anbn
不变
相乘
相加
不变
相乘
乘方
[注意]
(1)其中的a、b可以 是单独的数、单独的字母,还可以是一个任意的代数式;
(2)这几个法则容易混淆,计算时必须先搞清楚该不该用法则、该用哪个法则.
要点梳理
同底数幂的除法
(1)同底数幂相除, 底数不变,指数相减.
(a≠0, m、n为任意整数)
(2)任何不等于零的数的零次幂都等于1.
(3)负整数指数幂:
(a≠0,n为正整数)
考点讲练
考点一 幂的乘法运算
例1 计算:
(1)(2a)3(b3)2 ·4a3b4; (2)(-8)2021 ×(0.125)2020.
解:(1)原式=8a3b6 ×4a3b4=32a3+3b6+4=2a6b10.
(2)原式=(-8)×(-8)2020 ×(0.125)2020
=(-8)[(-8) ×0.125]2020
=(-8)×(-1)2020=-8.
方法总结
幂的乘法运算包括同底数幂的乘法、幂的乘方、积的乘方.这三种运算性质贯穿全章,是整式乘法的基础.其逆向运用可将问题化繁为简,负数乘方结果的符号,奇次方得负,偶次方得正.
转化思想
转化思想将要解决的问题转化为另一个较易解决的问题,这是初中数学中常用的思想方法.如本章中,多项式×多项式 单项式×多项式 单项式×单项式 有理数的乘法和同底数幂的乘法.
考点讲练
考点一 幂的乘法运算
方法总结
考点讲练
考点一 幂的乘法运算
1.(2019·深圳)下列运算正确的是( )
A. a2 + a2 =a4 B. a3 · a4 =a12
C. (a3) 4=a12 D. (ab) 2=ab2
C
针对训练
解:∵420=(42)10=1610,
∴1610>1510,
∴420>1510.
2. 比较大小:420与1510.
转化思想
考点讲练
3. 若2a+5b-3=0,则4a·32b= .
【解析】已知条件是2a+5b-3=0,无法求出a,b的值. 因此可以逆用积的乘方先把4a·32b.化简为含有与已知条件相关的部分,即4a·32b=22a·25b=22a+5b.把2a+5b看做一个整体,因为2a+5b-3=0,所以2a+5b=3,所以4a·32b=23=8.
考点一 幂的乘法运算
针对训练
整体思想
在应用幂的运算法则、乘法公式时,可以将一个代数式看做一个字母,这就是整体思想,应用这种思想方法解题,可以简化计算过程,且不易出错.
方法总结
要点梳理
整式的乘法
单项式与单项式相乘,把它们的________,
_____________分别相乘,对于只在一个单
项式中出现的字母,则连同它的指数一起作
为积的一个 .
单项式与多项式相乘,用 和_______
的每一项分别相乘,再把所得的积 .
多项式与多项式相乘,先用一个多项式的
_______与另一个多项式的 相乘,
再把所得的积 .
系数
相同字母的幂
因式
单项式
多项式
相加
每一项
每一项
相加
考点讲练
考点二 整式的乘法
例2 计算:[x(x2y2-xy)-y(x2-x3y)]×3x2y,其中 x=1,y=3.
解:原式=(x3y2-x2y-x2y+x3y2) ×3x2y
=(2x3y2-2x2y) ×3x2y
= 6x5y3-6x4y2 .
当x=1,y=3时,原式=6×27-6×9=108.
易错警示
在计算整式的加、减、乘、除、乘方的运算中, 一要注意运算顺序;二要熟练正确地运用运算法则.
考点讲练
针对训练
考点二 整式的乘法
1.一个长方形的长是a-2b+1,宽为a,则长方形的面积
为 .
a2-2ab+a
【解析】长方形的面积S=( a-2b+1 )· a=a2-2ab+a.
考点讲练
2.我们已知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一个代数恒等式也可以用这种形式来表示,例如(2a+b)(a+b)=2a2+3ab+b2,就可以用图①和图②等图形的面积表示.
a
a
a
b
b
ab
ab
ab
a2
a2
b2
b2
a2
a2
ab
ab
ab
a
a
a
b
b
图②
针对训练
(2)请画一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
图①
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
考点二 整式的乘法
考点讲练
(2)请画一个几何图形,使它的面积能表示
(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
图④
a2
b
a
ab
ab
ab
ab
b2
b2
b2
(2a+b)(a+2b)=2a2+5ab+2b2;
数形结合思想
考点二 整式的乘法
考点讲练
本章中数形结合思想主要体现在根据给定的图形写出一个代数恒等式或根据代数式画出几何图形. 由几何图形得到代数恒等式时,需要用不同的方法表示几何图形的面积,然后得出代数恒等式;由代数恒等式画图时,关键在于合理拼接,往往是相等的边拼到一起.
方法总结
考点二 整式的乘法
知识建构
下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2;
(2)(-3a-2)(3a-2)=9a2-4.
不对
改正:x2-4
不对
改正:
原式=(-2-3a)(-2+3a)
=(-2)2-(3a)2=4-9a2.
(3) (x -y)2 =x2 -y2
(4) (2x+y)2 =4x2 +2xy +y2
不对
改正:
x2-2xy +y2
不对
改正:
4x2+4xy +y2
要点梳理
乘法公式
公式名称 平方差公式 完全平方公式
文字表示 两数和与这两数的差的积,等于这两数的平方的差 两数和(差)的平方,等于这两数的_______加上(减去)_________的2倍
式子表示 (a+b)(a-b)= (a±b)2=
平方和
这两数积
a2-b2
a2±2ab+b2
要点梳理
乘法公式
公式的 常用变形 a2= (a-b)+b2; b2= -(a+b)(a-b). a2+b2=(a+b)2- , 或(a-b)2+ ;
(a+b)2=(a-b)2+ .
(a+b)
2ab
2ab
4ab
a2
方法点拨
(1)乘法公式实际上是一种特殊形式的多项式的乘法,公式的主要作用是简化运算;
(2)公式中的字母可以表示数,也可以表示其他单项式或多项式.
考点讲练
考点三 整式的乘法公式的运用
方法总结
例3 先化简,再求值:[(x-y)2+(x+y)(x-y)]-2x2,其中x=3,y=1.5.
【解析】运用完全平方公式和平方差公式,先算括号内的,再进行整式的减法运算.
解:原式=(x2-2xy+y2+x2-y2) -2x2
=(2x2-2xy) -2x2
=-2xy.
当x=3,y=1.5时,原式=-2×3×1.5 =-9.
整式的乘法公式包括平方差公式和完全平方公式,而完全平方公式又分为两个:两数和的完全平方公式和两数差的完全平方公式,在计算多项式的乘法时,对于符合这三个公式结构特征的式子,运用公式可减少运算量,提高解题速度.
考点讲练
针对训练
考点三 整式的乘法公式的运用
1.(2019春·罗湖区期末)下列关系式中,正确的是( )
A. (a-b)2 =a2-b2 B. (a+b) (a-b) =a2-b2
C. (a+b)2 =a2+b2 D. (a+b)2 =a2-2ab+b2
B
2.(2019春·福田区期末)先化简,再求值:
[ (2x-y)2 - (2x+y) (2x -y)]÷ y ,其中x=1, y =2.
解:原式=[4x2-4xy+y2- (4x2-y2)] ÷ y
= ( 4x2-4xy+y2-4x2+ y2) ÷ y
= (-4xy+2y2) ÷ y
= -4x+2y.
当x=1, y =2时,
原式=-4×1+2×2
=-4+4
=0.
回顾反思
转化思想
整体思想
数形结合思想
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
