初中数学北师大版七年级下册第四章 三角形第四章《三角形》回顾与思考 (共16张ppt)
文档属性
| 名称 | 初中数学北师大版七年级下册第四章 三角形第四章《三角形》回顾与思考 (共16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 07:44:13 | ||
图片预览




文档简介
(共16张PPT)
回顾与思考
第四章 三角形
图形的全等
三角形的概念及表示
三角形三边的关系、三内角的关系
图形全等的概念和性质
全等三角形
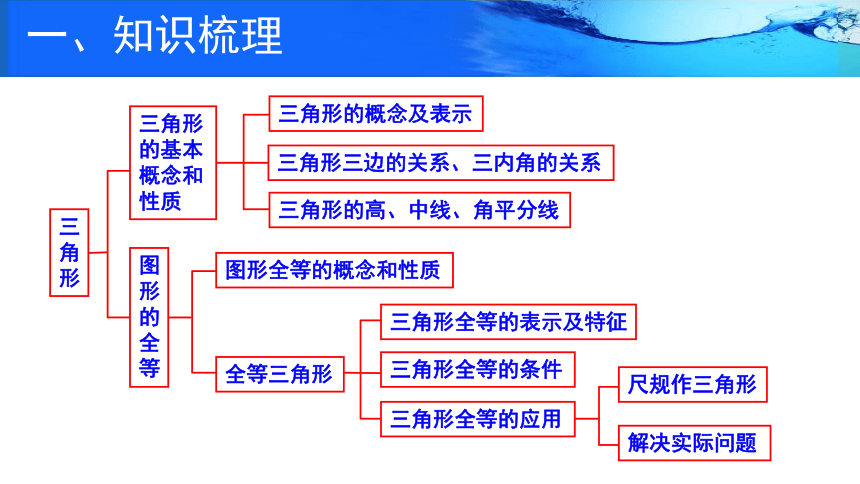
一、知识梳理
三角形全等的表示及特征
三角形全等的应用
三角形全等的条件
尺规作三角形
解决实际问题
三角形
三角形的基本概念和性质
三角形的高、中线、角平分线
1.三角形:
三角形的任意两边之和大于第三边,任意两边之差小于第三边.
一、知识梳理
三条线段
三角形
不在同一直线上
首尾顺次相接
2.三角形的三角关系:
(1)三角形的内角和等于180度;
(2)直角三角形的两个锐角互余.
如图,△ABC中,∠A+∠B+∠C=180°;
Rt△ABC中,∠C=90°,则∠A+∠B=90°.
3.三角形的三边关系:
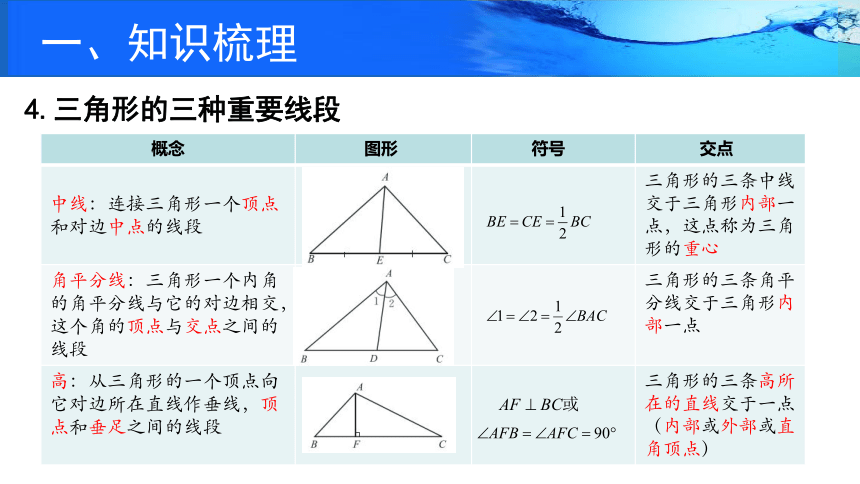
4.三角形的三种重要线段
一、知识梳理
概念 图形 符号 交点
中线:连接三角形一个顶点和对边中点的线段 三角形的三条中线交于三角形内部一点,这点称为三角形的重心
角平分线:三角形一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段 三角形的三条角平分线交于三角形内部一点
高:从三角形的一个顶点向它对边所在直线作垂线,顶点和垂足之间的线段 三角形的三条高所在的直线交于一点(内部或外部或直角顶点)
4.图形的全等
一、知识梳理
(1)
(2)全等图形的 和 都相同.
(3)全等三角形的 相等, 相等.
(4)全等三角形的判定方法有 、 、 、 .
边边边
形状
大小
对应边
对应角
能够完全重合
角边角
边角边
角角边
两个图形
全等图形
△ABC≌△DEF
注意:两边和其中一边的对角对应相等的两个三角形不一定全等.
二、基础演练
1.在△ABC中,∠C=70°,∠A=50°,则∠B= 度,这个三角形按角
分类是 三角形.
60
2.已知一个等腰三角形的一边长2cm,另一边长9cm ,则这个三角形
的周长是 .
20cm
锐角
3.三角形的下列线段中能将三角形的面积分成相等两部分的是( ).
A. 中线 B. 角平分线 C. 高 D. 以上都不对
A
4.如右图所示,AD是△ABC的角平分线,
且∠BAD=35°,∠C=60°,则∠B为
度.
50
①2,2,9
②9,9,2
√
×
D
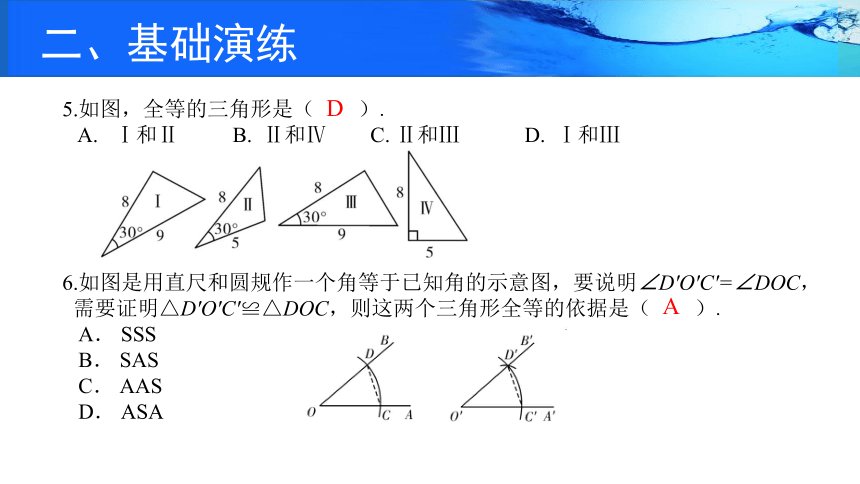
5.如图,全等的三角形是( ).
A. Ⅰ和Ⅱ B. Ⅱ和Ⅳ C. Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
6.如图是用直尺和圆规作一个角等于已知角的示意图,要说明∠D′O′C′=∠DOC,
需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( ).
A. SSS
B. SAS
C. AAS
D. ASA
A
二、基础演练
三、典例解析
例1.如图,在△ABC中,∠B=30°,∠C=50°,AD和AE分别是△ABC的
高和角平分线,求∠DAE的度数.
解:
(三角形的内角和是180°)
(直角三角形的两个锐角互余)
三、典例解析
例2.(1)如图1,AB=DF,AC=DE,BE=CF.BC与FE相等吗?你能找到一
对全等三角形吗?说明你的理由.
解:
BC=FE,△ABC≌△DFE.理由如下:
∵BE=CF
∴BE+CE=CF+CE
即BC=FE
在△ABC和△DFE中
AB=DF
AC=DE
BC=FE
∴△ABC≌△DFE
(SSS)
(等式的性质)
图1
三、典例解析
例2.(1)如图1,AB=DF,AC=DE,BE=CF.BC与FE相等吗?你能找到一
对全等三角形吗?说明你的理由.
(2)若△DEF翻折到如图2所示的位置,已知条件不变,则(1)中的结
论仍然成立吗?你还能发现什么结论?
分析:同(1)可知
BC=FE,△ABC≌△DFE
∠A=∠D
∠B=∠F
∠ACB=∠DEF
AB∥DF
AC∥DE
∠ACF=∠DEB
图1
图2
三、典例解析
例3.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件
是 (只需添加一个你认为合适的条件).
分析:现在我们已知 角→∠ABC=∠DCB
边→BC=CB(公共边)
SAS
ASA
AAS
①用 ,需要补充条件AB=DC
②用 ,需要补充条件∠ACB=∠DBC
③用 ,需要补充条件∠A=∠D
AB=DC
∠ACB=∠DBC
∠A=∠D
四、归纳提炼
判定三角形全等的基本思路
1.已知两边
对应相等
找夹角对应相等
找第三边对应相等
2.已知两角
对应相等
找任意一边对应相等
(SAS)
(SSS)
(ASA或AAS)
(AAS)
3.已知一边
一角对应相等
边是角的对边
边是角的邻边
找另一角对应相等
(SAS)
找夹该角的另一边对应相等
找另一角对应相等
(ASA或AAS)
几种常见的全等三角形基本图形
四、归纳提炼
在△ABC中,∠BAC=90°,AB=AC,直线EF经过点A,且BE⊥EF于点E,CF⊥EF于点F.
(1)当直线EF绕点A旋转到图1的位置时,
求证:①△ABE≌△CAF;②EF=BE+CF.
解:①
∵BE⊥EF,CF⊥EF
∴∠AEB=∠CFA=90°
∴∠1+∠2=90°
∵∠BAC=90°
∴∠1+∠3=90°
∴∠2=∠3
在△ABE和△CAF中
∠2=∠3
∠AEB=∠CFA
AB=AC
∴△ABE≌△CAF
(AAS)
②∵△ABE≌△CAF
∴BE=AF,AE=CF
∵EF=AF+AE
∴EF=BE+CF
(全等三角形的对应边相等)
1
2
3
1
2
3
(同角的余角相等)
五、拓展提升
图1
在△ABC中,∠BAC=90°,AB=AC,直线EF经过点A,且BE⊥EF于点E,CF⊥EF于点F.
(1)当直线EF绕点A旋转到图1的位置时,
求证:①△ABE≌△CAF;②EF=BE+CF.
(2)当直线EF绕点A旋转到图2的位置时,你能得到BE、CF与EF的数
量关系吗?说明你的理由.
1
2
3
分析:同(1)可知
BE=AF,AE=CF
△ABE≌△CAF
2
1
3
五、拓展提升
图1
图2
EF=BE-CF
EF=AF-AE
再 见
回顾与思考
第四章 三角形
图形的全等
三角形的概念及表示
三角形三边的关系、三内角的关系
图形全等的概念和性质
全等三角形
一、知识梳理
三角形全等的表示及特征
三角形全等的应用
三角形全等的条件
尺规作三角形
解决实际问题
三角形
三角形的基本概念和性质
三角形的高、中线、角平分线
1.三角形:
三角形的任意两边之和大于第三边,任意两边之差小于第三边.
一、知识梳理
三条线段
三角形
不在同一直线上
首尾顺次相接
2.三角形的三角关系:
(1)三角形的内角和等于180度;
(2)直角三角形的两个锐角互余.
如图,△ABC中,∠A+∠B+∠C=180°;
Rt△ABC中,∠C=90°,则∠A+∠B=90°.
3.三角形的三边关系:
4.三角形的三种重要线段
一、知识梳理
概念 图形 符号 交点
中线:连接三角形一个顶点和对边中点的线段 三角形的三条中线交于三角形内部一点,这点称为三角形的重心
角平分线:三角形一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段 三角形的三条角平分线交于三角形内部一点
高:从三角形的一个顶点向它对边所在直线作垂线,顶点和垂足之间的线段 三角形的三条高所在的直线交于一点(内部或外部或直角顶点)
4.图形的全等
一、知识梳理
(1)
(2)全等图形的 和 都相同.
(3)全等三角形的 相等, 相等.
(4)全等三角形的判定方法有 、 、 、 .
边边边
形状
大小
对应边
对应角
能够完全重合
角边角
边角边
角角边
两个图形
全等图形
△ABC≌△DEF
注意:两边和其中一边的对角对应相等的两个三角形不一定全等.
二、基础演练
1.在△ABC中,∠C=70°,∠A=50°,则∠B= 度,这个三角形按角
分类是 三角形.
60
2.已知一个等腰三角形的一边长2cm,另一边长9cm ,则这个三角形
的周长是 .
20cm
锐角
3.三角形的下列线段中能将三角形的面积分成相等两部分的是( ).
A. 中线 B. 角平分线 C. 高 D. 以上都不对
A
4.如右图所示,AD是△ABC的角平分线,
且∠BAD=35°,∠C=60°,则∠B为
度.
50
①2,2,9
②9,9,2
√
×
D
5.如图,全等的三角形是( ).
A. Ⅰ和Ⅱ B. Ⅱ和Ⅳ C. Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
6.如图是用直尺和圆规作一个角等于已知角的示意图,要说明∠D′O′C′=∠DOC,
需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( ).
A. SSS
B. SAS
C. AAS
D. ASA
A
二、基础演练
三、典例解析
例1.如图,在△ABC中,∠B=30°,∠C=50°,AD和AE分别是△ABC的
高和角平分线,求∠DAE的度数.
解:
(三角形的内角和是180°)
(直角三角形的两个锐角互余)
三、典例解析
例2.(1)如图1,AB=DF,AC=DE,BE=CF.BC与FE相等吗?你能找到一
对全等三角形吗?说明你的理由.
解:
BC=FE,△ABC≌△DFE.理由如下:
∵BE=CF
∴BE+CE=CF+CE
即BC=FE
在△ABC和△DFE中
AB=DF
AC=DE
BC=FE
∴△ABC≌△DFE
(SSS)
(等式的性质)
图1
三、典例解析
例2.(1)如图1,AB=DF,AC=DE,BE=CF.BC与FE相等吗?你能找到一
对全等三角形吗?说明你的理由.
(2)若△DEF翻折到如图2所示的位置,已知条件不变,则(1)中的结
论仍然成立吗?你还能发现什么结论?
分析:同(1)可知
BC=FE,△ABC≌△DFE
∠A=∠D
∠B=∠F
∠ACB=∠DEF
AB∥DF
AC∥DE
∠ACF=∠DEB
图1
图2
三、典例解析
例3.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件
是 (只需添加一个你认为合适的条件).
分析:现在我们已知 角→∠ABC=∠DCB
边→BC=CB(公共边)
SAS
ASA
AAS
①用 ,需要补充条件AB=DC
②用 ,需要补充条件∠ACB=∠DBC
③用 ,需要补充条件∠A=∠D
AB=DC
∠ACB=∠DBC
∠A=∠D
四、归纳提炼
判定三角形全等的基本思路
1.已知两边
对应相等
找夹角对应相等
找第三边对应相等
2.已知两角
对应相等
找任意一边对应相等
(SAS)
(SSS)
(ASA或AAS)
(AAS)
3.已知一边
一角对应相等
边是角的对边
边是角的邻边
找另一角对应相等
(SAS)
找夹该角的另一边对应相等
找另一角对应相等
(ASA或AAS)
几种常见的全等三角形基本图形
四、归纳提炼
在△ABC中,∠BAC=90°,AB=AC,直线EF经过点A,且BE⊥EF于点E,CF⊥EF于点F.
(1)当直线EF绕点A旋转到图1的位置时,
求证:①△ABE≌△CAF;②EF=BE+CF.
解:①
∵BE⊥EF,CF⊥EF
∴∠AEB=∠CFA=90°
∴∠1+∠2=90°
∵∠BAC=90°
∴∠1+∠3=90°
∴∠2=∠3
在△ABE和△CAF中
∠2=∠3
∠AEB=∠CFA
AB=AC
∴△ABE≌△CAF
(AAS)
②∵△ABE≌△CAF
∴BE=AF,AE=CF
∵EF=AF+AE
∴EF=BE+CF
(全等三角形的对应边相等)
1
2
3
1
2
3
(同角的余角相等)
五、拓展提升
图1
在△ABC中,∠BAC=90°,AB=AC,直线EF经过点A,且BE⊥EF于点E,CF⊥EF于点F.
(1)当直线EF绕点A旋转到图1的位置时,
求证:①△ABE≌△CAF;②EF=BE+CF.
(2)当直线EF绕点A旋转到图2的位置时,你能得到BE、CF与EF的数
量关系吗?说明你的理由.
1
2
3
分析:同(1)可知
BE=AF,AE=CF
△ABE≌△CAF
2
1
3
五、拓展提升
图1
图2
EF=BE-CF
EF=AF-AE
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
