内蒙古自治区巴彦淖尔市临河三高2022届高三上学期12月第二次阶段性测试数学(理)试题(Word版含答案)
文档属性
| 名称 | 内蒙古自治区巴彦淖尔市临河三高2022届高三上学期12月第二次阶段性测试数学(理)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 772.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 11:12:06 | ||
图片预览



文档简介
临河三高2021—2022学年上学期高三年级第二次阶段性测试
(理科数学)试卷
试卷总分:150分 考试时间:120分钟
姓名:___________ 班级:___________ 考号:___________
注意事项:
1.答卷前,务必将自己的姓名、准考证号等填写在试卷和答题卡上,并正确粘贴条形码。
2.选择题答案用2B铅笔把答题卡对应题目的答案标号涂黑。非选择题用0.5毫米黑色字迹笔将答案写在答题卡指定位置。在试卷上答题无效。
3.考试结束后,只交答题卡,试卷自己保留,以备讲评使用。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,则( )
A. B. C. D.
2.已知向量和不共线,向量,若三点共线,则( )
A.3 B.2 C.1 D.
3.设等差数列的前项和为,若,则公差=( )
A.-3 B.2 C.3 D.6
4.公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟领先他10米,当阿基里斯跑完下一个10米时,乌龟领先他1米.所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为0.001米时,乌龟爬行的总距离为( )
A.米 B.米 C.米 D.米
5.下列结论正确的是
A. 若,则是锐角三角形
B. “”是“函数在区间上为增函数”的充要条件
C.
D. 若三点满足,则三点共线
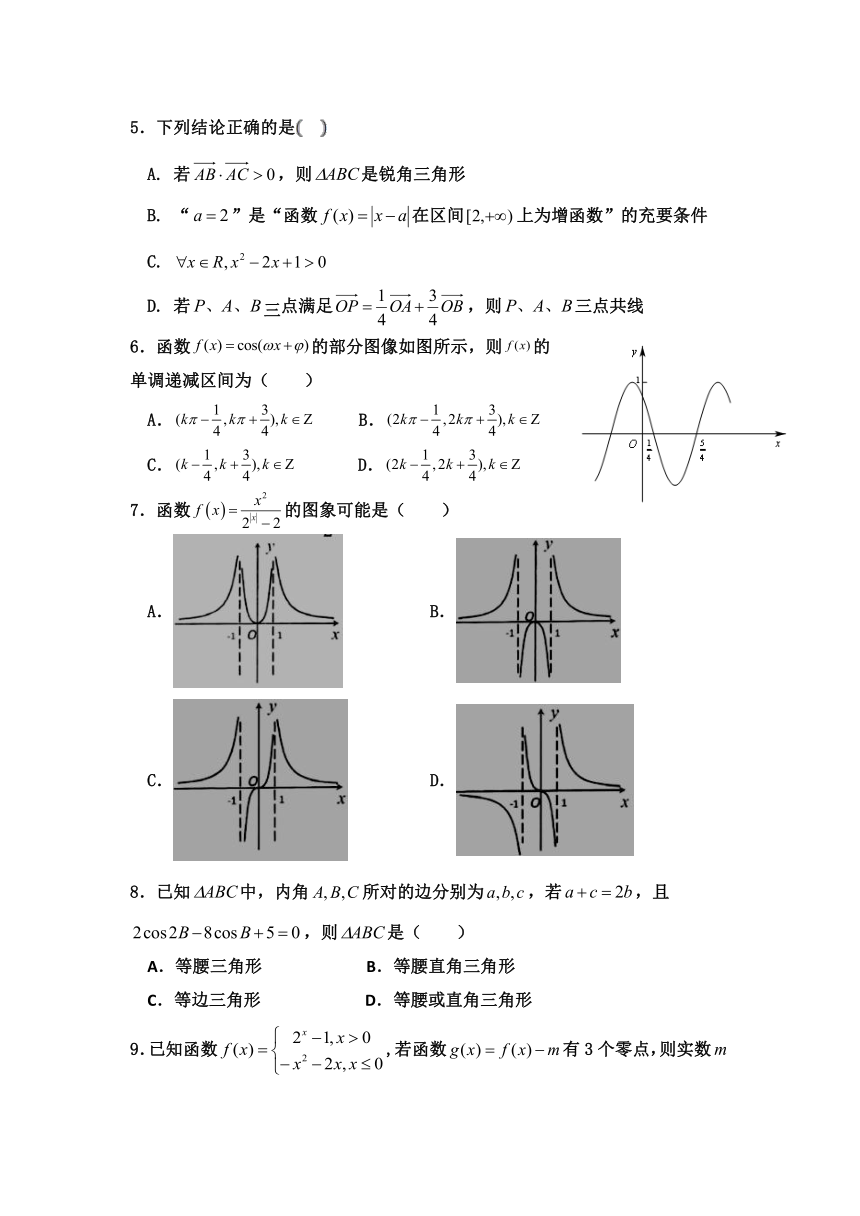
6.函数的部分图像如图所示,则的
单调递减区间为( )
A. B.
C. D.
7.函数的图象可能是( )
A. B.
C. D.
8.已知中,内角所对的边分别为,若,且,则是( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.等腰或直角三角形
9.已知函数,若函数有3个零点,则实数的取值范围是( )
A. B. C. D.
10.已知函数对任意的都满足为偶函数,
当时,,则
A. B. C. D.
11.已知数列满足,则数列的前10项和( )
A. B. C. D.
12.设,其中是自然对数的底数,则( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分)
13.已知向量.若,则________.
14.在各项均为正数的等比数列中,且,,成等差数列,记是数列的前项和,则________.
15.设.则的值为______
16.声音是物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数
,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是________.(填序号)
①是的一个周期;②在上有3个零点;
③的最大值为;④在上是增函数.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题10分)
有一正项等比数列的公比为,前项和为,满足.
设.
(1)求出数列的通项公式;
(2)记,求数列的前项和.
18.(本题12分)
函数,.
(1)求的最小正周期及其单调递增区间;
(2)把图象上所有的点的横坐标变为原来的2倍,再把函数图象上所有的点向左平移个
单位长度,得到函数的图象,在区间上的最大值和最小值.
19.(本题12分)
中,内角所对的边分别为,.
(1)求;
(2)如图,为边上一点,,求的面积.
20.(本题12分)
已知函数.
(1)求曲线在点处的切线方程;
(2)求函数在区间上的最大值;
21.(本题12分)
已知数列的前项和为,且.
(1)求的通项公式;
(2)已知,求数列的前项和,并证明.
22.(本题12分)
已知函数.
(1)若函数与有相同的极值点,求实数的值;
(2)若,讨论的单调性.
临河三高2021—2022学年上学期高三年级第二次阶段性测试
(理科数学)答案
1、选择题 DACAD DBCCA BA
1、填空题 126 ①②③
17.(1)an=2×2n-1=2n(n∈N*);(2).
【详解】(1)由a2a4=64,得=64.又∵an>0,∴a3=8.∵S3=a1+a2+a3,∴a1+a2+8=14,∴a1+a1q=6,即a1(1+q)=6,∴(1+q)=6,即3q2-4q-4=0,解得q=2或q=-(舍去).∴a1=2,a2=4,an=2×2n-1=2n(n∈N*).
(2)∴Tn=c1+c2+c3+…+cn=
18. (1)最小正周期为,单调递增区间为;
(2)的最小值为,最大值为
【详解】(1)函数
.
即的解析式为,所以函数的最小正周期为,
令
所以,的单调递增区间为
(2)把图像上的点的横坐标变为原来的2倍,得到函数,
再把图像上所有的点向左平移个单位长度,可得,
所以,的最小值为,最大值为
19.(1);(2).
【详解】(1),
由正弦定理,可得,,,,,则,.
(2),,,又,
在中,由余弦定理,可得:,
即,解得,,又,.
20.(1);(2).
【详解】已知定义域为,,
所以曲线在点处的切线方程为即.
(2),,
令,则,或,在上单调递增;令,则,,在上单调递减;,函数在单调递减,在单调递增.
时,时,.又,函数在上的最大值是1;
21.(1),(2);证明见解析
【详解】(1)当时,由,得或(舍去),由①,
当时,,②,由①-②,得,
整理得,因为,所以.
所以是首项为1,公差为1的等差数列,故数列的通项公式为.
(2),,①,
②,
由①-②可得,
,,,.
22.(1)1;(2)证明见解析.
【详解】(1)的定义域为,,由得,易知函数在单调递增,在单调递减,故函数的极大值点为,,依题意有,解得,经验证符合题意,故.
由题知,
当时,恒成立,所以在上单调递增;
当时,令,所以在上单调递减,
令,所以在上单调递增;
综上所述,当时,在上单调递增,
当时,在上单调递减,在上单调递增.
(理科数学)试卷
试卷总分:150分 考试时间:120分钟
姓名:___________ 班级:___________ 考号:___________
注意事项:
1.答卷前,务必将自己的姓名、准考证号等填写在试卷和答题卡上,并正确粘贴条形码。
2.选择题答案用2B铅笔把答题卡对应题目的答案标号涂黑。非选择题用0.5毫米黑色字迹笔将答案写在答题卡指定位置。在试卷上答题无效。
3.考试结束后,只交答题卡,试卷自己保留,以备讲评使用。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,则( )
A. B. C. D.
2.已知向量和不共线,向量,若三点共线,则( )
A.3 B.2 C.1 D.
3.设等差数列的前项和为,若,则公差=( )
A.-3 B.2 C.3 D.6
4.公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟领先他10米,当阿基里斯跑完下一个10米时,乌龟领先他1米.所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为0.001米时,乌龟爬行的总距离为( )
A.米 B.米 C.米 D.米
5.下列结论正确的是
A. 若,则是锐角三角形
B. “”是“函数在区间上为增函数”的充要条件
C.
D. 若三点满足,则三点共线
6.函数的部分图像如图所示,则的
单调递减区间为( )
A. B.
C. D.
7.函数的图象可能是( )
A. B.
C. D.
8.已知中,内角所对的边分别为,若,且,则是( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.等腰或直角三角形
9.已知函数,若函数有3个零点,则实数的取值范围是( )
A. B. C. D.
10.已知函数对任意的都满足为偶函数,
当时,,则
A. B. C. D.
11.已知数列满足,则数列的前10项和( )
A. B. C. D.
12.设,其中是自然对数的底数,则( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分)
13.已知向量.若,则________.
14.在各项均为正数的等比数列中,且,,成等差数列,记是数列的前项和,则________.
15.设.则的值为______
16.声音是物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数
,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是________.(填序号)
①是的一个周期;②在上有3个零点;
③的最大值为;④在上是增函数.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本题10分)
有一正项等比数列的公比为,前项和为,满足.
设.
(1)求出数列的通项公式;
(2)记,求数列的前项和.
18.(本题12分)
函数,.
(1)求的最小正周期及其单调递增区间;
(2)把图象上所有的点的横坐标变为原来的2倍,再把函数图象上所有的点向左平移个
单位长度,得到函数的图象,在区间上的最大值和最小值.
19.(本题12分)
中,内角所对的边分别为,.
(1)求;
(2)如图,为边上一点,,求的面积.
20.(本题12分)
已知函数.
(1)求曲线在点处的切线方程;
(2)求函数在区间上的最大值;
21.(本题12分)
已知数列的前项和为,且.
(1)求的通项公式;
(2)已知,求数列的前项和,并证明.
22.(本题12分)
已知函数.
(1)若函数与有相同的极值点,求实数的值;
(2)若,讨论的单调性.
临河三高2021—2022学年上学期高三年级第二次阶段性测试
(理科数学)答案
1、选择题 DACAD DBCCA BA
1、填空题 126 ①②③
17.(1)an=2×2n-1=2n(n∈N*);(2).
【详解】(1)由a2a4=64,得=64.又∵an>0,∴a3=8.∵S3=a1+a2+a3,∴a1+a2+8=14,∴a1+a1q=6,即a1(1+q)=6,∴(1+q)=6,即3q2-4q-4=0,解得q=2或q=-(舍去).∴a1=2,a2=4,an=2×2n-1=2n(n∈N*).
(2)∴Tn=c1+c2+c3+…+cn=
18. (1)最小正周期为,单调递增区间为;
(2)的最小值为,最大值为
【详解】(1)函数
.
即的解析式为,所以函数的最小正周期为,
令
所以,的单调递增区间为
(2)把图像上的点的横坐标变为原来的2倍,得到函数,
再把图像上所有的点向左平移个单位长度,可得,
所以,的最小值为,最大值为
19.(1);(2).
【详解】(1),
由正弦定理,可得,,,,,则,.
(2),,,又,
在中,由余弦定理,可得:,
即,解得,,又,.
20.(1);(2).
【详解】已知定义域为,,
所以曲线在点处的切线方程为即.
(2),,
令,则,或,在上单调递增;令,则,,在上单调递减;,函数在单调递减,在单调递增.
时,时,.又,函数在上的最大值是1;
21.(1),(2);证明见解析
【详解】(1)当时,由,得或(舍去),由①,
当时,,②,由①-②,得,
整理得,因为,所以.
所以是首项为1,公差为1的等差数列,故数列的通项公式为.
(2),,①,
②,
由①-②可得,
,,,.
22.(1)1;(2)证明见解析.
【详解】(1)的定义域为,,由得,易知函数在单调递增,在单调递减,故函数的极大值点为,,依题意有,解得,经验证符合题意,故.
由题知,
当时,恒成立,所以在上单调递增;
当时,令,所以在上单调递减,
令,所以在上单调递增;
综上所述,当时,在上单调递增,
当时,在上单调递减,在上单调递增.
同课章节目录
