新人教版九年级上册24.1.4圆周角(第一课时)
文档属性
| 名称 | 新人教版九年级上册24.1.4圆周角(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 168.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 21:34:31 | ||
图片预览





文档简介
课件29张PPT。24.1.4 圆周角
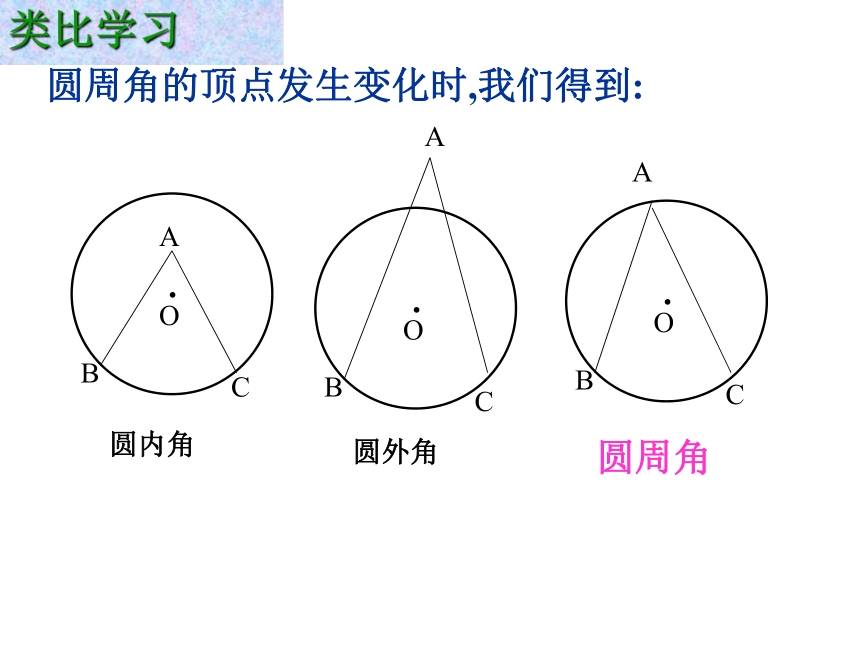
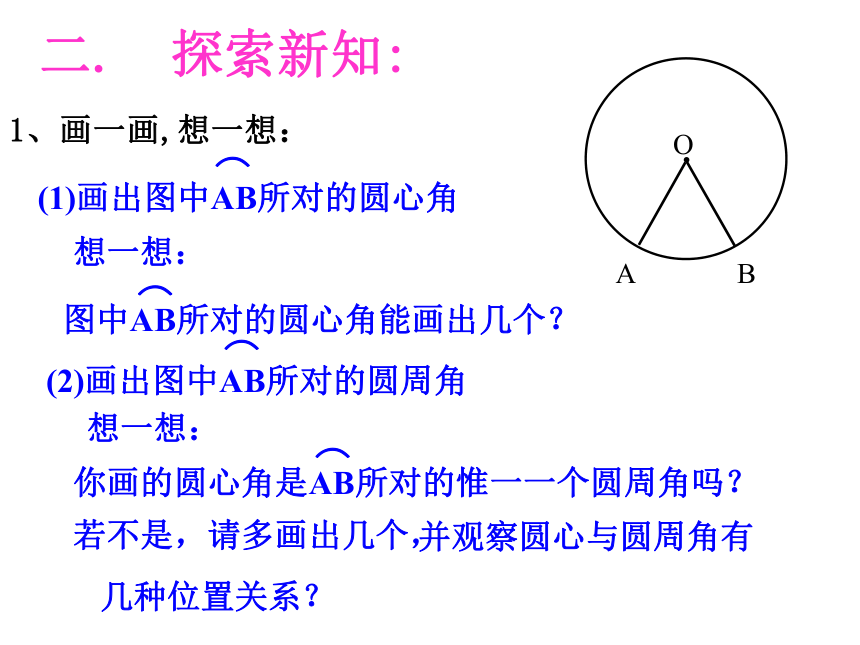
第一课时一. 复习引入:1.圆心角是怎样定义的?顶点在圆心的角叫圆心角2. 你能仿照圆心角的定义,给上图中像∠ACB这样的角下个定义吗?C圆周角:顶点在圆上,角的两边与圆相交。判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是练习:圆周角的顶点发生变化时,我们得到:A.OBCAA圆内角圆外角圆周角类比学习二. 探索新知:OAB1、画一画,想一想:想一想:想一想:若不是,请多画出几个, 并观察圆心与圆周角有
几种位置关系?二. 探索新知:2、猜一猜:观察你所画的圆周角之间有什么数量关系?圆心角与圆周角呢?你能用文字语言表达你的发现吗? 同弧所对的圆周角相等,
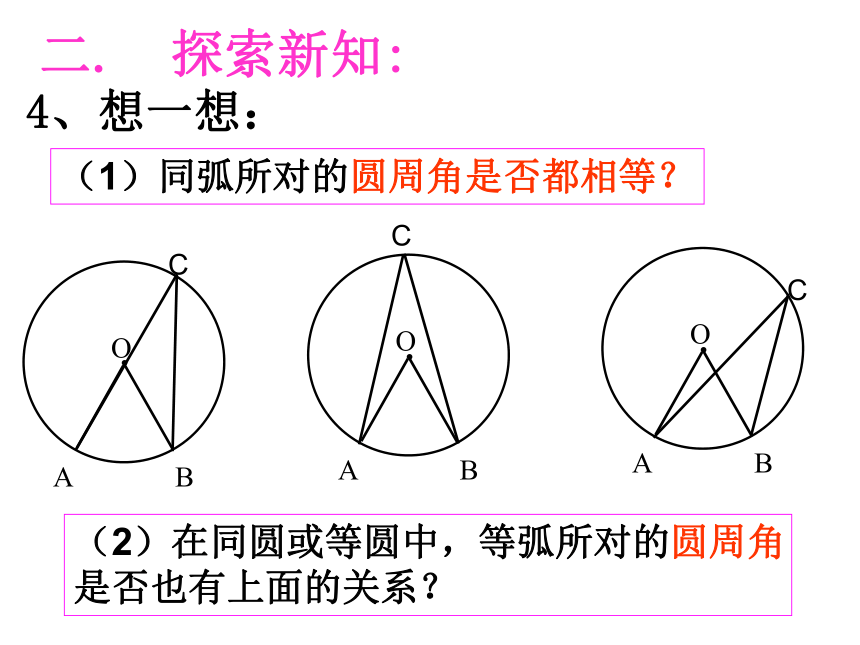
都等于它所对的圆心角的一半.二. 探索新知:3、证一证:CCC同弧所对的圆周角等于它所对的圆心角的一半.二. 探索新知:4、想一想:CCC(1)同弧所对的圆周角是否都相等?(2)在同圆或等圆中,等弧所对的圆周角
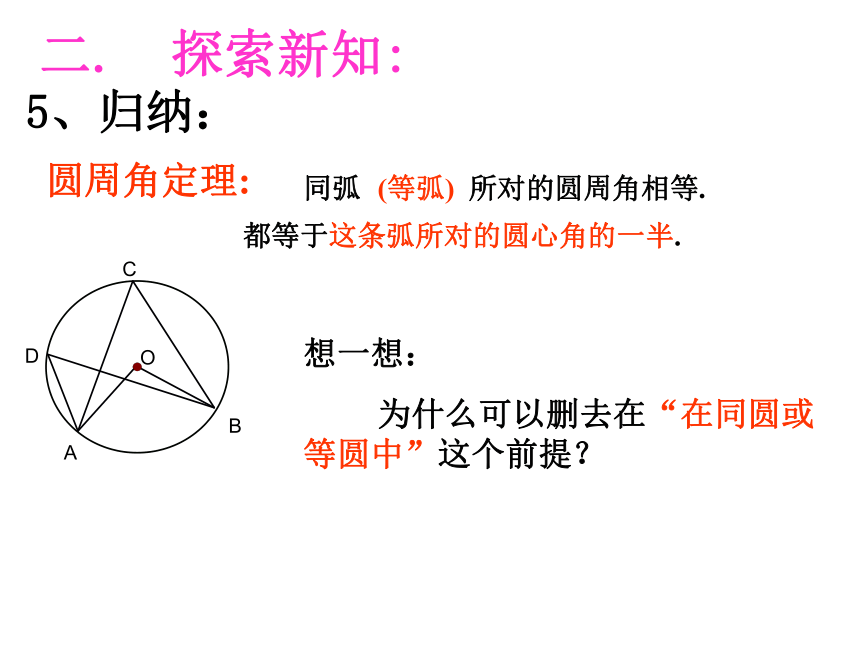
是否也有上面的关系?同弧 所对的圆周角相等.(等弧)都等于这条弧所对的圆心角的一半.圆周角定理:二. 探索新知:5、归纳:想一想:
为什么可以删去在“在同圆或等圆中”这个前提?二. 探索新知:6、试一试
(1)求下图中各个x的值。C(2).试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8二. 探索新知:6、试一试二. 探索新知:7、想一想如图,AB是直径,则圆心角∠AOB=___,圆周角∠AC1B=___, ∠AC2B=___, ∠AC3B=___。180°90°90°90°从上面的问题中你能得到什么结论?它的逆命题成立吗?半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。圆周角定理的推论:求图中x的度数二. 探索新知:8、试一试40°x三.应用新知:例、如图,圆O的直径AB=10cm,弦AC=6cm,
∠ ACB的平分线交圆O于点D。
求BC、AD、BD的长。130°三.应用新知:练习2、如图,AB是圆O的直径,CD⊥AB,垂足为E,若 ∠ACD=30 °,AE=2cm.求DB的长。3.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。∠BOC =140° 三.应用新知:练习 这节课你在知识学习和探究方法方面有什么收获?四.课堂小结:还有哪些疑惑?四.今天作业:课时作业本 P80---81例2: 如图,AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.1062:已知⊙O中弦AB的等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。3.如图,∠A是圆O的圆周角, ∠A=40°,求∠OBC的度数。 练习:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°130°40°x三.应用新知:猜想:?思考1:圆心与圆周角的位置有哪些关系?同弧所对的圆周角等于它所对的圆心角的一半.圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系圆周角和圆心角的关系3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC= ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.
第一课时一. 复习引入:1.圆心角是怎样定义的?顶点在圆心的角叫圆心角2. 你能仿照圆心角的定义,给上图中像∠ACB这样的角下个定义吗?C圆周角:顶点在圆上,角的两边与圆相交。判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是练习:圆周角的顶点发生变化时,我们得到:A.OBCAA圆内角圆外角圆周角类比学习二. 探索新知:OAB1、画一画,想一想:想一想:想一想:若不是,请多画出几个, 并观察圆心与圆周角有
几种位置关系?二. 探索新知:2、猜一猜:观察你所画的圆周角之间有什么数量关系?圆心角与圆周角呢?你能用文字语言表达你的发现吗? 同弧所对的圆周角相等,
都等于它所对的圆心角的一半.二. 探索新知:3、证一证:CCC同弧所对的圆周角等于它所对的圆心角的一半.二. 探索新知:4、想一想:CCC(1)同弧所对的圆周角是否都相等?(2)在同圆或等圆中,等弧所对的圆周角
是否也有上面的关系?同弧 所对的圆周角相等.(等弧)都等于这条弧所对的圆心角的一半.圆周角定理:二. 探索新知:5、归纳:想一想:
为什么可以删去在“在同圆或等圆中”这个前提?二. 探索新知:6、试一试
(1)求下图中各个x的值。C(2).试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8二. 探索新知:6、试一试二. 探索新知:7、想一想如图,AB是直径,则圆心角∠AOB=___,圆周角∠AC1B=___, ∠AC2B=___, ∠AC3B=___。180°90°90°90°从上面的问题中你能得到什么结论?它的逆命题成立吗?半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。圆周角定理的推论:求图中x的度数二. 探索新知:8、试一试40°x三.应用新知:例、如图,圆O的直径AB=10cm,弦AC=6cm,
∠ ACB的平分线交圆O于点D。
求BC、AD、BD的长。130°三.应用新知:练习2、如图,AB是圆O的直径,CD⊥AB,垂足为E,若 ∠ACD=30 °,AE=2cm.求DB的长。3.AB、AC为⊙O的两条弦,延长CA到D,使 AD=AB,如果∠ADB=35° ,
求∠BOC的度数。∠BOC =140° 三.应用新知:练习 这节课你在知识学习和探究方法方面有什么收获?四.课堂小结:还有哪些疑惑?四.今天作业:课时作业本 P80---81例2: 如图,AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.1062:已知⊙O中弦AB的等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。3.如图,∠A是圆O的圆周角, ∠A=40°,求∠OBC的度数。 练习:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°130°40°x三.应用新知:猜想:?思考1:圆心与圆周角的位置有哪些关系?同弧所对的圆周角等于它所对的圆心角的一半.圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系圆周角和圆心角的关系3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC= ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.
同课章节目录
