新人教版九年级上册24.2.1点与圆的位置关系(第二课时)
文档属性
| 名称 | 新人教版九年级上册24.2.1点与圆的位置关系(第二课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览






文档简介
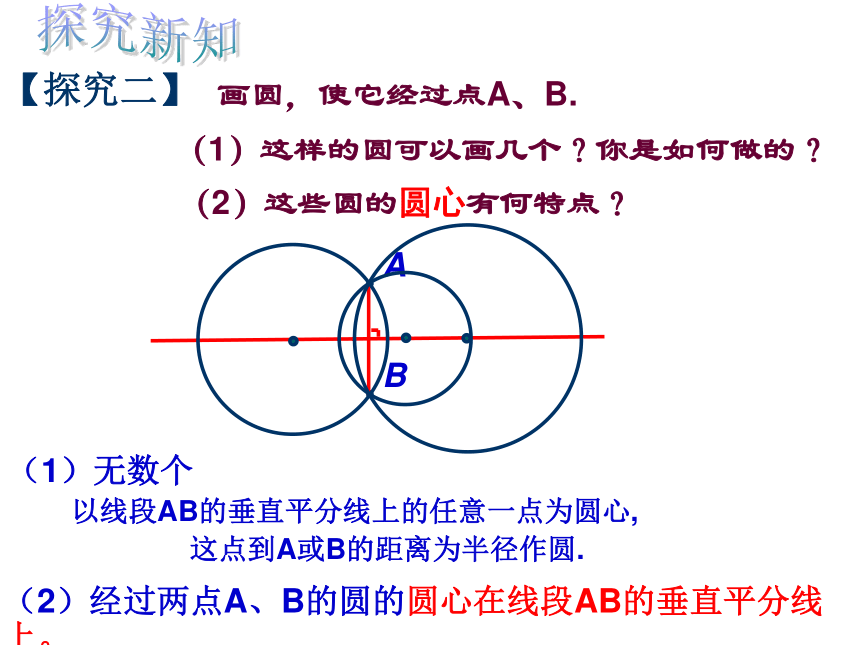
课件28张PPT。复习回顾点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r设⊙O的半径为r,点到圆心的距离为d,判断方法2在平面直角坐标系中,O为坐标原点,⊙O经过点P(1,1),判断下列各点与⊙O的的位置关系:(1)A(-1,1)(2) B (1,0)(3)C(2,2)作业分析24.2.1 点与圆的位置关系第二课时如图是一个破残的圆形轮片,李师傅想要浇铸一个同样大小的圆轮,你能想办法帮李师傅的忙吗?情景引入画圆,使它经过已知点A.解:(1)无数个(2)平面上除A点外的任意一点探究新知【探究一】(1)这样的圆你能画出几个?(2)这些圆的圆心的位置分布是否有规律?画圆,使它经过点A、B.(2)经过两点A、B的圆的圆心在线段AB的垂直平分线上。
(2)这些圆的圆心有何特点?探究新知【探究二】(1)这样的圆可以画几个?你是如何做的?(1)无数个
以线段AB的垂直平分线上的任意一点为圆心,
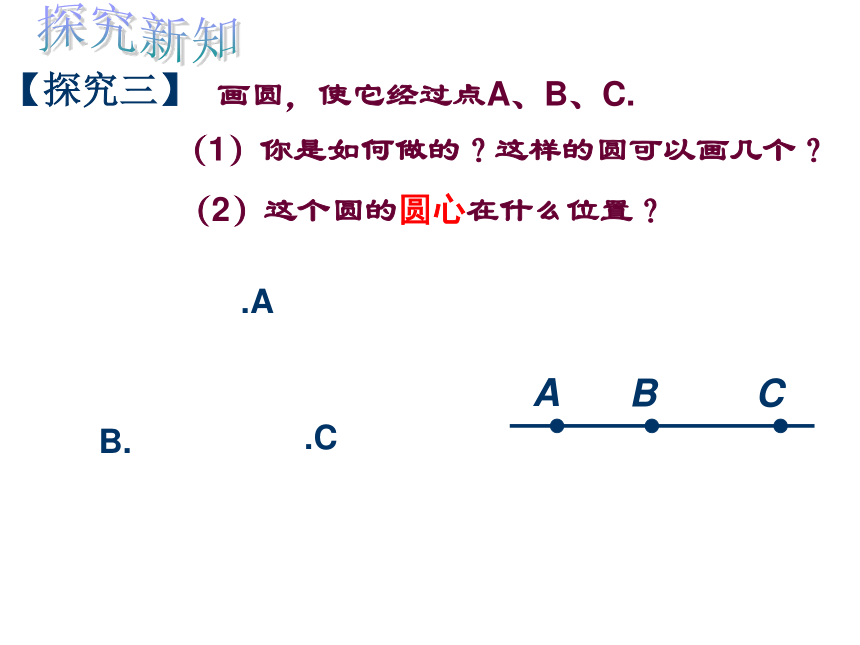
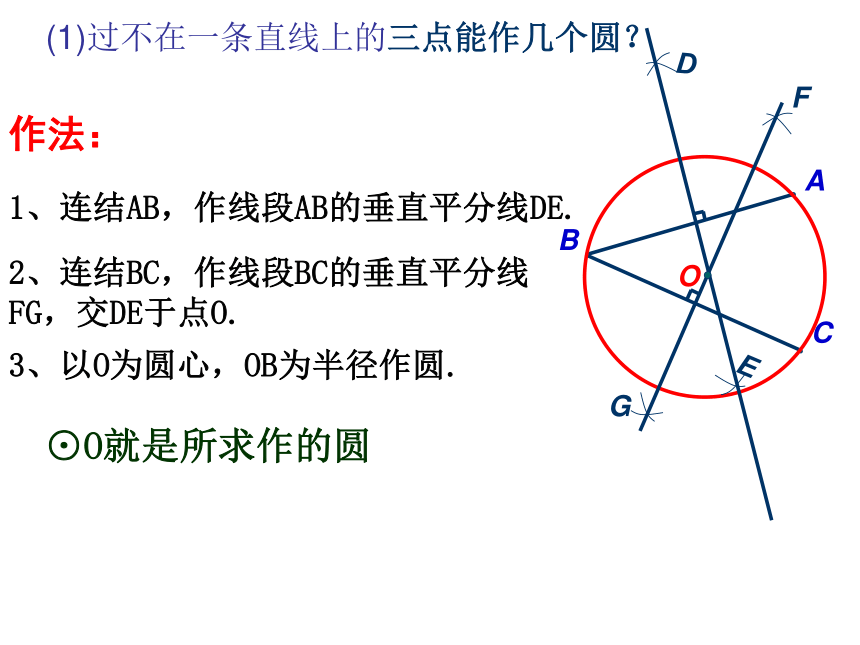
这点到A或B的距离为半径作圆.探究新知【探究三】画圆,使它经过点A、B、C.(2)这个圆的圆心在什么位置?(1)你是如何做的?这样的圆可以画几个?1、连结AB,作线段AB的垂直平分线DE.2、连结BC,作线段BC的垂直平分线 FG,交DE于点O.3、以O为圆心,OB为半径作圆.作法:⊙O就是所求作的圆(1)过不在一条直线上的三点能作几个圆?为什么过同一直线上的三点不能作圆呢?(2)过在同一直线上得三点能作几个圆?共线三点不能作圆反证法:(1)假设结论不成立。(2)推出矛盾。(与已知、定义、定理等)(3)得原结论成立。不在同一直线上的三点确定一个圆【归纳】经过三角形各顶点的圆叫做三角形的外接圆。
三角形外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。圆的内接三角形三角形的外接圆三角形的外心ABCO即时练习判断题:
1、过三点一定可以作圆 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边垂直平分线的交点 ( )
5、三角形的外心到三边的距离相等 ( )
6、等腰三角形的外心一定在这个三角形内( )×√×√××巩固新知 请分别画一个锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆,并观察外心的位置特点。及时小结这个三角形内部这个三角形外部斜边的中点巩固新知 用反证法证明:“两直线平行,同位角相等”例1 如图是一个破残的圆形轮片。
(1)求作此破残轮片所在圆的圆心(不写作法,保留作图痕迹)。(2)若弦AB 的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=24cm,CD=8cm。
求此破残轮片所在圆的半径。应用新知1、 A、B、C为三个不在一条直线上的村庄, 现欲建一个车站,使它到三个村庄的距离相等,则这个车站应建在何处?
A . .B
.C
自主练习2、如图,CD所在的直线垂直平分线段AB,怎样使用这样的工具找到圆形工件的圆心?自主练习理解提高1、经过四个点是不是一定能作圆?举例说明。
2 如果直角三角形的两条直角边分别是6cm,8cm,
则它的外接圆的半径是多少?理解提高3 已知直线ι及直线外两点A、B,
求作经过A、B两点且圆心在直线上ι的圆。例2.如图,在等腰△ABC中, 顶角∠A=120 °,
BC=12cm。
试求这个三角形的外接圆的半径.理解提高我学会了什么 ?过两点可以作无数个圆.圆心在以已知两点为端点的线段的垂直平分线上.实际问题过一点可以作无数个圆过三点过不在同一条直线上的三点确定一个圆过在同一直线上的三点不能作圆外心、三角形外接圆、圆的内接三角形外心、三角形外接圆、圆的内接三角形今天作业1 作业本(1)课时作业本 P84---85其余题
课堂小结2 会画三角形的外接圆。3 掌握三角形外心的确定方法,外心的位置,
外心的特点。1 理解不在同一直线上得三点确定一个圆。4 了解反证法的一般步骤,会用反证法证明一些简单问题。【探究三】 思考:1 平行四边形有外接圆吗?如果平行四边形有外接圆,
则这个平行四边形是哪种特殊的四边形?
圆心在哪里?【练一练】在同一平面内,已知a∥ b,c与a相交,用反证法证明:c与a相交。例2 用反证法证明:
三角形内角中至少有一个角不大于60°
(2)这些圆的圆心有何特点?探究新知【探究二】(1)这样的圆可以画几个?你是如何做的?(1)无数个
以线段AB的垂直平分线上的任意一点为圆心,
这点到A或B的距离为半径作圆.探究新知【探究三】画圆,使它经过点A、B、C.(2)这个圆的圆心在什么位置?(1)你是如何做的?这样的圆可以画几个?1、连结AB,作线段AB的垂直平分线DE.2、连结BC,作线段BC的垂直平分线 FG,交DE于点O.3、以O为圆心,OB为半径作圆.作法:⊙O就是所求作的圆(1)过不在一条直线上的三点能作几个圆?为什么过同一直线上的三点不能作圆呢?(2)过在同一直线上得三点能作几个圆?共线三点不能作圆反证法:(1)假设结论不成立。(2)推出矛盾。(与已知、定义、定理等)(3)得原结论成立。不在同一直线上的三点确定一个圆【归纳】经过三角形各顶点的圆叫做三角形的外接圆。
三角形外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。圆的内接三角形三角形的外接圆三角形的外心ABCO即时练习判断题:
1、过三点一定可以作圆 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边垂直平分线的交点 ( )
5、三角形的外心到三边的距离相等 ( )
6、等腰三角形的外心一定在这个三角形内( )×√×√××巩固新知 请分别画一个锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆,并观察外心的位置特点。及时小结这个三角形内部这个三角形外部斜边的中点巩固新知 用反证法证明:“两直线平行,同位角相等”例1 如图是一个破残的圆形轮片。
(1)求作此破残轮片所在圆的圆心(不写作法,保留作图痕迹)。(2)若弦AB 的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=24cm,CD=8cm。
求此破残轮片所在圆的半径。应用新知1、 A、B、C为三个不在一条直线上的村庄, 现欲建一个车站,使它到三个村庄的距离相等,则这个车站应建在何处?
A . .B
.C
自主练习2、如图,CD所在的直线垂直平分线段AB,怎样使用这样的工具找到圆形工件的圆心?自主练习理解提高1、经过四个点是不是一定能作圆?举例说明。
2 如果直角三角形的两条直角边分别是6cm,8cm,
则它的外接圆的半径是多少?理解提高3 已知直线ι及直线外两点A、B,
求作经过A、B两点且圆心在直线上ι的圆。例2.如图,在等腰△ABC中, 顶角∠A=120 °,
BC=12cm。
试求这个三角形的外接圆的半径.理解提高我学会了什么 ?过两点可以作无数个圆.圆心在以已知两点为端点的线段的垂直平分线上.实际问题过一点可以作无数个圆过三点过不在同一条直线上的三点确定一个圆过在同一直线上的三点不能作圆外心、三角形外接圆、圆的内接三角形外心、三角形外接圆、圆的内接三角形今天作业1 作业本(1)课时作业本 P84---85其余题
课堂小结2 会画三角形的外接圆。3 掌握三角形外心的确定方法,外心的位置,
外心的特点。1 理解不在同一直线上得三点确定一个圆。4 了解反证法的一般步骤,会用反证法证明一些简单问题。【探究三】 思考:1 平行四边形有外接圆吗?如果平行四边形有外接圆,
则这个平行四边形是哪种特殊的四边形?
圆心在哪里?【练一练】在同一平面内,已知a∥ b,c与a相交,用反证法证明:c与a相交。例2 用反证法证明:
三角形内角中至少有一个角不大于60°
同课章节目录
